Гистограмма и полигон распределения случайной величины

Статистическое исследование точности деталей, обработанных на настроенном станке

 

Разработал К.Г. Щетникович

 

 

Минск 2003

Лабораторная работа № 1

 

СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ТОЧНОСТИ ДЕТАЛЕЙ, ОБРАБОТАННЫХ НА НАСТРОЕННОМ СТАНКЕ

 

Цель работы

Овладеть методикой построения экспериментальной и теоретической кривых распределения размеров деталей, обработанных на настроенном станке, и определить вероятное количество годных и бракованных деталей.

 

Задачи работы

 

2.1. Усвоить последовательность построения гистограммы и полигона распределения размеров деталей в партии.

2.2. Ознакомиться с законами распределения размеров обрабатываемых заготовок и свойствами кривой Гаусса.

2.3. Построить теоретическую кривую распределения размеров деталей в партии.

2.4. Определить вероятный процент брака генеральной совокупности деталей по результатам измерений выборки.

2.5. Дать оценки точности обработки и оценить точность настройки станка на размер.

 

Инструмент, материалы и принадлежности

 

1. Партия обработанных деталей (40-50 шт.).

2. Головка рычажно-зубчатая 1ИГ, ГОСТ 18833-73.

3. Стойка С-III ГОСТ 10197-70.

4. Чертеж детали.

 

Теоретическая часть

Гистограмма и полигон распределения случайной величины

Все погрешности, возникающие при механической обработке, могут быть сведены к трем видам:

1) систематические постоянные;

2) систематические переменные;

3) случайные.

Систематические постоянные погрешности – это такие, величина которых остается постоянной у каждой детали партии. Причиной возникновения таких погрешностей являются, например, неточность настройки станка на заданный размер, износ станка и другие.

 

Систематические переменные погрешности также имеются у каждой детали партии, но их величина меняется по какой-либо закономерности. Источниками возникновения этих погрешностей могут быть, например, размерный износ инструмента, температурные деформации системы СПИД и др.

Случайные погрешности появляются в результате действия
одного или нескольких факторов, которые сами подвержены колебаниям случайного характера. Источниками случайных погрешностей могут
быть, например, колебания твердости и припусков у деталей данной партии.

С помощью методов математической статистики и теории вероятностей можно по результатам измерений части деталей (выборки) определить закон распределения размеров деталей сколь угодно большой партии (генеральной совокупности), обработанной на данном станке. Этот закон распределения будет учитывать величину и вероятность возникновения случайных погрешностей.

Многочисленными исследованиями показано, что в большинстве случаев распределение размеров деталей при обработке их на настроенном станке происходит по закону нормального распределения
случайных величин (закон Гаусса). Кривая нормального распределения описывается уравнением, которое будет приведено ниже. Анализ
параметров этого уравнения позволяет оценивать точность обработки
деталей, правильность настройки станка на размер, прогнозировать
ожидаемую точность и возможный процент брака большого количества деталей
по результатам измерений выборочной партии. Покажем это на примере.

У детали задан наружный диаметр

D = 30_–0,12 (D_max = 30,00; D_min = 29,88; D _ср = 29,94; IТ = 0,12).

Случайная выборка из партии в количестве n = 24 шт. была
измерена. Результаты измерений показали, что детали имеют мини-
мальный размер, равный 29,86 мм, и максимальный размер, равный
30,00 мм.

Разница между максимальным и минимальным размерами называется размахом:

ω = 30,00 – 29,86 = 0,14 мм.

Разобьем величину размаха на несколько интервалов (примем число интервалов равным 7). Тогда размер интервала будет равен 0,02 мм.

Количество деталей, попадающих в данный интервал размеров, называется частотой К.

Внесем полученные данные в таблицу.

Предположим, что частоты К оказались следующими (табл. 1).

 

Таблица 1. Результаты измерений партии деталей

Номер интервала	Интервал	Середина интервала	Частота (количество деталей в интервале)
	29,86-29,88	29,87
	Св. 29,88-29,90	29,89
	Св. 29,90-29,92	29,91
	Св. 29,92-29,94	29,93
	Св. 29,94-29,96	29,95
	Св. 29,96-29,98	29,97
	Св. 29,98-30,00	29,99

n = ∑ = 24

 

По полученном значениям можно найти среднее арифметическое значение размера (средний размер деталей в партии):

(1)

Следует учесть, что средний размер деталей в партии отличается от среднего значения размера, найденного по размаху. И действительно, это значение будет:

Имеем .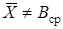

В данном примере эта разница невелика, но в других случаях она может быть и значительной.

Для наглядности по найденным результатам построим эмпирическую кривую распределения (рис. 1).

В координатной сетке по оси абсцисс отложим значения интервалов размера х, а по оси ординат частоты K_i, то есть количества деталей, попадающих в тот или иной интер­вал (данные из табл. 1). В результате построения получим фигуру, состоящую из вертикальных столбиков, которая назы­вается гистограммой распределения. Проведя ломаную через середины вершин столбиков, получим ломаную, называемую полигоном распределения случайной величины х.

На график нанесем все заданные и найденные значения: D_max, D _ср, D_min, IТ – заданные значения величин; ω, 1/2 ω, В _ср, – найденные значения.

Из сравнения нанесенных величин видно, что в данной выборке имеются детали, лежащие вне заданных значений D = 30_–0,12. Это детали первого интервала с размерами от 29,86 до 29,88 в количестве 2 шт. (К = 2). Так как размер этих деталей менее нижнего предела, следовательно, брак неисправный. Определим процент брака:

 

 

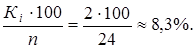
Рис. 1. График распределения случайной величины

 

Из рис. 1 видно, что площади гистограммы и полигона равны и соответствуют величине

S = (D xK ₁ + D xK ₂ + … + D xK_i) = D x (K ₁ + K ₂ + … + K_i) = .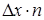

Если в формуле, определяющей процент брака, числитель и знаменатель умножить на D x, тогда получим

где S ₁ – площадь полигона, выходящая за пределы допуска; S – площадь всего полигона.

Следовательно, процент брака мог быть найден как отно­шение площади полигона (гистограммы), выходящей за пределы допуска IТ, ко всей площади полигона.

Гистограммы распределения партии деталей из п штук могут иметь различную форму. На рис.2 представлены для примера две возможные формы гистограмм.

 

 

Рис. 2. Возможные графики распределения случайной величины

Несмотря на то, что в обеих партиях число деталей одинаково, а следовательно, и площади одинаковы, несмотря на равенство размахов ω₁ и ω₂ и равенство , эти партии не равноценны по точности. У первой партии большое количество деталей находится у крайних пределов и возможен выход этих деталей из поля допуска, у второй партии, наоборот, детали тесно группируются у размера (центра группирования), и выход за пределы допуска маловероятен. Технологический процесс, по которому была обработана вторая партия деталей, более надежен и брак будет менее вероятным.

Рассмотренные ранее характеристики , ω не дают возможности оценить плотность группирования размеров деталей около значения , что очень важно для оценки качества технологического процесса и вероятности возникновения брака. Характеристикой, которая может дать такую оценку, является среднеквадратическое отклонение от среднего значения , которое вычисляется по следующей формуле:

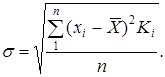
(2)

Величина среднеквадратического отклонения оценивает форму кривой распределения и фактически дает харак­теристику того, какие количества величин х и на каких расстояниях отстоят от величины . Так, например, для показанной на рис. 2, а кривой распределения, величина , подсчитанная по формуле (2), дает значение

= 0,038 мм,

а для кривой распределения на рис. 2, б

= 0,025 мм.

Размерность совпадает с размерностью случайной величины х (в нашем примере мм).

Для оценки генеральной совокупности по результатам оценки выборочной партии необходимо эмпирическую кривую распределения заменить теоретической кривой.