Означення. Диференціальним рівнянням з відокремлюваними змінними називається рівняння вигляду
 (4.1)
(4.1)
Порівняно із загальним виглядом рівняння першого порядку 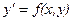 маємо
маємо
 . Далі маємо
. Далі маємо  , або
, або
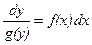 (4.2)
(4.2)
Якщо  вважати функцією від
вважати функцією від  , то маємо рівняння двох диференціалів, тому їх первісні відрізняються на довільну сталу. Інтегруючи рівність (4.2), одержимо загальний інтеграл диференціального рівняння
, то маємо рівняння двох диференціалів, тому їх первісні відрізняються на довільну сталу. Інтегруючи рівність (4.2), одержимо загальний інтеграл диференціального рівняння
 (4.3)
(4.3)
Зауваження. Диференціальне рівняння з відокремлюваними змінними можна подати у вигляді
 , де
, де 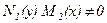 . Тепер маємо
. Тепер маємо  .Це рівняння з відокремленими змінними. Інтегруючи, знайдемо загальний інтеграл диференціального рівняння.
.Це рівняння з відокремленими змінними. Інтегруючи, знайдемо загальний інтеграл диференціального рівняння.
Приклад. Знайти частинний розв`язок рівняння
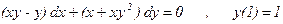
Зробимо перетворення

і відокремимо змінні (поділивши обидві частини рівняння на  ):
):

зінтегрувавши рівняння, одержимо
 ,
,
або

Визначимо з початкових умов довільну сталу:
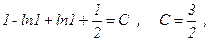
а потім, підставивши знайдене значення довільної сталої у загальний інтеграл, знайдемо шуканий частинний інтеграл
 або
або 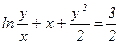
Однорідні рівняння першого порядку.
Означення 1. Функція  називається однорідною функцією
називається однорідною функцією  -го виміру, якщо для будь-якого
-го виміру, якщо для будь-якого  має місце тотожність
має місце тотожність

Приклади. Функція  - однорідна функція виміру
- однорідна функція виміру  , тому що
, тому що

Функція  - однорідна функція нульового виміру, тому що
- однорідна функція нульового виміру, тому що
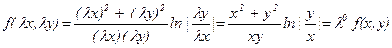
Означення 2. Диференціальне рівняння першого порядку
 (5.1)
(5.1)
називається однорідним, якщо функція  є однорідною функцією нульового виміру.
є однорідною функцією нульового виміру.
Розв`язання однорідного рівняння. Однорідна функція нульового виміру залежить лише від відношення змінних, бо  і якщо покласти
і якщо покласти  , то
, то  . Позначимо
. Позначимо  . Тоді рівняння (5.1) набуває вигляду
. Тоді рівняння (5.1) набуває вигляду
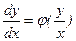 (5.2)
(5.2)
Зробимо підстановку  або
або  . Тоді маємо
. Тоді маємо 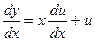 . Підставимо значення похідної в (5.2) і одержимо
. Підставимо значення похідної в (5.2) і одержимо 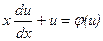 або
або  .
.
Ми одержали рівняння з відокремлюваними змінними. Вважаємо, що 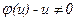 , і відокремлюємо змінні
, і відокремлюємо змінні 
 звідки
звідки  . Підставимо після інтегрування замість
. Підставимо після інтегрування замість  і знайдемо загальний інтеграл диференціального рівняння.
і знайдемо загальний інтеграл диференціального рівняння.
Зауваження. Рівняння  є однорідним, якщо функції
є однорідним, якщо функції  і
і  є однорідними функціями одного виміру.
є однорідними функціями одного виміру.
Приклад. Розв`язати рівняння  ,
, 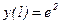
Це рівняння є однорідним тому, що  - однорідна функція нульового виміру: - однорідна функція нульового виміру:
- однорідна функція нульового виміру: - однорідна функція нульового виміру:
 . Покладемо
. Покладемо 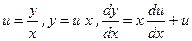 . Тоді після підстановки у рівняння, одержимо рівняння з відокремлюваними змінними:
. Тоді після підстановки у рівняння, одержимо рівняння з відокремлюваними змінними:

 або
або  .
.
Відокремлюючи змінні, знаходимо
 або
або  .
.
Зінтегрувавши, одержимо
 або
або  .
.
Підставивши  , отримаємо
, отримаємо
 , або
, або  , або
, або  .
.
Знаходимо шуканий частинний розв`язок з початкових умов
 , звідки
, звідки  або
або 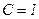 . Підставимо у загальний розв`язок
. Підставимо у загальний розв`язок 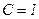 і добудемо шуканий частинний розв`язок, який задовольняє початковим умовам:
і добудемо шуканий частинний розв`язок, який задовольняє початковим умовам:





