Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника

 

 

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90^º и/или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 2.24). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник.

 

а) б)

Рисунок 2.24

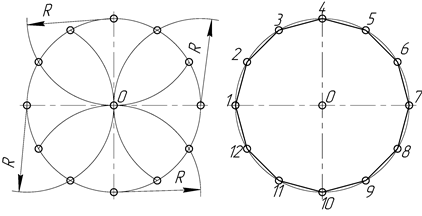
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 2.25). Соединив полученные точки, получают двенадцатиугольник.

 

а) б)

Рисунок 2.25

 

 

2.2.5 Деление окружности на пять и десять равных частей
и построение правильного вписанного пятиугольника и десятиугольника

 

 

Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 2.26.

 

а) б) в) г)

 

Рисунок 2.26

Половину любого диаметра (радиус) делят пополам (рис. 2.26 а), получают точку А.Из точки А,как из центра, проводят дугу радиусом, равным расстоянию от точки Адо точки 1 до пересечения со второй половиной этого диаметра, в точке В(рис. 2.26 б ). Отрезок 1Вравен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности. Делая засечки на окружности (рис. 2.26, в ) радиусом К,равным отрезку 1В,делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5 (рис. 2.26, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем. Если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 2.26, г).

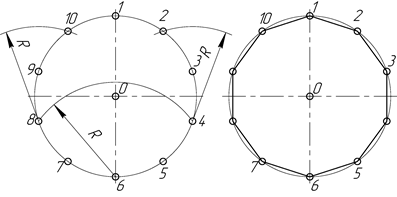
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 2.26), но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 2.27, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник(рис. 2.27, б).

 

а) б)

Рисунок 2.27

2.2.6 Деление окружности на семь и четырнадцать равных
частей и построение правильного вписанного семиугольника и
четырнадцатиугольника

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 2.28 и 2.29.

Из любой точки окружности, например точки А, радиусом заданной окружности проводят дугу (рис. 2.28, а ) до пересечения с окружностью в точках В и D. Соединим точки Ви Dпрямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС,делают засечки на окружности в последовательности, показанной на рис. 2.28, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 2.28, в).

Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 2.29, а).

 

а) б) в)

Рисунок 2.28

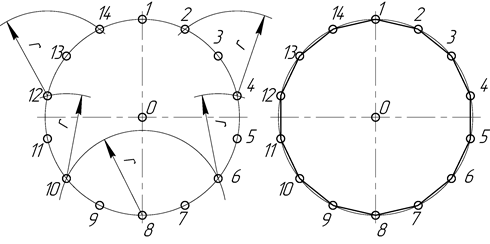
Сначала окружность делится на семь равных частей от точки 1, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырнадцатиугольник (рис. 2.29, б).

 

а) б)

Рисунок 2.29

 

 

Построение эллипса

 

 

Изображение окружности в прямоугольной изометрической проекции во всех трех плоскостях проекций представляет собой одинаковые по форме эллипсы.

Направление малой оси эллипса совпадает с направлением аксонометрической оси, перпендикулярной той плоскости проекций, в которой лежит изображаемая окружность.

При построении эллипса, изображающего окружность небольшого диаметра, достаточно построить восемь точек, принадлежащих эллипсу (рис. 2.30). Четыре из них являются концами осей эллипса (A, B, С, D),а четыре других (N₁, N_2, N_3, N₄) расположены на прямых, параллельных аксонометрическим осям, на расстоянии, равном радиусу изображаемой окружности от центра эллипса.

 

а	б

Рисунок 2.30