1) Непрерывность и равномерная непрерывность функций одной и двух переменных.
Теорема Кантора о равномерной непрерывности.
2) Непрерывность собственного интеграла 
по параметру.
3) Непрерывность интеграла 
по параметру.
4) Дифференцирование интеграла по параметру. Правило Лейбница.
5) Дифференцирование интеграла по параметру.
6) Интегрирование собственного интеграла по параметру.
7) Сходимость и равномерная сходимость несобственного интеграла, зависящего от параметра. Примеры равномерно и неравномерно сходящихся несобственных интегралов.
8) Признак Вейерштрасса равномерной сходимости несобственных интегралов.
9) Критерий Коши равномерной сходимости несобственных интегралов. Отрицание критерия Коши.
10) Непрерывность несобственного интеграла по параметру.
11) Интегрирование несобственного интеграла по параметру.
12) Интеграл Дирихле 
. Интеграл Эйлера-Пуассона 
.
13) Дифференцирование несобственного интеграла по параметру.
14) Интегралы Фруллани 
.
15) Интеграл Лапласа 
.
16) Теорема о перестановке двух несобственных интегралов.
17) Интегралы Френеля 
.
18) Интеграл Фурье как предельный случай ряда Фурье.
19) Признак Дини сходимости интеграла Фурье.
20) Преобразование Фурье. Свойства преобразования Фурье. Косинус-преобразование Фурье. Синус-преобразование Фурье.
21) Определение Гамма-функции как несобственного интеграла. Область сходимости соответствующего интеграла. Свойства Гамма-функции.
22) Производная от Гамма-функции и область сходимости соответствующего ей несобственного интеграла.
23) Бета-функция. Определение и основные свойства.
24) Эллиптические интегралы 1-го и 2-го рода в форме Лежандра. Полные эллиптические интегралы. Задачи, приводящие к эллиптическим интегралам (задача о математическом маятнике, задача о вычислении длины дуги эллипса).
25) Представление полных эллиптических интегралов в виде степенных рядов.
26) Дифференциальное уравнение Бесселя. Функции Бесселя 1-го рода.
27) Линейная зависимость функций 
при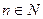 
. Определение функций Бесселя 2-го рода.
28) Свойства функций Бесселя 1-го рода.
29) Ортогональность функций Бесселя.
30) Многочлены Лежандра как собственные функции задачи Штурма-Лиувилля.
31) Свойства многочленов Лежандра.
32) Производящая функция многочленов Лежандра. Вывод рекуррентных соотношений с помощью производящей функции.
33) Системы ортогональных многочленов. Метод их получения. Основные свойства.
34) Многочлены Эрмита и их основные свойства (ортогональность, рекуррентные соотношения, производящая функция, дифференциальные уравнения, решениями которых они являются).
Задачи к зачету по дисциплине «Комплексный анализ»
