Образующийся на фильтровальной перегородке осадок представляет собой пористый слой, состоящий из, множества сообщающихся между собой пор (каналов) переменного сечения и кривизны. Поскольку частицы осадка обычно мелкие, поры между ними имеют небольшие размеры, поэтому полагают, что движение жидкости в них ламинарное. В простейшем виде можно представить что слой осадка состоит из пор одинакового диаметра и длины, равной высоте слоя осадка.
Зависимость между основными величинами, характеризующими гидравлическое сопротивление зернистого слоя при фильтровании (подобном движению жидкости в трубах и каналах), можно выразить известным из гидравлики уравнением Дарси:
,
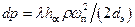где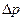 
– перепад давлений при фильтровании или гидравлическое сопротивление слоя осадка; 
– коэффициент сопротивления зернистого слоя; 
– высота слоя осадка;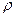 
– плотность жидкости (фильтрата); 
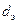– эквивалентный диаметр пор осадка; 
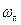– скорость жидкости в порах.
При ламинарном режиме движения жидкости в порах, когда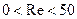 
, коэффициент сопротивления находится по зависимости:
,
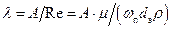где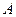 
– постоянная величина, равная 133–200.
С учетом значения уравнение примет вид:
.
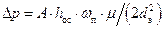Обозначив через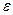 
порозность слоя, выражают скорость движения жидкости в порах 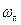через скорость 
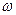, отнесенную ко всему сечению слоя, соотношением:
,
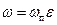откуда:
.
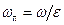Значение пор 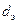определяют по формуле:
,
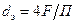где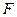 
– площадь сечения пор; 
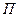– смоченный периметр пор.
Умножив числитель и знаменатель в выражении на , получим:
,
где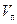 
– объем пор; 
– площадь их поверхности.
Так как объем пор в единице объема 
, а их поверхность равна удельной поверхности 
, то из формулы получают:
.
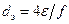Эквивалентный диаметр 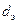можно выразить также через размер частиц, составляющих слой. Если слой состоит из сферических частиц диаметром 
, то поверхность одной частицы составит 
, а ее объем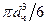 
. Тогда число частиц 
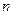в единице объема слоя равно отношению объема 
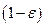, занятого частицами, к объему одной частицы, т. е.:
,
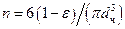а поверхность всех частиц:
.
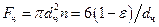Следовательно, эквивалентный диаметр пор:
.
Для несферических частиц вводят коэффициент формы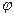 
, равный отношению поверхности 
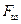шара того же объема, что и частица, к поверхности 
частицы (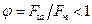
). Тогда:
.
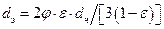После подстановки значени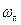й и 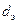в уравнение и обозначив произведение всех постоянных величин через 
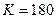, получают следующую формулу Кармана:
.
Формула Кармана широко применяется для определения гидравлического сопротивления, возникающего при движении жидкости через зернистый и пористый слой.
