Методика расчета линейных цепей при периодических
Несинусоидальных токах
Возможность разложения периодических несинусоидальных функций в ряд Фурье позволяет свести расчет линейной цепи при воздействии на нее несинусоидальных напряжений источников к расчету цепей с постоянными и синусоидальными токами в отдельности для каждой гармоники.
Мгновенные значения искомых токов и напряжений определяются на основе принципа наложения путем суммирования найденных при расчете гармонических составляющих напряжений и токов.
В соответствии с вышесказанным цепь на рис. 1 при воздействии на нее несинусоидальной ЭДС
(при расчете спектр рассматриваемых гармоник ограничивается количеством составляющих n) в расчетном плане представляется суммой цепей на рис. 2. 
Здесь 
.
Тогда, например, для тока в ветви с источником ЭДС, имеем
,
где каждая к-я гармоника тока рассчитывается символическим методом по своей k-й расчетной схеме. При этом для всех гармоник параметры 
и С постоянны.
;
.
Необходимо помнить, что ввиду различия частот суммировать комплексы различных гармоник недопустимо.
Таким образом, методика расчета линейных цепей при несинусоидальных токах сводится к следующему:
1. ЭДС и токи источников раскладываются в ряды Фурье.
2. Осуществляется расчет цепи в отдельности для постоянной и каждой гармонической составляющей.
3. Искомые величины определяются как алгебраические суммы соответствующих постоянной и гармонических составляющих.
Алгоритм расчета
1. Заданное аналитическое выражение периодического несинусоидального напряжения (ЭДС, тока) раскладываем в ряд Фурье в амплитудно-фазовой форме записи (можно и в тригонометрической форме)
где k – номер гармоники.
2. Каждую гармонику напряжения (ЭДС, тока) записываем в комплексной форме 
.
3. Для каждой гармоники определяем (в зависимости от выбранного метода расчета) комплексное сопротивление или комплексную проводимость
4. Для каждой гармоники напряжения (ЭДС, тока) находим комплексную амплитуду тока 
.
5.
5. Записываем выражение для мгновенного значения тока для каждой гармоники в отдельности. Мгновенное значение периодического несинусоидального тока получают, суммируя мгновенные значения всех гармонических составляющих токов:
Расчёт электрических цепей периодического несинусоидального тока путём использования принципа наложения справедлив только для линейных электрических цепей!!!!
3. Пример расчёта мгновенных значений токов на основе метода наложения
Рассмотрим расчёт линейных электрических цепей, находящихся под несинусоидальным напряжением. Допустим, что к цепи, состоящей из последовательно соединенных активного сопротивления R, индуктивности L и емкости С (рис. 3) приложено синусоидальное напряжение
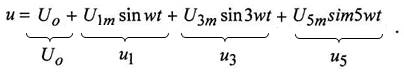
Рис. 3 Рис. 4
Из уравнения видно, что несинусоидальное напряжение содержит постоянную составляющую Uo и нечётные гармоники u1 u3, u5 (рис. 4).
Известно, что напряжение источников электроэнергии при их последовательном соединении складываются.
Поэтому данный источник электроэнергии с несинусоидальным напряжением можно заменить рядом последовательно соединенных источников (рис. 5).
 |
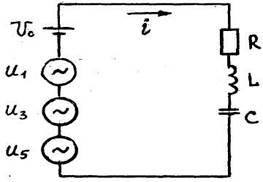Рис. 5.
Первый из них создает напряжение Uo, а второй, третий и четвёртый -синусоидальные напряжения:
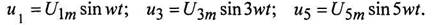
Соответственно с частотами w, 3 w, 5 w.
Каждой гармонике напряжения соответствует своя гармоника тока. Первая гармоника напряжения u1 создаёт первую гармонику тока i1, третья гармоника напряжения u3 - третью гармонику тока i3 и т.д. Постоянное напряжение Uo создаёт постоянный ток I0. Значение каждого тока зависит не только от значения соответствующего напряжения, но и от полного сопротивления цепи. Ток на каждом участке цепи определяется по принципу наложения путём суммирования токов, создаваемых каждым из слагаемых напряжения в отдельности:
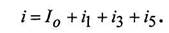
Следовательно, расчёт линейной цепи с несинусоидальным напряжением (ЭДС) сводится к решению нескольких задач. Определение одной постоянной составляющей и ряда синусоидальных составляющих тока, число которых равно числу синусоидальных составляющих напряжения (ЭДС).
3.1.Расчёт сопротивлений цепи для различных составляющих несинусоидального тока
При рассмотрении данного вопроса важно заметить, что сопротивления реактивных элементов для разных гармоник ток различны и зависят от частоты гармоники. Этот факт используется в электрических фильтрах.
Известно, что индуктивное и ёмкостное сопротивления для разных гармоник различны. С увеличением частоты f (или ω=2πf) индуктивное сопротивление 
увеличивается, а ёмкостное 
уменьшается. Поэтому для 
k-ой гармоники индуктивное сопротивление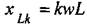 
, а ёмкостное
Определим полное сопротивление цепи (рис. 5) для каждой составляющей несинусоидального тока.
Для постоянной составляющей 
и полное сопротивление цепи Z0=∞.
Если в ветви цепи имеется конденсатор, то эта ветвь для постоянного тока представляет обрыв и постоянного тока в ней нет.
Полное сопротивление цепи для первой гармоники:
а для третьей и пятой
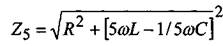
Из-за наличия реактивных элементов цепи угол сдвига по фазе между напряжением и током для каждой гармоники φk также будет различен и определяется по формуле:
Если задано уравнение несинусоидального напряжения и определены сопротивления, то по закону Ома можно определить амплитуды гармоник тока
Тогда с учётом угла сдвига по фазе между напряжением и током каждой гармоники можно записать выражение для тока в цепи:
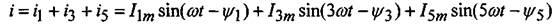
где ψik = ψuk - φk.- начальная фаза k-ой гармоники тока;
ψuk.- начальная фаза k-ой гармоники напряжения (в данном примере по исходным данным для всех гармоник напряжения она равна нулю).
Действующее значение и мощность несинусоидального тока
Действующее значение несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений токов всех гармонических составляющих:
Аналогично определяем действующее значение приложенного несинусоидального напряжения:
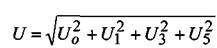
где 
;
-действующие значения гармонических составляющих напряжения.
Действующие значения несинусоидальных напряжений и токов показывают приборы электромагнитной и электродинамической систем.
Активная мощность цепи при несинусоидальном токе выражается формулой:
> где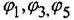 
- угол сдвига по фазе между одноименными гармониками напряжения и тока..
