1. Строение газообразных, жидких и твердых тел
Молекулярно-кинетическая теория дает возможность понять, почему вещество может находиться в газообразном, жидком и твердом состояниях.
Газы. В газах расстояние между атомами или молекулами в среднем во много раз больше размеров самих молекул (рис.8.5). Например, при атмосферном давлении объем сосуда в десятки тысяч раз превышает объем находящихся в нем молекул.
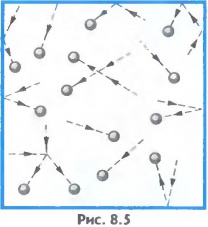
Газы легко сжимаются, при этом уменьшается среднее расстояние между молекулами, но форма молекулы не изменяется (рис.8.6).
Молекулы с огромными скоростями - сотни метров в секунду - движутся в пространстве. Сталкиваясь, они отскакивают друг от друга в разные стороны подобно бильярдным шарам. Слабые силы притяжения молекул газа не способны удержать их друг возле друга. Поэтому газы могут нео граниченно расширяться. Они не сохраняют ни формы, ни объема.
Многочисленные удары молекул о стенки сосуда создают давление газа.
Жидкости. Молекулы жидкости расположены почти вплотную друг к другу (рис.8.7), поэтому молекула жидкости ведет себя иначе, чем молекула газа. В жидкостях существует так называемый ближний порядок, т. е. упорядоченное расположение молекул сохраняется на расстояниях, равных нескольким молекулярным диаметрам. Молекула колеблется около своего положения равновесия, сталкиваясь с соседними молекулами. Лишь время от времени она совершает очередной «прыжок», попадая в новое положение равновесия. В этом положении равновесия сила отталкивания равна силе притяжения, т. е. суммарная сила взаимодействия молекулы равна нулю. Время оседлой жизни молекулы воды, т. е. время ее колебаний около одного определенного положения равновесия при комнатной температуре, равно в среднем 10-11 с. Время же одного колебания значительно меньше (10-12-10-13 с). С повышением температуры время оседлой жизни молекул уменьшается.
Характер молекулярного движения в жидкостях, впервые установленный советским физиком Я.И.Френкелем, позволяет понять основные свойства жидкостей.
Молекулы жидкости находятся непосредственно друг возле друга. При уменьшении объема силы отталкивания становятся очень велики. Этим и объясняется малая сжимаемость жидкостей.
Как известно, жидкости текучи, т. е. не сохраняют своей формы. Объяснить это можно так. Внешняя сила заметно не меняет числа перескоков молекул в секунду. Но перескоки молекул из одного оседлого положения в другое происходят преимущественно в направлении действия внешней силы (рис.8.8). Вот почему жидкость течет и принимает форму сосуда.
Твердые тела. Атомы или молекулы твердых тел, в отличие от атомов и молекул жидкостей, колеблются около определенных положений равновесия. По этой причине твердые тела сохраняют не только объем, но и форму. Потенциальная энергия взаимодействия молекул твердого тела существенно больше их кинетической энергии.
Есть еще одно важное различие между жидкостями и твердыми телами. Жидкость можно сравнить с толпой людей, где отдельные индивидуумы беспокойно толкутся на месте, а твердое тело подобно стройной когорте тех же индивидуумов, которые хотя и не стоят по стойке смирно, но выдерживают между собой в среднем определенные расстояния. Если соединить центры положений равновесия атомов или ионов твердого тела, то получится правильная пространственная решетка, называемая кристаллической.
На рисунках 8.9 и 8.10 изображены кристаллические решетки поваренной соли и алмаза. Внутренний порядок в расположении атомов кристаллов приводит к правильным внешним геометрическим формам.
На рисунке 8.11 показаны якутские алмазы.
У газа расстояние l между молекулами много больше размеров молекулr0:' l>>r0.
У жидкостей и твердых телl≈r0. Молекулы жидкости расположены в беспорядке и время от времени перескакивают из одного оседлого положения в другое.
У кристаллических твердых тел молекулы (или атомы) расположены строго упорядоченно.
2. Идеальный газ в молекулярно-кинетической теории
Изучение любой области физики всегда начинается с введения некой модели, в рамках которой идет изучение в дальнейшем. Например, когда мы изучали кинематику, моделью тела была материальная точка и т. д. Как вы уже догадались, модель никогда не будет соответствовать реально происходящим процессам, но часто она очень сильно приближается к этому соответствию.
Молекулярная физика, и в частности МКТ, не является исключением. Над проблемой описания модели работали многие учёные, начиная с восемнадцатого века: М. Ломоносов, Д. Джоуль, Р. Клаузиус (Рис. 1). Последний, собственно, и ввёл в 1857 году модель идеального газа. Качественное объяснение основных свойств вещества на основе молекулярно-кинетической теории не является особенно сложным. Однако теория, устанавливающая количественные связи между измеряемыми на опыте величинами (давлением, температурой и др.) и свойствами самих молекул, их числом и скоростью движения, весьма сложна. У газа при обычных давлениях расстояние между молекулами во много раз превышает их размеры. В этом случае силы взаимодействия молекул пренебрежимо малы и кинетическая энергия молекул много больше потенциальной энергии взаимодействия. Молекулы газа можно рассматривать как материальные точки или очень маленькие твердые шарики. Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать его модель – идеальный газ.
| 
| 
|
Рис. 1. Джеймс Джоуль, Михаил Ломоносов, Рудольф Клаузиус
Идеальный газ – модель газа, в рамках которого молекулы и атомы газа представлены в виде очень маленьких (исчезающих размеров) упругих шариков, которые не взаимодействуют друг с другом (без непосредственного контакта), а только сталкиваются (см. Рис. 2).
Следует отметить, что разреженный водород (под очень маленьким давлением) практически полностью удовлетворяет модели идеального газа.
Рис. 2.
Идеальный газ - это газ, взаимодействие между молекулами которого пренебрежимо мало. Естественно, при столкновении молекул идеального газа на них действует сила отталкивания. Так как молекулы газа мы можем согласно модели считать материальными точками, то размерами молекул мы пренебрегаем, считая, что объем, который они занимают, гораздо меньше объема сосуда.
Напомним, что в физической модели принимают во внимание лишь те свойства реальной системы, учет которых совершенно необходим для объяснения исследуемых закономерностей поведения этой системы. Ни одна модель не может передать все свойства системы. Сейчас нам предстоит решить довольно узкую задачу: вычислить с помощью молекулярно-кинетической теории давление идеального газа на стенки сосуда. Для этой задачи модель идеального газа оказывается вполне удовлетворительной. Она приводит к результатам, которые подтверждаются опытом.
3. Давление газа в молекулярно-кинетической теории Пусть газ находится в закрытом сосуде. Манометр показывает давление газа p0. Как возникает это давление?
Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с некоторой силой. В результате беспорядочных ударов о стенку давление быстро меняется со временем примерно так, как показано на рисунке 8.12. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента - мембраны. Несмотря на небольшие изменения давления, среднее значение давления p0 практически оказывается вполне определенной величиной, так как ударов о стенку очень много, а массы молекул очень малы.
Идеальный газ - модель реального газа. Согласно этой модели молекулы газа можно рассматривать как материальные точки, взаимодействие которых происходит только при их столкновении. Сталкиваясь со стенкой, молекулы газа оказывают на нее давление.
4. Микро- и макропараметры газа
Теперь можно приступить к описанию параметров идеального газа. Они делятся на две группы:
Параметры идеального газа
То есть микропараметры описывают состояние отдельно взятой частицы (микротела), а макропараметры – состояние всей порции газа (макротела). Запишем теперь соотношение, связывающее одни параметры с другими, или же основное уравнение МКТ:
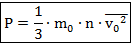
Здесь: 
- средняя скорость движения частиц;
Определение. 
– концентрация частиц газа – количество частиц, приходящихся на единицу объёма; 
; единица измерения – 
.
5. Среднее значение квадрата скорости молекул
Для вычисления среднего давления надо знать среднюю скорость молекул (точнее, среднее значение квадрата скорости). Это не простой вопрос. Вы привыкли к тому, что скорость имеет каждая частица. Средняя же скорость молекул зависит от движения всех частиц.
Средние значения. С самого начала нужно отказаться от попыток проследить за движением всех молекул, из которых состоит газ. Их слишком много, и движутся они очень сложно. Нам и не нужно знать, как движется каждая молекула. Мы должны выяснить, к какому результату приводит движение всех молекул газа.
Характер движения всей совокупности молекул газа известен из опыта. Молекулы участвуют в беспорядочном (тепловом) движении. Это означает, что скорость любой молекулы может оказаться как очень большой, так и очень малой. Направление движения молекул беспрестанно меняется при их столкновениях друг с другом.
Скорости отдельных молекул могут быть любыми, однако среднее значение модуля этих скоростей вполне определенное. Точно так же рост учеников в классе неодинаков, но его среднее значение - определенное число. Чтобы это число найти, надо сложить рост отдельных учеников и разделить эту сумму на число учащихся.
Среднее значение квадрата скорости. В дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости. От этой величины зависит средняя кинетическая энергия молекул. А средняя кинетическая энергия молекул, как мы вскоре убедимся, имеет очень большое значение во всей молекулярно-кинетической теории.
Обозначим модули скоростей отдельных молекул газа через 
. Среднее значение квадрата скорости определяется следующей формулой:
где N - число молекул в газе.
Но квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат ОХ, ОY, ОZ. Поэтому
Средние значения величин 
можно определить с помощью формул, подобных формуле (8.9). Между средним значением 
и средними значениями квадратов проекций существует такое же соотношение, как соотношение (8.10):
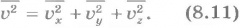
Действительно, для каждой молекулы справедливо равенство (8.10). Сложив такие равенства для отдельных молекул и разделив обе части полученного уравнения на число молекул N, мы придем к формуле (8.11).
Внимание! Так как направления трех осей ОХ, ОY и OZ вследствие беспорядочного движения молекул равноправны, средние значения квадратов проекций скорости равны друг другу:
Видите, из хаоса выплывает определенная закономерность. Смогли бы вы это сообразить сами?
Учитывая соотношение (8.12), подставим в формулу (8.11)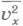 
вместо 
и 
. Тогда для среднего квадрата проекции скорости получим:
т. е. средний квадрат проекции скорости равен 1/3 среднего квадрата самой скорости. Множитель 1/3 появляется вследствие трехмерности пространства и соответственно существования трех проекций у любого вектора.
Скорости молекул беспорядочно меняются, но средний квадрат скорости вполне определенная величина.
6. Основное уравнение молекулярно-кинетической теории
Приступаем к выводу основного уравнения молекулярно-кинетической теории газов. В этом уравнении устанавливается зависимость давления газа от средней кинетической энергии его молекул. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.
Доказательство почти любого утверждения в физике, вывод любого уравнения могут быть проделаны с различной степенью строгости и убедительности: очень упрощенно, более или менее строго или же с полной строгостью, доступной современной науке.
Строгий вывод уравнения молекулярно-кинетической теории газов довольно сложен. Поэтому мы ограничимся сильно упрощенным, схематичным выводом уравнения. Несмотря на все упрощения, результат получится верный.
Вывод основного уравнения. Вычислим давление газа на стенку CD сосуда ABCD площадью S, перпендикулярную координатной оси OX (рис.8.13).
При ударе молекулы о стенку ее импульс изменяется: 
. Так как модуль скорости молекул при ударе не меняется, то 
. Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен 
.
Молекул много, и каждая из них передает стенке при столкновении такой же импульс. За секунду они передадут стенке импульс 
, где Z - число столкновений всех молекул со стенкой за это время. Число очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число Z пропорционально скорости молекул 
. Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки S: 
. Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с 
и полный импульс, переданный стенке за 1 с, равен:
Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равно действующей на него силе: 
.
Учтем, что не все молекулы имеют одно и то же значение квадрата скорости 
. В действительности средняя за секунду сила, действующая на стенку, пропорциональна не , а среднему квадрату скорости 
: 
. Так как согласно формуле (8.13) 
, то 
. Таким образом, давление газа на стенку сосуда равно:
Это и есть основное уравнение молекулярно-кинетической теории газов.
Формула (8.14) связывает макроскопическую величину - давление, кото-рое может быть измерено манометром, - с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.
Таким образом, основное уравнение МКТ вводит нам прямо пропорцио-нальную зависимость макропараметра давления от микропараметров массы молекулы и средней скорости движения в квадрате. То есть чем тяжелее частицы и чем больше их скорости, тем сильнее они врезаются в стенки сосуда и тем большее оказывают давление.
Возможны и другие формы записи этого уравнения, если вспомнить некоторые формулы из более ранних разделов физики:
- средняя кинетическая энергия поступательного движения
