Вопросы к экзамену по математике (1 семестр)
Элементы линейной алгебры
1. Матрицы и операции над ними.
2. Определители, их свойства и способы вычисления.
3. Обратная матрица.
4. Ранг матрицы и его вычисление.
5. Решение систем линейных уравнений по формулам Крамера.
6. Решение систем линейных уравнений матричным методом.
7. Теорема Кронекера-Капелли.
8. Решение систем линейных уравнений методом Гаусса.
9. Линейные однородные системы и их решение.
Векторная алгебра.
10. Векторы, линейные операции над векторами.
11. Линейная зависимость и независимость векторов. Базис на плоскости и в пространстве.
12. Координаты вектора. Направляющие косинусы вектора.
13. Линейные операции над векторами в координатной форме.
14. Скалярное произведение векторов, его свойства и применение.
15. Векторное произведение векторов, его свойства, применение.
16. Смешанное произведение векторов, его свойства и применение.
Элементы аналитической геометрии.
17. Преобразование системы координат.
18. Декартовая прямоугольная система координат на плоскости и в пространстве. Понятия уравнений линии и поверхности.
19. Прямая на плоскости. Угол между прямыми. Расстояние от точки до прямой.
20. Кривые 2-го порядка: окружность, эллипс, гипербола, парабола, их геометрические свойства, канонические уравнения.
21. Приведение общего уравнения кривой 2-го порядка к каноническому виду.
22. Плоскость в пространстве. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние от точки до плоскости.
23. Прямая в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
24. Плоскость и прямая в пространстве. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
25. Поверхности 2-го порядка.
Введение в математический анализ
26. Предел функции в точке и на бесконечности.
27. Бесконечно малые и бесконечно большие функции.
28. Свойства предела функции.
29. Два замечательных предела.
30. Применение эквивалентных бесконечно малых функций для вычисления пределов. Таблица эквивалентных бесконечно малых.
31. Числовая последовательность и её предел.
32. Непрерывность функции.
33. Точки разрыва и их классификация.
34. Свойства непрерывных функций.
35. Непрерывность основных элементарных функций.
Производная
36. Понятие производной, ее геометрический и механический смысл.
37. Непрерывность и дифференцируемость функции.
38. Производная постоянной, суммы, произведения и частного.
39. Производная сложной функции.
40. Производная обратной функции.
41. Производные основных элементарных функций.
42. Производная функции, заданной параметрически.
43. Производная функции, заданной неявно.
44. Логарифмическое дифференцирование.
45. Дифференциал функции, его свойства.
46. Производные высших порядков.
47. Дифференциалы высших порядков.
48. Теоремы о среднем.
49. Правило Лопиталя.
50. Формула Тейлора.
51. Признаки возрастания и убывания функции.
52. Экстремум функции.
53. Выпуклость и вогнутость функции, точки перегиба.
54. Асимптоты.
55. Общая схема исследования функции и построения ее графика.
56. Наибольшее и наименьшее значения функции на отрезке.
Задачи для подготовки к экзамену
(обязательно решить индивидуальное домашнее задание)
1.Вычислить определитель, используя метод Гаусса 
;
2. Решить систему с помощью правила Крамера 
;
3. Решить матричное уравнение 
;
4. Решить систему методом Гаусса 
;
5. Найти длину │AD│ -длину высоты ∆ABC, если А(2,3), В(-1,1), С(0,2). Написать уравнение прямой AD;
6. Верно ли, что точки: А(2,3,-1), В(-1,1,0), С(0,2,3), D(2,0,1) лежат в одной плоскости. Если да, то написать уравнение этой плоскости.
7. Определить тип кривой, заданной уравнением: 16x2-9y2-64x-54y-161=0. Найти ее центр и полуоси.
8. Написать уравнение плоскости, проходящей через точки А(2,3,-1), В(-1,1,0) перпендикулярно плоскости x+y-z+5=0;
9. Найти точки разрыва функции y= 
;
10. Вычислить 
;
11. Вычислить 
;
12. Вычислить 
.
13. Найти производную функции: 
14. Найти производную функции: 
15. Найти производную функции: 
16. Найти асимптоты к графику функции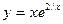 
;
- Найти промежутки выпуклости – вогнутости функции
; - Найти производную функций, заданных неявно:
- Найти производные функций, заданных параметрически:
- Найти производные второго порядка заданных функций:
; - Логарифмическое дифференцирование:
- Вычислить производную сложной функции:
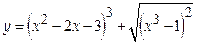
23. Вычислить производную сложной функции: 
- Вычислить пределы по правилу Лопиталя:
1. 
; 3. 
;
2. 
; 4. 
.
- Исследовать функцию на непрерывность, указать характер точек разрыва. Построить график функции:
а) 
; б) 
26. Вычислить определитель
27.Найти произведение двух матриц А и В (С=АВ) и обратную матрицу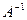 
28.Решить систему линейных алгебраических уравнений с помощью обратной матрицы или методом Гаусса
29. Даны координаты вершин призмы 
, 
, 
и 
.
Определить (или составить уравнение):
1. Плоскость, в которой расположена грань 
;
2. Уравнение прямой, на которой расположено ребро 
;
3. Угол между гранями и 
;
4. Угол между ребром и гранью ;
5. Уравнение прямой, на которой расположена высота из точки 
на грань ;
6. Расстояние от точки до грани :
7. Площадь грани ;
8. Объем пирамиды;
9. Точку пересечения высоты из вершины на плоскость грани ;
10. Угол между ребрами и 
.
I семестр
Контрольная работа 1 – «Линейная алгебра»
1. Найти 2ВТ – ВА, если 
.
2. Вычислить определитель: 
.
3. Решить систему уравнений матричным способом, выполнить проверку: 
4. При каком значении l матрицы 
и 
перестановочны?
5. Решить методом Гаусса систему уравнений, выполнить проверку. 
Контрольная работа 2–«Векторная алгебра и аналитическая геометрия»
1. Вычислить работу равнодействующей сил 
и 
, если ее точка приложения перемещается из начала координат в точку М(2,3,-1).
2. При каком значении a векторы 
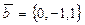и 
и 
будут компланарны?
3. Найти уравнение прямой, проходящей через точку М(2;1) параллельно прямой y=1,5x+4.
4. Написать уравнение плоскости, проходящей через точку А(-1,-1,6) и прямую 
5. Найти уравнение перпендикуляра из точки А(1;0;2) к плоскости 2x-y+3z-6=0.
6. Найти уравнение эллипса, если его малая ось равна 10, эксцентриситет 
, а фокусы лежат на оси абсцисс симметрично относительно начала координат.
Контрольная работа 3 – «Пределы и непрерывность функции»
1.Вычислить пределы
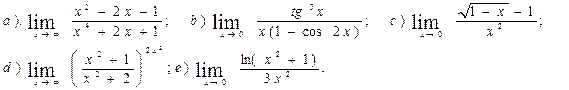
2. Исследовать функцию на непрерывность и построить схематический график: 
Контрольный опрос 1 – «Векторы»
1. Даны векторы: 
. Для каких векторов определена операция сложения? Выполните её.
2. Найдите длину вектора 
.
3. Дайте определение скалярного произведения векторов, запишите его свойства.
4. Запишите условия коллинеарности, перпендикулярности и компланарности векторов.
Контрольный опрос 2 – «Аналитическая геометрия»
1. Напишите уравнение прямой, проходящей через точку А(2; – 3; 5) параллельно вектору 
.
2. Напишите уравнение плоскости, проходящей через точку В(1; – 4; 0) пепендикулярно вектору 
.
3. Какие следующих прямых: а) параллельны; б) перпендикулярны? Почему?
.
4. Постройте кривые 2-го порядка:
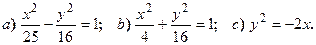
Варианты экзаменационного теста
1. Найти матрицу 
, если 
2. Дано: 
. Найти длину вектора 
3. Дан треугольник с вершинами А(-2;0), В(2;6) и С(4;2). Составить уравнения стороны АС, медианы ВД, высоты ВЕ.
4.Найти производную неявной функции: 
.
5.Исследовать на непрерывность и построить график функции: 
.
6.Определение обратной матрицы. Необходимое и достаточное условия существования обратной матрицы. Методика нахождения обратной матрицы.
1. Скалярное произведение векторов: определение, свойства, вычисление в координатной форме, основные задачи.
2. Решить систему методом Гаусса 
.
3. При каком значении 
вектора 
и 
коллинеарны, если 
, 
, где 
.
4. Найти уравнения прямой, проходящей через точку Р(1, 2, -2) перпендикулярно плоскости 3x + y – 2z – 4 = 0.
5. Вычислить 
.
6. Найти производную 
в точке 
: 
.
