Electrothermal ESD simulations of a 3D NMOS structure are presented to demonstrate the capabilities of TCAD for ESD. Figure 7 shows the structure of the NMOS simulated.Only half of the device has been modeled to save mesh points by taking advantage of the symmetry plane in the middle of the

«Fig. 7.». Three-dimensional NMOS structure simulated; the DCG has been varied
device. The gate length is 0.35 mm, and the entiresimulation area is 6.3 x 3.5 x 10 mm. The distance between the drain-contact and gate has been varied as indicated.
Figure 8 shows the typical snapback I–V characteristics during an ESD surge.

«Fig. 8.» (Top) Snapback I–V characteristics of 3D NMOS in logarithmic current scale and (bottom) linear current scale.
The structure with the smaller drain-contact to gate (DCG) spacing shows a lower resistivity in the high-current regime as expected. The important ESD quantities, snapback point, holding point, and Ron, are shown also in Figure 8. Even It2 can be identified by a sudden increase of the voltage due to current filament formation and the subsequent voltage drop when the silicon becomes intrinsic.
Figure 9 shows contour plots of the total current density and the temperature at six different current levels.

«Fig. 9.» Contour plots of total current density (upper six graphics) and temperature (lower six graphics) at the drain current level indicated.
The first picture, at Id = 3 x 10–4 A, shows the situation immediately before snapback. The breakdown occurs at the drain-to-bulk junction towards the gate. The impact ionization is homogeneous along the junction, indicated by the homogeneous current density. The picture at Id = 3.4 x 10–4 A is taken immediately after snapback. The parasitic NPN transistor triggers first in the middle of the device, which leads to an inhomogeneous current flow. At the holding point, Id = 3 x 10–3 A, the current flow is still inhomogeneous but starts to homogenize. The current constriction during snapback cannot be modeled with 2D device simulations. Therefore, 2D simulations would predict too low a holding voltage because a larger effective device width is assumed.
Above the holding point, the current starts to flow more and more homogeneously over the entire width of the device, and the temperature starts to rise. The hot spot lies at the drain junction towards the gate, and the temperature is higher in the middle of the device. This leads eventually to a destructive current filament in the middle of the device when the temperature approaches the intrinsic temperature of silicon.
In the last few years, the transient interferometric mapping (TIM) characterization technique from TU Vienna has proven to be invaluable in characterizing internal device behavior such as hot spots during highcurrent pulses [9].
The quantity measured in a TIM measurement is the phase shift of the laser probe beam. Only a qualitative comparison of the measured phase shift to simulation results (temperature, current density) has been possible. To compare TIM measurements directly to simulation results, the tool Absorption and Phase shift Extraction (APEX) was developed by Synopsys. APEX is a postprocessor that extracts the phase shift from Sentaurus Device results so that it can be compared to the measured phase shift directly. An advanced example showing the use of APEX is available from SolvNet [10].
Compact Modeling for ESD
There is a great need to include ESD compact models in circuit simulations to predict critical current paths and critical (I,V) node values, and to enhance input/output design quality [11]. The insight gained by TCAD permits developing physically based compact model add-ons for ESD. Internal device characteristics not accessible by measurements can be studied. Calibrated process and device simulation allows parameter extraction for ESD compact models. Expensive, noisy, and destructive measurements can be avoided.
To keep the compact model development effort to a reasonable level, a modular modeling strategy is chosen. This strategy is often referred to as macro-modeling or subcircuit modeling in the literature [12]. The standard model of the corresponding device (for example, a Gummel–Poon or BSIM model) has been retained for normal operation conditions, and it has been extended by ESDspecific add-on modules to form a full ESDcompact model.
The operational regime of devices under ESD stress is beyond the range in which standard compact models have been tested and verified; whereas, the full ESD compact models allow for reproducing behavior under ESD stress in circuit simulation. Thermal effects are included by establishing a feedback loop between electric and thermal domains. The thermal domain is modeled using first-order or higher-order thermal RC networks, depending on the complexity of the temperature fields of the device (one or more highly localized hot spots or almost homogeneous distribution). Figure 10 shows how the ESD compact models are set up.

«Fig. 10.». Modular setup of ESD compact models including thermal network fed by dissipated power Pel. The resulting temperatures T1…Tn complete the feedback loop.
A dedicated methodology for the extraction of ESD compact model parameters is developed, based on TCAD results and measurements.
The calibrated ESD compact models can be used within circuit simulations to determine critical current paths, to identify endangered devices, and to optimize protection circuitry. Circuit simulations with up to ten ESD protection devices and 100 standard devices are feasible. The limitation arises from the well-known convergence problems caused by the strong nonlinear behavior of the protection devices under ESD stress conditions and from their interaction with the rest of the circuit.
The nonlinearities cannot be eliminated, but they can be reduced to an acceptable level by giving particular attention to numeric issues. While nonlinear behavior (for example, snapback devices) is one key issue to account for in ESD simulations, it makes the numeric treatment extremely unstable and computing intensive. Nevertheless, the circuit complexity extends simple input/output pad protection configurations, including large parts of the internal circuit. For the implementation of the ESD add-on model equations, Verilog-A behavioral modeling language can be used. Verilog-A can be read by most common circuit simulators such as HSPICE® and Spectre.
Figure 11 shows an example of a protection NPN transistor ESD compact model.
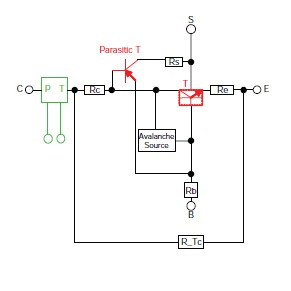
«Fig. 11.» Protection NPN transistor ESD compact model: (red) standard models, (black) ESD compact model add-ons, and (green) coupling to thermal network.
Current- and temperature-dependent series resistors account for conductivity modulation effects and self-heating, and are modeled externally. Thermal breakdown is modeled by R_Tc, which switches irreversibly from a very high to a very low Ohmic state at a critical temperature. The modeling of avalanche breakdown at the collector-base junction is the key element for simulating the snapback behavior. To eliminate the singularity at Vcb = BVcbo in the original Miller [13] formulation of the avalanche multiplication factor M, the method reported in [4] is followed, with an extension to account for weak avalanche current contribution. The resulting function is an approximation of the original M, but its value is limited at Vcb = BVcbo and it shows a significantly better convergence behavior.
Apart from the core transistor itself, the parasitic PNP between the source, collector, and base is included.
The transient triggering behavior [14] is influenced mainly by the junction capacitances (displacement current triggering), which cause a decreasing trigger voltage peak for increasing stress current rise-times, as well as by the base forward transit time (finite amount of time required by the carriers to traverse the base region leading to base-emitter diffusion capacitance), which reduces the triggering speed. Capacitances and base transit time as well as the current gain of the bipolar transistors, which determines the holding voltage Vh, are parameters belonging to the standard compact model instances. Their extraction is usually performed by simulations or measurements under normal operation conditions. Their values in the very diverse ESD current regimes may differ considerably compared to normal operation conditions. Therefore, a readjustment of these parameters may be necessary to obtain the correct behavior under ESD stress conditions.
ESD Circuit Simulation
In Figure 12, the ESD compact models for a protection NPN transistor and for two protection diodes are used within an input pin protection HBM circuit simulation.

«Fig.12.» Additional external base resistor Rbext increases the protection NPN triggering speed during an HBM stress simulation. Consequently, the effect of the D2 voltage overshoot peak on the voltage at the input node is reduced. Rbext also leads to a reduction of the holding voltage. Time axis is plotted in logarithmic scale to show the details of the protection NPN transistor triggering.
For simplicity, the internal circuitry comprising the first stages of the circuit is sketched by a box only. The protection diode ESD compact models include effects such as voltage overshoot due to forward recovery [15], reverse breakdown, and conductivity modulation due to high injection. Applying a positive HBM stress between the input pin and ground leads to a main current flow through D2 and the protection NPN, which goes into snapback and, therefore, limits the voltage at the VCC line. The voltage at the input pin is given by the sum of the voltages at VCC and the voltage drop across D2. Due to voltage overshoot, the voltage drop across D2 can exceed the stationary DC voltage drop considerably. It is shown that the transient voltage peak at the input pin is reduced by increasing the triggering speed of the protection NPN using an external base resistance. The external base resistance decreases the amount of current needed to forward-bias the base-emitter junction and, therefore, the snapback occurs earlier. If the HBM precharge voltage increases from 2 kV to 4.5 kV, the protection NPN transistor is damaged by the second breakdown. In the circuit simulation shown in Figure 13, this happens as soon as the protection NPN temperature reaches a predefined critical temperature Tc.

«Fig.13.» Increasing the HBM stress voltage to 4.5 kV leads to damage of the protection NPN transistor. This is modeled by an abrupt and irreversible voltage drop at a predefined critical temperature Tc. Time axis is plotted in linear scale.
Summary
ESD is a real threat to IC reliability; therefore, meeting ESD robustness specifications is mandatory. Treating ESD-related problems is a challenging task. The use of TCAD to simulate and investigate ESD-related problems enables robust and reliable design of ESD protection devices/circuits, thereby reducing IC development costs and cycle time.
However, reliable modeling of devices and circuits under ESD stress conditions requires specialized knowledge and broad experience. The TCAD-driven ESD methodology, which has been developed by the Synopsys Consulting and Engineering group and has been outlined in this article, has a proven track record of success in helping customers meet their challenges of treating ESD-related problems. The two service offerings, TCAD ESD Workbench and ESD Compact Model Development, can be customized specifically to protect your IC products from ESD damage.
Contact tcad_team@synopsys.com for more information on our ESD service offerings.
References
[1] “Fundamentals of ESD, Part One–An Introduction to ESD,” Electrostatic Discharge Association. Article available at <http://www.esda.org/basics/part1.cfm>, May 2007.
[2] J. E. Barth et al., “TLP Calibration, Correlation, Standards, and New Techniques,” IEEE Transactions on Electronics PackagingManufacturing, vol. 24, no. 2, pp. 99–108, 2001.
[3] G. Notermans, P. de Jong, and F. Kuper, “Pitfalls when correlating TLP, HBM and MM testing,” in Electrical Overstress/ElectrostaticDischarge Symposium (EOS/ESD), pp. 170–176, 1998.
[4] M. P. J. Mergens, On-Chip ESD Protection in Integrated Circuits: Device Physics, Modeling, Circuit Simulation, Ph.D. thesis, ETHZurich, Switzerland, 2001.
[5] K. Esmark, H. Gossner, and W. Stadler, Advanced Simulation Methods for ESD Protection Development, Amsterdam: Elsevier,2003.
[6] C. Russ et al., “Non-Uniform Triggering of gg-nMOSt Investigated by Combined Emission Microscopy and Transmission Line Pulsing,” in Electrical Overstress/Electrostatic DischargeSymposium (EOS/ESD), pp. 177–186, 1998.
[7] C. H. Díaz, S.-M. Kang, and C. Duvvury, “Simulation of Electrical Overstress Thermal Failures in Integrated Circuits,” IEEETransactions on Electron Devices, vol. 41, no. 3, pp. 359–366, 1994.
[8] C. Salaméro et al., “Accurate prediction of the ESD robustness of semiconductor devices through physical simulation,” in 43rdAnnual International Reliability Physics Symposium, San Jose, CA, USA, pp. 106–111, 2005.
[9] D. Pogany et al., “Quantitative Internal Thermal Energy Mapping of Semiconductor Devices Under Short Current Stress Using Backside Laser Interferometry,” IEEE Transactions on ElectronDevices, vol. 49, no. 11, pp. 2070–2079, 2002.
[10] “Simulation of Current Filament During Electrostatic Discharge Pulse (Z-2007.03),” available from SolvNet <https://solvnet. synopsys.com/retrieve/020415.html>, May 2007.
[11] V. Vassilev et al., “A CAD assisted design and optimisation methodology for over-voltage ESD protection circuits,” in 15thEuropean Symposium on Reliability of Electron Devices, FailurePhysics and Analysis (ESREF), Zurich, Switzerland, 2004.
[12] J. Li, S. Joshi, and E. Rosenbaum, “A Verilog-A Compact Model for ESD Protection NMOSTs,” in Proceedings of the IEEECustom Integrated Circuits Conference, San Jose, CA, USA, pp. 253–256, September 2003.
[13] S. L. Miller, “Ionization Rates for Holes and Electrons in Silicon,” Physical Review, vol. 105, no. 4, pp. 1246–1249, 1957.
[14] H. Wolf, H. Gieser, and W. Wilkening, “Analyzing the
Switching Behavior of ESD - Protection Transistors by Very Fast
Transmission Line Pulsing,” in Electrical Overstress/ElectrostaticDischarge Symposium (EOS/ESD), Orlando, FL, USA, pp. 28–37, September 1999.
[15] K. J. Tseng, “Modelling of diode forward recovery characteristics using a modified charge-control equation,” International Journalof Electronics, vol. 84, no. 5, pp. 437–444, 1998.






