(рамный узел)
Исходные данные: hb =1200 мм; bf = 300 мм; tf = 20 мм; tw = 10 мм;
сварка ручная; RA = 400 кН; сталь С285.
Исходя из предельного момента, который может воспринять балка, запроектировать жесткий узел сопряжения ее с колонной (hk = 500 мм).
Р Е Ш Е Н И Е
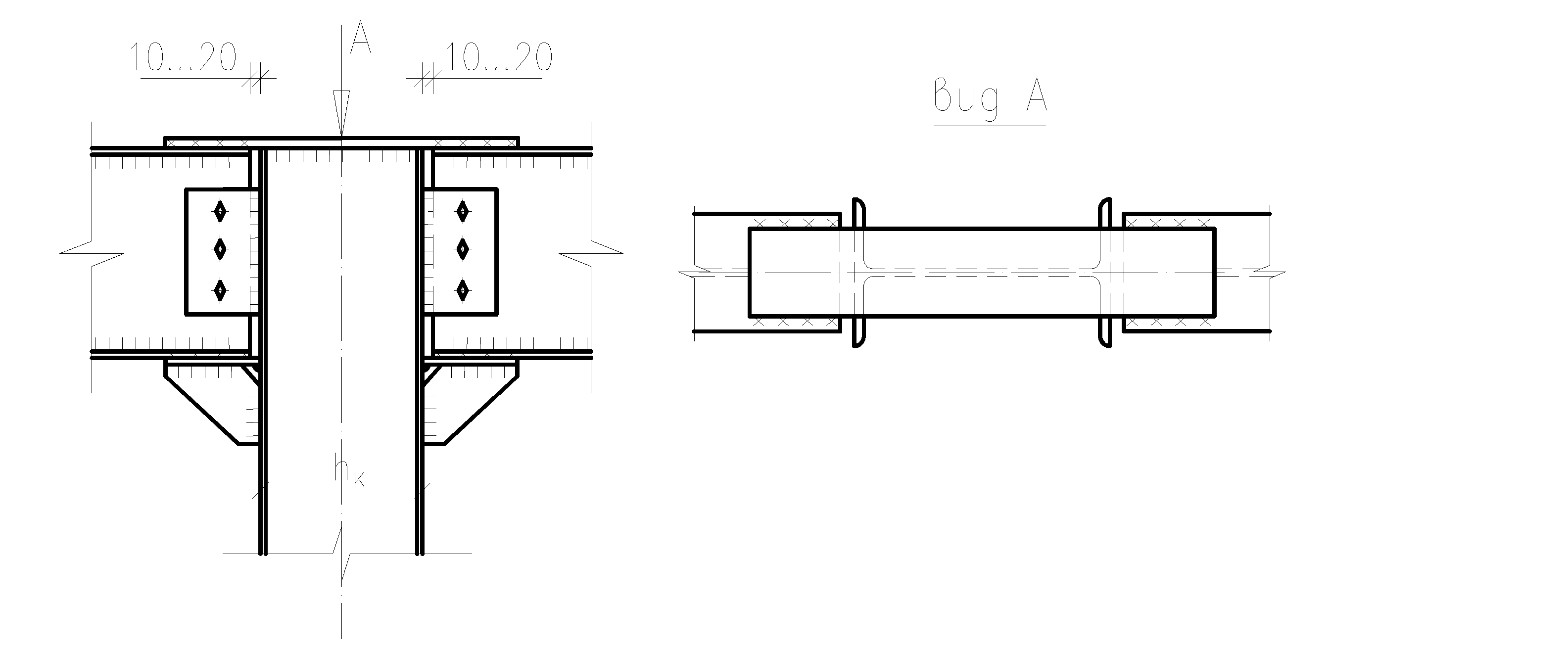
Рис. 19
1. Определим предельный момент Mu.
Jx = Jw + 2 Jf = tw∙ hw 3 / 12 + 2∙ (bf∙ tf 3 / 12 + bf∙ tf∙ h0 2 / 22 ) =
= 1∙ 1163 / 12 + 2∙ [30∙ 23 / 12 + 30∙ 2∙ (118 / 2)2] = 339183 см4;
Wx = 2 Jx / hb = 2∙ 339183 / 120 = 5653 см3;
Mu = Ry∙ γc∙ Wx = 26 ∙ 1,0 ∙ 5653 = 146979 кН ∙ см.
2. Найдем усилие в поясах:
NF = Mu / h0 = 146979 / (120 – 2) = 1246 кН.
3. Определим, по какому сечению шва необходимо вести расчет:
βf∙ Rwf· γwf = 0,7· 20· 1,0 = 14 кН/см2;
βz∙ Rwz∙ γwz = 1,0∙ 0,45∙ 38∙ 0,85 = 14,54 кН/см2.
Расчет необходимо проводить по металлу шва.
4. Установим размеры накладки:
An ≥ Af; Af = 30 ∙ 2 = 60 см2; примем bn∙ tn = 260 ∙ 24 мм; An = 62,4 см2 > Af.
5. Рассчитаем швы, прикрепляющие накладку к верхнему поясу, приняв kf = kmin = 8 мм:
lw ≥ N / (βf· κf· Rwf· γwf· γc) = 1246 / (0,7 ∙ 0,8 ∙ 20 ∙ 1,0 ∙ 1,0) = 111,25 см.
Так как длина швов получилась большой, примем катет kf = 20 мм.
lw ≥ 1246 / (0,7 ∙ 2 ∙ 20 ∙ 1,0 ∙ 1,0) = 44,6 см.
Таким образом, по обе стороны накладки необходимо наложить шов длиной l = lw / 2 + 1 cм = 44,6 / 2 + 1 = 23,3 cм.
Примем l = 24 см, зазор Δ = 20 мм; тогда общая длина накладки
ln = 2∙ (24 +2) + 50 = 102 см.
6. Нижний пояс приваривается к опорному столику. Длина швов с каждой стороны пояса балки также должна быть равна 24 см.
Отсюда выступающая сторона столика (горизонтальный лист) l + Δ =
= 24 + 2 = 26 cм. Толщину столика примем равной толщине пояса балки 20 мм; ширину – bf + 2 a = 30 + 2∙ 2 = 34 см.
7. Рассчитаем сварные швы, прикрепляющие опорный столик, состоящий из горизонтального листа и вертикального ребра, к колонне.

Так как нижний пояс балки приварен к опорному столику, условно примем, что опорная реакция RA передается на столик по центру тяжести швов (учитывая зазор Δ = 20 мм, он находится на расстоянии е = 140 мм от грани колонны). Момент от эксцентричного приложения силы RA воспринимается швами, которыми крепится горизонтальный лист столика и опорное ребро, а поперечная сила – в основном вертикальными швами, приваривающими ребро столика к колонне.
В нашем случае M = RA∙ e = 400 ∙ 14 = 5600 кН∙см и Q = RA = 400 кН.
Примем катет шва kf = 16 мм. На рисунке в) показаны сечения швов, воспринимающие передаваемые усилия M и Q (учтены расчетные длины швов lw = l – 1 см).
Найдем центр тяжести сечения швов относительно оси x 1 – x 1:
ΣSx 1 = 2∙ 0,7∙ 1,6∙ 252 / 2 + 2∙ 0,7∙ 1,6∙ 33∙ (25 + 4 + 1) = 2917,6 см3;
(здесь второй член в уравнении определен приблизительно);
ΣAw = 2∙ 0,7∙ 1,6∙ 25 + 2∙ 0,7∙ 1,6∙ 33 = 129,92 см2;
yct = ΣSx 1 / ΣAw = 2917 / 129,92 ≈ 22,5 см.
Момент инерции швов относительно оси x – x, проходящей через центр тяжести сечения швов:
Jx = 2 [0,7∙ 1,6∙ 252 / 12 + 0,7∙ 1,6∙ 25∙ (22,5 – 25 / 2)2] +
+ [33∙ (2∙ 0,7∙ 1,6)3 / 12 + 2∙ 0,7∙ 1,6∙ 33∙ (25 + 4 + 1 – 22,5)2] = 12705,5 см4;
(здесь также второй член определен приблизительно);
Wx,min = 12705,5 / 22,5 = 564,7 см3.
Проверим прочность швов:
σw = M / Wx,min = 5600 / 564,7 = 9,92 кН/см2;
τw = Q / Aw = 400 / 129,92 = 3,1 кН/см2;
√σw 2 + τw 2 = √ 9,922 + 3,12 = 10,4 кН/см2 < Rwf∙ γwf∙ γc = 18 кН/см2.
Прочность швов обеспечена.
Базы центрально-сжатых колонн
Общие указания
Требуемая площадь плиты базы определяется из условия прочности бетона фундамента при местном сжатии:
Apl,req = N /(Rb,loc·γc),
где N – усилие в нижнем сечении колонны, распределяемое плитой базы;
Rb,loc = α·φ·Rb – расчетное сопротивление бетона при местном сжатии;
Rb – призменная прочность бетона;
α = 1 – для бетонов класса ниже В25;
φ – коэффициент повышения прочности бетона при местном сжатии на площади Apl, < Aфун (Aфун – площадь фундамента по его верхнему обрезу), рекомендуется принимать в пределах 1,2…1,5.
Размеры плиты в плане B, L устанавливаются, исходя из Apl,req и конструктивных ограничений; минимальный размер свеса плиты с, закрепляемого анкерными болтами М24…М30, принимается равным 80…90 мм при шарнирном сопряжении колонн с фундаментом и 20…40 мм – при жестком.
При шарнирном сопряжении колонны с фундаментом анкерные болты ставятся лишь для фиксации проектного положения колонны и закрепления ее в процессе монтажа. Анкеры в этом случае прикрепляются непосредственно к опорной плите базы. Благодаря гибкости плиты обеспечивается податливость сопряжения при действии случайных эксцентриситетов. При жестком сопряжении анкеры прикрепляются к стержню колонны через выносные консоли и затягиваются с напряжением, близким к расчетному сопротивлению, что устраняет возможность поворота колонны.
Толщина плиты определяется из условия ее сопротивления изгибу
tpl,req = √ 6 Mmax / (Ry∙ γc),
где Mmax – наибольший изгибающий момент в плите на различных ее участках от распределенного реактивного давления фундамента σb, зависящий от условий опирания плиты на торец колонны и элементов базы (траверсы, ребра).
Прикрепление траверс и ребер к стержню колонны рассчитывается на усилия, передаваемые с соответствующей грузовой площади плиты;при совместном действии на прикрепление сдвигающих усилий и моментов прочность угловых швов проверяется по результирующим касательным напряжениям, прочность стыковых швов – по приведенным напряжениям.
Прикрепление стержня колонны, траверс, ребер к плите базы угловыми швами проверяется на прочность при условном срезе по металлу шва или по металлу границы сплавления. В базах с фрезерованным торцом такая проверка не нужна.
Прочность траверс и ребер проверяется условным расчетом на поперечный изгиб без учета их совместной работы с плитой базы.
Примеры расчета баз
Центрально сжатых колонн
Пример 1.
Исходные данные: N = 3210кН; сталь С235; стержень – сварной
двутавр: h = 500 мм; вf = 500 мм; tw = 8 мм; tf = 16 мм.
1. Примем для фундамента бетон класса В7.5 (Rb = 0,45 кН/см2) и определим расчетное сопротивление бетона смятию:
Rb,loc = α·φ·Rb = 1∙ 1,2∙ 0,45 = 0,54 кН/см2.
2. Определение размеров опорной плиты в плане.
Конструкцию базы примем с двустенчатыми общими траверсами.
Требуемая площадь опорной плиты
Apl,req = N / Rb,loc = 3210 / 0,54 = 5944 см2.
Назначим толщину траверс ttr = 10 мм, а вылет консольной части с = 80 мм. Тогда ширина плиты
B = bf + 2∙ (ttr + c) = 500 + 2∙ (10 + 80) = 680 мм.
Требуемая длина плиты
Lreq = Apl,req / B = 5944 / 68 = 87,4 см.
Примем размеры плиты L x B = 880 x 680 мм.
3. Определение толщины плиты.
Среднее напряжение в бетоне фундамента
σb = N / (L ∙B) = 3210 / (88 ∙ 68) = 0,536 кН/см2 < 0,54 кН/см2.
Определим изгибающие моменты на участках плиты:
· Участок 1 (плита, опертая на 4 канта) – b = 468 мм; a = 250 мм;
b/a = 468 / 250 = 1,872. По табл. 6.8 [2], интерполируя, получим α 1 = 0,09688.
Тогда M 1 = α 1 ∙ σb∙ a 2 = 0,09688 ∙ 0,536 ∙ 252 = 32,5 кН ∙ см.
· Участок 2 (плита, опертая на 3 канта) – b= 190 мм; a = 500 мм;
b / a = 190 / 500 = 0,38 < 0,5. В этом случае плита рассчитывается с коэффициентом β = 0,125:
M 2 = β∙ σb∙ a 2 = 0,125 ∙ 0,536 ∙ 502 = 167,5 кН∙ см.
Этот момент значительно превышает изгибающий момент на участке 1. Уменьшим размеры участка постановкой ребра посередине участка 2. Тогда b / a = 190 / 250 = 0,76. Интерполируя, по табл. 6.9 [2] получим β = 0,0934.
M 2 = 0,0934 ∙ 0,536 ∙ 2 52 = 31,3 кН∙ см.
· Участок 3 (консольная плита).
M 3 = σb∙ c 2 / 2 = 0,536 ∙ 82 / 2 = 17,15 кН∙ см.
Наибольший момент получен на участке 1, уменьшить размеры которого затруднительно. Определяем толщину плиты, исходя из момента на этом участке:
tpl = √ 6 Mmax / (Ry∙ γc) = √ 6 ∙ 32,5 / (23 ∙ 1,0) = 2,91 см.
Примем tpl = 30 мм.
4. Расчет траверсы.
Принимаем ручную сварку. Тогда для г. Якутска (район I1):
βf∙ Rwf∙∙ γwf = 0,7 ∙ 18 ∙ 0,85 = 10,71 кН/см2;
βz∙ Rwz∙ γwz = 1,0 ∙ 0,45 ∙ 36∙ 0,85 = 13,77 кН/см2.
Определяющим является расчет по металлу шва.
Необходимая высота траверсы при 4-х сварных швах с катетом kf = ttr = = 10 мм, прикрепляющих листы траверсы к полкам колонны, составит
htr = N / [ 4 kf (βf∙ Rwf∙∙ γwf)∙γc] + 1 см =
= 3210 / (4∙ 1,0∙ 0,7∙ 18∙ 0,85∙ 1,0) + 1 = 75 см.
Примем высоту траверсы htr = 750 мм.
Отметим, что такой расчет справедлив при условии передачи усилия N на опорную плиту только через траверсы.
Проверим прочность траверсы на изгиб и срез. На траверсу передается реактивный отпор фундамента с половины площади плиты. Траверса рассчитывается как однопролетная балка с консолями; опоры балки находятся в сечениях, где траверса приваривается к стержню колонны.
Погонная нагрузка на траверсу составит
qtr = σb∙ (bf / 2 + ttr + c) = 0,536 ∙ (50 / 2 + 1 + 8) = 18,2 кН/см.
Изгибающий момент в месте приварки траверсы к колонне
Mtr = qtr∙ ctr 2 / 2 = 18,2 ∙ 192 / 2 = 3285,1 кН∙см.
Поперечная сила в это же сечении
Qtr = qtr∙ ctr = 18,2 ∙ 19 = 345,8 кН.
Момент сопротивления траверсы
Wtr = ttr∙ htr 2 / 6 = 1 ∙ 752 / 6 = 937,5 см3.
Условие прочности по нормальным напряжениям
Mtr / (Wtr∙ Ry∙ γc) = 3285,1 / (937,5 ∙ 23∙ 1,0) = 0,152 << 1.
Условие прочности по касательным напряжениям
Qtr / (htr∙ ttr∙ Rs∙ γc) = 345,8 / (75 ∙ 1,0 ∙ 0,58 ∙ 23 ∙ 1,0) = 0,35 < 1.
5. Расчет ребер усиления плиты (на участке 2).
Ребра рассчитывают как консоли; нагрузка на них собирается с соответствующей грузовой площади. В нашем последняя равна половине площади участка 2.
Погонная нагрузка на ребро
qr = σb∙ bf / 2 = 0,536 ∙ 50 / 2 = 13,4 кН/см.
Изгибающий момент в ребре
Mr = qr∙ br 2 / 2 = 13,4 ∙ 192 / 2 = 2418,7 кН∙см.
Поперечная сила в том же сечении
Qr = qr∙ br = 13,4 ∙ 19 = 254,6 кН.
Требуемая высота ребра, при толщине ее равной толщине траверсы
hr = √ 6 Mr / (tr∙ Ry∙ γc) = √ 6 ∙ 2418,7 / (1 ∙ 23∙ 1,0) = 25,1 см.
Примем высоту ребра hr = 300 мм.
Проверим прочность ребра на срез
Qr / (hr∙ tr∙ Rs∙ γc) = 254,6 / (30 ∙ 1,0 ∙ 0,58 ∙ 23 ∙ 1,0) = 0,636 < 1.
Сварные швы, прикрепляющие ребра к колонне, необходимо проверить на прочность от действия равнодействующей касательных напряжений от изгиба и среза. Примем катет шва kf = ttr = 10 мм.
Проверим прочность на срез по металлу шва
τw = √ { 6 Mr / [βf∙ kf ∙ 2 (hr – 1см ) 2 ]} 2 + {Qr / [βf ∙kf∙∙ 2 (hr – 1 см )]) 2 =
= √ {6∙ 2418,7 / [0,7∙ 1,0∙ 2∙ (30 – 1)2]}2 + (254,6 / [0,7∙ 1,0∙ 2∙ (30 – 1)]}2 =
= 13,83 кН/см2 < 18∙ 0,85 = 15,3 кН/см2 .
Проверим прочность швов на срез по металлу границы сплавления:
τw = √ { 6 Mr / [βz∙ kf ∙ 2 (hr – 1см ) 2 ]} 2 + {Qr / [βz ∙kf∙∙ 2 (hr – 1 см )]) 2 =
= √ {6∙ 2418,7 / [1,0∙ 1,0∙ 2∙ (30 – 1)2]}2 + (254,6 / [1,0∙ 1,0∙ 2∙ (30 – 1)]}2 =
= 9,68 кН/см2 < 0,45∙ 36∙ 0,85 = 13,8 кН/см2 .
6. Расчет швов, прикрепляющих траверсы и ребра к опорной плите.
Требуемый катет швов крепления траверсы к плите:
kf ≥ qtr∙ L / [βf∙∙(L + 2 c)∙ Rwf∙∙ γwf =
= 18,2∙ 88 / [0.7∙ (88 + 2∙ 190∙ 18∙ 0,85] = 1,187 см.
Примем kf = 12 мм.
Требуемый катет швов крепления ребер к плите:
kf ≥ Qr / (βf∙∙ 2 br∙ Rwf∙∙ γwf) =
= 254,6 / (0.7∙ 2∙ 19∙ 18∙ 0,85) = 0,63 см.
Примем kf = 10 мм (одинаковым со швами прикрепления ребер к колонне). Такие же швы примем конструктивно для крепления наружных граней поясов колонны к опорной плите.

Рис. 20
Пример 2.
Исходные данные: стержень – прокатный двутавр №40К2; сталь С235;
N = 3210 кН; Rb,loc = 0,54 кН/см2.
1. Взяв из предыдущего примера Apl,req = 5944 см2, примем В = 600 мм. Тогда требуемая длина опорной плиты Lreq = Apl,req / B = 5944 / 60 = 99,1 см. Примем размеры опорной плиты L x B = 1000 x 600 мм.
2. Среднее напряжение в бетоне фундамента
σb = N / (L ∙B) = 3210 / (100 ∙ 60) = 0,535 кН/см2 < 0,54 кН/см2.
3. Определение толщины плиты.
Изгибающие моменты на участках плиты:
· Участок 1 (плита, опертая на 4 канта) – b = 400 - 2∙ 20 = 360 мм;
a = 200 – 13 / 2 = 193,5 мм;
b/a = 360 / 193,5 = 1,86. По табл. 6.8 [2], интерполируя, получим α 1 = 0,1313.
Тогда M 1 = α 1 ∙ σb∙ a 2 = 0,1313 ∙ 0,535 ∙ 19,352 = 26,3 кН ∙ см.
· Участок 2 (плита, опертая на 4 канта) – b= 400 мм;
a = 1000 / 2 – 200 -10 – 90 = 200 мм;
b / a = 400 / 200 = 2. В этом случае α 2 = 0,132:
M 2 = α 2 ∙ σb∙ a 2 = 0,132 ∙ 0,535 ∙ 202 = 28,25 кН∙ см.
· Участок 3 (плита, опертая на 3 канта).
а = 400 мм; b = 90 мм; b / a = 90 / 400 = 0,225 < 0,5.
Данный участок при этом можно рассматривать как консольную плиту:
M 3 = σb∙ b 2 / 2 = 0,535 ∙ 92 / 2 = 21,67 кН∙ см.
Такой же момент будет на участке 4.
По наибольшему моменту определяем толщину плиты:
tpl = √ 6 Mmax / (Ry∙ γc) = √ 6 ∙ 28,25 / (23 ∙ 1,0) = 2,72 см.
Примем tpl = 28 мм.
4. Расчет траверсы.
Принимаем полуавтоматическую сварку. Тогда
βf∙ Rwf∙∙ γwf = 0,8 ∙ 18 ∙ 0,85 = 12,24 кН/см2;
βz∙ Rwz∙ γwz = 1,0 ∙ 0,45 ∙ 36∙ 0,85 = 13,77 кН/см2.
Определяющим является расчет по металлу шва.
Необходимая высота траверсы при 4-х сварных швах с катетом kf = ttr = = 10 мм, прикрепляющих листы траверсы к полкам колонны, составит
htr = N / [ 4 kf (βf∙ Rwf∙∙ γwf)∙γc] + 1 см =
= 3210 / (4∙ 1,0∙ 0,8∙ 18∙ 0,85∙ 1,0) + 1 = 66,6 см.
Примем высоту траверсы htr = 670 мм.
Проверим прочность траверсы на изгиб и срез.
Погонная нагрузка на траверсу составит
qtr = σb∙ (bf / 2 + ttr + c) = 0,535 ∙ (40 / 2 + 1 + 9) = 16,05 кН/см.
Изгибающий момент в сечениях, где траверса приваривается к колонне
Mtr = qtr∙ ctr 2 / 2 = 16,05 ∙ 302 / 2 = 7222,5 кН∙см.
Поперечная сила в этих же сечениях
Qtr = qtr∙ ctr = 16,05 ∙ 30 = 481,5 кН.
Момент сопротивления траверсы
Wtr = ttr∙ htr 2 / 6 = 1 ∙ 672 / 6 = 748 см3.
Условие прочности по нормальным напряжениям
Mtr / (Wtr∙ Ry∙ γc) = 7222,5 / (748 ∙ 23∙ 1,0) = 0,42 < 1.
Условие прочности по касательным напряжениям
Qtr / (htr∙ ttr∙ Rs∙ γc) = 481,5 / (67 ∙ 1,0 ∙ 0,58 ∙ 23 ∙ 1,0) = 0,54 < 1.
5. Расчет диафрагмы.
В запас прочности диафрагма рассматривается как балка, шарнирно закрепленная по концам (в месте приварки ее к траверсам).
Нагрузка на диафрагму собирается с грузовой площади, равной произведению свеса плиты на участке 3 и половине расстояния между диафрагмой и стержнем колонны на длину диафрагмы Agr = (9 + 20 / 2)∙ 40 = 760 см2.
Погонная нагрузка на диафрагму
qd = σb∙ Agr / ld = 0,535 ∙ 760 / 40 = 10,165 кН/см.
Изгибающий момент в диафрагме
Mr = qd∙ ld 2 / 8 = 10,165 ∙ 402 / 8 = 2033 кН∙см.
Поперечная сила на опоре
Qd = qd∙ ld / 2 = 10,165 ∙ 40 / 2 = 203,3 кН.
Требуемая высота диафрагмы для восприятия изгибающего момента, при толщине ее равной толщине траверсы
hdМ= √ 6 Md / (td∙ Ry∙ γc) = √ 6 ∙ 2033 / (1,0 ∙ 23∙ 1,0) = 7,28 см.
То же, для восприятия поперечной силы
hdQ = Qd / (td∙ Rs∙ γc) = 203,3 / (1,0∙ 0,58∙ 23∙ 1,0) = 15,2 см.
Принимаем высоту диафрагмы hd = 160 мм.
Проверим прочность швов, прикрепляющих диафрагму к траверсам:
τw = Q / (n ∙kf ∙βf∙ lw) = 203,3 / [2∙ 1,0∙ 0,8∙ (16 – 1)] = 8,5 кН/см2 <
< Rwf ∙ γwf∙ γc = 18∙ 0,85∙ 1,0 = 15,3 кН/см2 .
6. Расчет швов, соединяющих траверсы и опорную плиту.
lw = 2 (L – 2 см ) + 4 [(L – hk) – 4 см ] =
= 2∙ (100 – 2) + 4∙ [(100 – 40] – 4) = 420 см.
kf ≥ 2 qtr∙ L / (lw∙ βf ∙ γwf∙ γc) = 2∙ 16,05∙ 100 / (420∙ 0,8∙ 18∙ 0,85∙ 1,0) = 0,62 см.
Примем kf = 7 мм, что согласуется с табл. 38* [1].

Рис. 21
Пример 3.
 Исходные данные: см. пример 1.
Исходные данные: см. пример 1.
Рис. 22
В примере 1 траверса запроектирована достаточно большой высоты. Заметим, что при этом в расчете приняты некоторые допущения, которые идут в запас прочности.
Более точный расчет, учитывающий опирание на плиту и траверсы и торца колонны, приведен ниже, при этом пункты 1…3 примера 1 остаются без изменений.
4. Расчет траверсы.
Грузовая площадь, с которой собирается нагрузка на траверсу, представляет собой сумму площадей участков 1, 2 и 3 (см. рис.):
Agr, 1 = 1/2 (bv 1 + bn 1 )∙ h 1 = 1/2∙ (6,75 + 19)∙ 12,25 = 157,72 см2.
Здесь bv 1 = 190 – 245 / 2 = 67,5 мм.
Agr, 2 = 1/2 (bv 2 + bn 2 )∙ h 2 = 1/2∙ (22,3 + 46,8)∙ 12,25 = 423,24 см2.
Здесь bv 2 = 468 – 2∙ 122,5 = 223 мм.
Agr, 3 = c∙ L = 8∙ 88 = 704 см2.
Agr = Σ Agr,I = 2 Agr, 1 + Agr, 2 + Agr, 3 = 2∙ 157,72 + 423,24 + 704 = 1442,7 см2.
Нагрузка, приходящаяся на траверсу, составит
Ntr = σb∙ Agr = 0,536∙ 1442,7 = 773,3 кН.
При ручной сварке, как это было выявлено в примере 1, определяющим при расчете угловых швов является расчет по металлу шва.
Необходимая длина швов для крепления траверсы к стержню колонны:
lw = Ntr / [ 2 kf (βf∙ Rwf∙∙ γwf)∙γc] = 773,3 / (2∙ 1,0∙ 0,7∙ 18∙ 0,85∙ 1,0) = 36,1 см.
Примем высоту траверсы htr = lw + 1 см = 36,1 + 1 =37, 1 см ≈ 380 мм.
Проверим прочность траверсы на изгиб и срез.
Погонная нагрузка на траверсу:
qtr = Ntr / L = 773,3 / 88 = 8,8 кН/см.
Изгибающий момент в месте приварки траверсы к колонне:
Mtr,op = qtr∙ ctr 2 / 2 = 8,8 ∙ 192 / 2 = 1588,4 кН∙см.
Поперечная сила в этом же сечении (слева):
Qtr,lev = qtr∙ ctr = 8,8 ∙ 19 = 167,2 кН.

Рис. 23
Изгибающий момент в пролетной части траверсы:
Mtr,pr = qtr∙ l 2 / 8 = 8,8 ∙ 502 / 8 = 1161,6 кН∙cм.
Поперечная сила справа:
Qtr,pr = qtr∙ L / 2 - Qtr,lev = 8,8∙ 88 / 2 – 167,2 = 220 кН.
Проверка прочности: Wtr = 1∙ 382 / 6 = 240,7 см3;
σtr = Mtr,op / Wtr = 1588,4 / 240,7 = 6,6 кН/см2 < Ry∙γc = 23 кН/см2;
τtr = Qtr,pr / Atr = 220 / (1 ∙ 38) = 5,8 кН/см2 < Rs∙γc = 13,34 кН/см2;
σef = √σtr 2 + 3 τtr 2 = √ 6,62 + 3∙ 5,82 = 12 кН/см2 < 1,15 Ry∙γc = 26,45 кН/см2.
5. Расчет ребра усиления плиты.
Нагрузка на ребро собирается с удвоенной площади участка 4:
Agr,r = 2 Agr, 4 = 2 Agr, 1 = 2∙ 157,72 = 315,44 см2.
Nr = σb∙ Agr,r = 0,536 ∙ 315,44 = 169,1 кН.
Погонная нагрузка на ребро
qr = Nr / br = 169,1 / 19 = 8,9 кН/см.
Далее расчет аналогичен приведенному в примере 1.
Mr = 8,9∙ 192 / 2 = 1606,2 кН∙см;
Qr = 8,9∙ 19 = 169,1 кН;
hr = √ 6∙ 1606,2 / (1,0∙ 23∙ 1,0) = 20,47 см.
Примем hr = 240 мм.
Условие прочности по касательным напряжениям
169,1 / (24 ∙ 1,0 ∙ 0,58 ∙ 23 ∙ 1,0) = 0,53 < 1.
Прочность швов на срез по металлу границы сплавления:
τw = √ { 6 Mr / [βz∙ kf ∙ 2 (hr – 1см ) 2 ]} 2 + {Qr / [βz ∙kf∙∙ 2 (hr – 1 см )]) 2 =
= √ {6∙ 1606,2 / [0,7∙ 1,0∙ 2∙ (24 – 1)2]}2 + (169,1 / [0,7∙ 1,0∙ 2∙ (24 – 1)]}2 =
= 14 кН/см2 < 15,3 кН/см2 .
Пример 4.
Исходные данные: N = 4500 кН; сталь С345; бетон фундамента В12;
стержень колонны – из 2-х двутавров №40Ш1.
Р Е Ш Е Н И Е
1. Выпишем из [1] необходимые данные для расчета:
Ry = 31,5 кН/cм2; Run = 47 кН/cм2; Rwf = 21,5 кН/cм2;
Rwz = 0,45 Run = 0,45∙ 47 = 21,15 кН/cм2; Rb = 0,75 кН/cм2;
βf = 0,7; βz = 1,0; γwf = 1,0; γwz = 0,85.
2. Определим размеры опорной плиты.
Rb,loc = α·φ·Rb = 1∙ 1,2∙ 0,75 = 0,9 кН/см2.
Apl,req = N / Rb,loc = 4500 / 0,9 = 5000 см2.
B = hk + 2 c = 388 +2∙ 80 = 548 мм.
Примем В = 550 мм. Тогда L= Apl,req / B = 90,9 см. Принимаем L= 910 мм.
Толщину траверсы примем равной ttr = 12 мм. Тогда (см. рис.)
c = B / 2 - hk / 2 – ttr = 550 / 2 – 388 / 2 – 12 = 69 мм;
b = 400 – 9,5 = 390,5 мм; а = 388 мм; а 1 = 388 мм; b 1 = 255 мм.
3. Определим толщину плиты.
Среднее напряжение в бетоне фундамента
σb = N / (L ∙ B) = 4500 / (91 ∙ 55) = 0,899 кН/cм2 < Rb,loc = 0,9 кН/cм2.
· Участок 1. b / a = 390,5 / 388 ≈ 1,0 α 1 = 0,048;
M 1 = α 1 ∙ σb∙ a 2 = 0,048 ∙ 0,899 ∙ 38,82 = 64,96 кН ∙ см.
· Участок 2. b 1 / a 1 = 255 / 388 = 0,6572 β = 0,082;
M 2 = β∙ σb∙ a 12 = 0,082 ∙ 0,899 ∙ 38,82 = 111,0 кН ∙ см.
· Участок 3.
M 3 = σb∙ c 2 / 2 = 0,899 ∙ 6,92 / 2 = 21,4 кН∙ см.
Как видно, моменты на участках очень сильно различаются.
Определим, каким должен быть консольный свес плиты с, чтобы моменты на участках 1 и 3 были одинаковыми.
c = √ 6 M 1 / σb = √ 6 ∙ 54,96 / 0,899 = 12,02 см. Примем с = 120 мм.
Тогда В = 388 + 2∙ 120 = 628 мм. Примем В = 630 мм.
Длина плиты при этом должна быть L = 5000 / 63 = 79,4 см.
Примем L = 800 мм. Новый размер свеса составит с = 315 – 194 – 12 =
= 109 мм. Среднее напряжение в бетоне
σb = 4500 / (80 ∙ 63) = 0,893 кН/cм2
Участок 3.
M 3 = σb∙ c 2 / 2 = 0,893 ∙ 10,92 / 2 = 53 кН∙ см.
Участок 1.
M 1 = α 1 ∙ σb∙ a 2 = 0,048 ∙ 0,896 ∙ 38,82 = 64,5 кН ∙ см.
Моменты на этих участках выравнялись.
Отношение размеров участка 2 стало: b 1 / a 1 = 205 / 388 = 0,5155 β = 0,0622;
M 2 = β∙ σb∙ a 12 = 0,0622 ∙ 0,896 ∙ 38,82 = 83,86 кН ∙ см.
Максимальный момент возникает на участке 2.Толщина плиты при этом
tpl = √ 6 Mmax / (Ry∙ γc) = √ 6 ∙ 83,86 / (31,5 ∙ 1,0) = 3,99 см.
Эта толщина близка к предельно допустимой.
Изменим размеры участка 2 путем постановки ребра, разделяющего его пополам (см. рис.). Тогда размеры участка 2* станут такими:
b 1 = 200 мм; a 1 = 388 / 2 = 194 мм;
b 1 / a 1 = 200 / 194 = 1,031 ≈ 1,03 β = 0,1132;
M 2* = β∙ σb∙ a 12 = 0,1132 ∙ 0,896 ∙ 19,42 = 38,2 кН ∙ см.
В этом случае максимальный момент будет на участке 1, размеры которого изменить затруднительно.
tpl = √ 6 Mmax / (Ry∙ γc) = √ 6 ∙ 64,5 / (31,5 ∙ 1,0) = 3,5 см.
Примем толщину плиты tpl = 36 мм.
4. Определим высоту траверсы.
Выясним, по какому сечению необходимо вести расчет:
βf∙ Rwf· γwf = 0,7· 21,5· 1,0 = 15,05 кН/см2;
βz∙ Rwz∙ γwz = 1,0∙ 21,15∙ 0,85 = 17,98 кН/см2.
Определяющим является расчет по металлу шва.
Примем kf = 14 мм, принимая во внимание то, что tf = 14 мм.
htr = N / [ 4 kf (βf∙ Rwf∙∙ γwf)∙γc] + 1 см =
= 3210 / (4∙ 1,4∙ 0,7∙ 21,5∙ 1,0∙ 1,0) + 1 = 54,4 см.
Примем htr = 550 мм.
5. Определим катет швов, прикрепляющих траверсы к опорной плите (в расчете учтем только длинные швы):
Σlw = 2 L = 2 ∙ 81 = 162 см;
kf ≥ N / (Σlw∙ βf∙∙ Rwf ∙ γwf∙ γc) = 4500 / (162∙ 0,7∙ 21,5∙ 1,0∙ 1,0) = 1,85 см.
Примем kf = 20 мм.
6. Проверим прочность траверсы.
Траверса рассматривается как однопролетная балка с двумя консольными свесами.
Нагрузка на 1 погонный сантиметр листа траверсы
qtr = σb∙ (a 1 / 2 + ttr + c) = 0,896 ∙ (38,8 / 2 + 1,2 + 10,9) = 28,22 кН/см.
Mtr ≈ qtr∙ ltr 2 / 8 = 28,22 ∙ 812 / 8 = 23144 кН∙см.
Момент сопротивления траверсы
Wtr = ttr∙ htr 2 / 6 = 1,2 ∙ 552 / 6 = 605 см3.
Условие прочности по нормальным напряжениям
Mtr / (Wtr∙ Ry∙ γc) = 23144 / (605 ∙ 31,5∙ 1,0) = 1,21 > 1.
Прочность не обеспечена.
Примем tf = 16 мм. Тогда Wtr = 1,6 ∙ 552 / 6 = 807 см3.
Mtr / (Wtr∙ Ry∙ γc) = 23144 / (807 ∙ 31,5∙ 1,0) = 0,91 < 1.
Прочность траверсы обеспечена.
7. Расчет ребра.
Погонная нагрузка на ребро
qr = σb∙ a 1* = 0,896 ∙ 19,42 = 17,38 кН/см.
Изгибающий момент в ребре
Mr = qr∙ b 12 / 2 = 17,38 ∙ 202 / 2 = 3476 кН∙см.
Поперечная сила в том же сечении
Qr = qr∙ b 1 = 17,38 ∙ 20 = 347,6 кН.
Требуемая высота ребра, при толщине ее равной толщине траверсы
hr = √ 6 Mr / (tr∙ Ry∙ γc) = √ 6 ∙ 3476 / (1,6 ∙ 31,5∙ 1,0) = 20,3 см.
Примем высоту ребра hr = 220 мм.
Условие прочности ребра на срез
Qr / (hr∙ tr∙ Rs∙ γc) = 347,6 / (22 ∙ 1,6 ∙ 0,58 ∙ 31,5 ∙ 1,0) = 0,54 < 1.
8. Расчет сварных швов, прикрепляющих ребра к колонне.
Проверяем на прочность от действия равнодействующей касательных напряжений от изгиба и среза. Примем катет шва kf = 1,2 tr = 1,2∙ 16 ≈20 мм.
Проверим прочность на срез по металлу шва
τw = √ {6∙ 3476 / [0,7∙ 2,0∙ 2∙ (22 – 1)2]}2 + (347,6 / [0,7∙ 2,0∙ 2∙ (22 – 1)]}2 =
= 18 кН/см2 < 21,5 кН/см2 .

Рис. 24
Пример 5.
Исходные данные: N = 1580 кН; бетон фундамента – В12 (= 0,75 кН/см2;
колонна двухветвевая из швеллеров №27; сталь – С245.
Р Е Ш Е Н И Е
1. При расчете стержня колонны было принято жесткое сопряжение колонны с фундаментом и определено расстояние между наружными гранями ветвей В = 300 мм.
2. Определим необходимую площадь опорной плиты:
Apl,req = N / (Rb,loc∙γc) = 1580 / (0,9 ∙ 1,0) = 1756 см2,
где Rb,loc = α·φ·Rb = 1∙ 1,2∙ 0,75 = 0,9 кН/см2.
Примем габариты плиты L х B = 420 х 420 мм; Apl = 42∙ 42 = 1764 см2.
 Конструкцию базы примем с двустенчатыми раздельными траверсами (см. рис. 25).
Конструкцию базы примем с двустенчатыми раздельными траверсами (см. рис. 25).
Рис. 25
3. Определим толщину плиты.
Среднее напряжение в бетоне
σb = 1580 / 1764 = 0,896 кН/cм2.
· Участок 1. b / a = 300 / 270 = 1,11 α 1 = 0,055;
M 1 = α 1 ∙ σb∙ a 2 = 0,055 ∙ 0,896 ∙ 272 = 35,9 кН ∙ см.
· Участок 2. b 1 / a 1 = 60 / 270 = 0,22 < 0,5; в этом случае момент определяется как для консоли длиной «b»
M 2 = σb∙ b 2/ 2 =0,896 ∙ 62 = 16,13 кН ∙ см.
· Участок 3. b / a = 65 / 220 = 0,295 < 0,5
M 3 = 0,896 ∙ 6,52 / 2 = 18,93 кН∙ см.
Так как момент на участке 1 намного превышает моменты на других участках, уменьшим его размеры постановкой диафрагмы, приваренной к ветвям колонны (см. рис.).
· Участок 1* (измененный): b / a = 300 / 135 = 2,22 > 2.
В этом случае момент определяется как в однопролетной шарнирно опертой балке - α 1 = 0,125;
M 1 = α 1 ∙ σb∙ a 2 = 0,125 ∙ 0,896 ∙ 13,52 = 20,41 кН ∙ см.
По наибольшему моменту определяем требуемую толщину опорной плиты
 tpl = √ 6 Mmax / (Ry∙γc) = √ 620,41 / (24 ∙ 1,0) = 2,26 см.
tpl = √ 6 Mmax / (Ry∙γc) = √ 620,41 / (24 ∙ 1,0) = 2,26 см.
Принимаем tpl = 24 мм.
4. Расчет траверс.
Элементы траверс привариваются к ветвям колонны восемью сварными швами.
Выявим прочность сварных швов при ручной сварке:
βf∙ Rwf∙∙ γwf = 0,7 ∙ 18 ∙ 0,85 = 10,71 кН/см2;
βz∙ Rwz∙ γwz = 1,0 ∙ 0,45 ∙ 37∙ 0,85 = 14,15 кН/см2.
Расчет необходимо вести по металлу шва.
Приняв kf = tr = 10 мм, получим
htr,req = Ntr / [ 8 kf (βf∙ Rwf∙∙ γwf)∙γc] = 1580 / (8∙ 1,0∙ 0,7∙ 18∙ 0,85∙ 1,0) = 18,44 см
Примем htr = 200 мм.
Проверим прочность траверсы на изгиб и срез. Траверса рассматривается как консольная балка, защемленная в месте ее примыкания к стенке швеллера.
Погонную нагрузку одного листа траверсы в запас прочности (без учета влияния ребер опорных столиков) можно принять
qtr = σb∙ (a / 2 + ttr + c) = 0,896 ∙ (27 / 2 + 1 + 6,5) = 18,8 кН/см.
Изгибающий момент и поперечная сила в траверсе
Mtr = qtr∙ b 2 / 2 = 18,8 ∙ 62 / 2 = 338,4 кН∙см.
Qtr = qtr∙ b = 18,8 ∙ 6 = 112,8 кН.
Момент сопротивления листа траверсы
Wtr = ttr∙ htr 2 / 6 = 1 ∙ 202 / 6 = 66,7 см3.
Условие прочности по нормальным напряжениям
Mtr / (Wtr∙ Ry∙ γc) = 338,4 / (66,7 ∙ 24∙ 1,0) = 0,21 << 1.
Условие прочности по касательным напряжениям
Qtr / (htr∙ ttr∙ Rs∙ γc) = 112,8 / (20 ∙ 1,0 ∙ 0,58 ∙ 24 ∙ 1,0) = 0,405 < 1.
Прочность траверс обеспечена. Большой запас обусловлен тем, что высота траверс определялась, исходя из прочности сварных швов, прикрепляющих их к ветвям.
5. Расчет диафрагмы.
Диафрагма, уменьшающая размеры участка 1, соединяется с ветвями колонны (швеллеры) угловыми сварными швами. Поэтому ее необходимая высота должна определяться прочностью этих швов.
Расчетную схему диафрагмы в запас прочности можно рассматривать как балку на двух опорах, нагруженную распределенной нагрузкой, собранной с соответствующей грузовой площади. Эту грузовую площадь (опять же в запас прочности) можно определить так:
Agr,d = a / 2∙ b = 27 / 2∙ 30 = 405 см2.
Погонная нагрузка на диафрагму составит
qd = σb∙ Agr,d / ld = 0,896∙ 405 / 30 = 12,1 кН/см.
Тогда
Md = 12,1∙ 302 / 8 = 1361 кН∙см;
Qd = 12,1∙ 30 = 181,5 кН.
Требуемый момент сопротивления диафрагмы по условию прочности на изгиб
Wd,req = Md / (Ry∙ γc) = 1361 / (24∙ 1,0) = 56,7 см3.
Тогда требуемая высота диафрагмы
hd,req = √ 6 Wd,req / td = √ 6∙ 1361 / 1,0 = 18,44 см.
Примем hd = 190 мм.
Условие прочности по касательным напряжениям
Qtr / (hd∙ td∙ Rs∙ γc) = 181,5 / (19 ∙ 1,0 ∙ 0,58 ∙ 24 ∙ 1,0) = 0,686 < 1.
5а. Уточненный расчет диафрагмы.
При условии приварки ветвей колонны грузовая площадь диафрагмы составит (см. рис.):
Agr,d = 1/2∙ (bn + bv) ∙ 2 h = 1/2∙ (30 + 16,5)∙ 2∙ 6,75 = 313,86 см2.

Рис. 26
Погонная нагрузка на диафрагму составит
qd = σb∙ Agr,d / ld = 0,896∙ 313,86 / 30 = 9,4 кН/см.
Тогда, рассматривая диафрагму как балку, защемленную по обоим концам, получим
Md = 9,4∙ 302 / 12 = 705 кН∙см;
Qd = 9,4∙ 30 = 141 кН.
Требуемый момент сопротивления диафрагмы по условию прочности на изгиб
Wd,req = Md / (Ry∙ γc) = 705 / (24∙ 1,0) = 29,4 см3.
Требуемая высота диафрагмы
hd,req = √ 6 Wd,req / td = √ 6∙ 29,4 / 1,0 = 13,3 см.
Примем hd = 140 мм.
Условие прочности по касательным напряжениям
Qtr / (hd∙ td∙ Rs∙ γc) = 141 / (14 ∙ 1,0 ∙ 0,58 ∙ 24 ∙ 1,0) = 0,724 < 1.

Рис. 27
6. Расчет швов, прикрепляющих диафрагму к колонне, на равнодействующую касательных напряжений от изгиба и среза.
Проверим прочность на срез по металлу шва
τw = √ { 6 Mr / [βf∙ kf ∙ 2 (hd – 1см ) 2 ]} 2 + {Qr / [βf ∙kf∙∙ 2 (hd – 1 см )]) 2 =
= √ {6∙ 705 / [0,7∙ 1,0∙ 2∙ (14 – 1)2]}2 + (254,6 / [0,7∙ 1,0∙ 2∙ (14 – 1)]}2 =
= 19,5 кН/см2 > 15,3 кН/см2.
Прочность швов не обеспечена. Увеличим высоту диафрагмы hd = 160 мм.
Проверим прочность на срез по металлу шва
τw = √ {6∙ 2418,7 / [0,7∙ 1,0∙ 2∙ (16 – 1)2]}2 + (254,6 / [0,7∙ 1,0∙ 2∙ (16 – 1)]}2 =
= 15,02 кН/см2 < 18∙ 0,85 = 15,3 кН/см2 .
Проверим прочность швов на срез по металлу границы сплавления:
τw = √ { 6 Mr / [βz∙ kf ∙ 2 (hr – 1см ) 2 ]} 2 + {Qr / [βz ∙kf∙∙ 2 (hr – 1 см )]) 2 =
= √ {6∙ 2418,7 / [1,0∙ 1,0∙ 2∙ (16 – 1)2]}2 + (254,6 / [1,0∙ 1,0∙ 2∙ (16 – 1)]}2 =
= 10,51 кН/см2 < 0,45∙ 37∙ 0,85 = 14,15 кН/см2 .
7. Расчет швов, прикрепляющих траверсы и диафрагму к опорной плите.
Требуемый катет швов крепления траверсы к плите:
kf ≥ qtr∙ Ltr / [βf∙∙(Ltr + b)∙ Rwf∙∙ γwf =
= 18,8∙ (2∙ 2 + 2∙ 1 + 6) / [0.7∙ (2∙ 2 + 2∙ 1 + 6 + 6)∙ 18∙ 0,85] = 1,17 см.
Примем kf = 12 мм.
Требуемый катет швов крепления диафрагмы к плите:
kf ≥ qd∙ Ld / (βf∙∙ 2 Ld∙ Rwf∙∙ γwf) =
= 9,4∙ 30 / (0.7∙ 2∙ 30∙ 18∙ 0,85) = 0,45 см.
По таблице 38* [1] при толщине плиты tpl = 24 мм минимальный размер катета шва kf = 8 мм.
Пример 6. База с фрезерованным торцом.
 Исходные данные те же, что и в примере 5, но:
Исходные данные те же, что и в примере 5, но:
Стержень колонны из двутавра №26К3 (h = 262 мм; bf = 260 мм).
Приближенный расчет
1. При фрезерованном торце стержня колонны плиту обычно принимают квадратной. Габаритные размеры опорной плиты определяются аналогично примеру 5.
2. Плита работает как пластинка на упругом основании, воспринимающее давление, сконцентрированное на участке, ограниченном контуРис. 28 ром стержня колонны.
Ведя расчет в запас прочности, можно определить изгибающий момент в плите по кромке колонны, рассматривая трапецеидальный участок плиты как консольную балку с поперечным сечением b∙ tpl, где b – ширина плиты у кромки стержня колонны.
Изгибающий момент в месте сопряжения плиты с колонной равен
M = σb∙ A∙c,
где А – площадь трапеции, заштрихованной на рисунке;
с – расстояние от центра тяжести трапеции до кромки колонны.
Площадь трапеции равна
A = 1/2 (bn + bv)∙ h = 1/2 (42 + 26,2)∙ (21 – 13) = 272,8 см2.
Размер с составит
c = ( 2 bn + bv) h / [ 3 ∙ (bn + bv)] = (2 ∙ 42 +26,2) ∙ 8 / [3∙ (42 + 26,2)] = 4,3 см.
Тогда
М = 0,896∙ 272,8∙ 4,3 = 1053,2 кН∙ см.
Требуемая толщина плиты
tpl = √ 6 M / b∙ Ry = √ 6 ∙ 1053,2 / (26,2∙ 24) = 3,17 см.
Принимаем tpl = 32 мм.
Уточненный расчет
Точный расчет, учитывающий фактический пространственный изгиб плиты, для прямоугольной пластинки весьма сложен, однако он может быть упрощен, если заменить прямоугольную плиту и сечение колонны равновеликими им по площади кругами.
1. Площадь контура колонны: Ak = h∙ bf = 26,2∙ 26 = 681,2 см2.
2. Диаметр эквивалентного по площади круга: Ak* = π∙ d 2 / 4;
dk = √ 4 Ak / π = √ 4 ∙ 681,2 / 3,14 = 29,5 см.
3. Площадь плиты Apl = 42 x 42 = 1764 см2; отсюда
dpl = √ 4 ∙ 1764 / 3,14 = 47,4 см.
4. Отношение «радиуса колонны» к «радиусу плиты»
β = dk / dpl = 0,62 ≈ 0,6.
Тогда коэффициенты, зависящие от отношения «радиуса колонны» к «радиусу плиты» kr = 0,02и kτ = 0,0377 (по табл. 6.10 [2]);
5.Вычислим изгибающие моменты в радиальном Mr и тангенциальном Mτ направлениях при ширине расчетного элемента 1 см:
Mr = kr∙ N = 0,02 ∙ 1580 = 31,6 кН∙ см;
Mτ = kτ∙ N = 0,0377 ∙ 1580 = 59,6 кН∙ см;
6. По найденным моментам определяем нормальные и касательные напряжения, приняв толщину плиты tpl = 36 мм (больше, чем в упрощенном расчете):
σr = 6 Mr / tpl 2 = 6∙ 31,6 / 3,62 = 14,63 кН/см2;
στ = 6 Mτ / tpl 2 = 6∙ 59,6 / 3,62 = 27,59 кН/см2;
τ = N / ( 2 π∙ b∙ tpl) = 1580 / (2 ∙ 3,14 ∙ 26,2 ∙ 3,6) = 2,67 кН/см2.
7. Прочность проверяется по приведенным напряжениям по формуле
σуf = √ σr 2 + στ 2 – σr∙ στ + 3 τ 2 =
√ 14,632 + 27,592 – 14,63∙ 27,59 + 3∙ 2,672 = 24,35 кН/см2 <
< 1,15 Ry ∙ γc = 1,15∙ 24∙ 1,0 = 27,6 кН/см2.
Прочность обеспечена.
Пример 7. Исходные данные: колонна из двутавра №26К1;
N = 1580 кН; бетон фундамента – В12 (Rb = 0,75 кН/cм2);
 сталь С245 (Ry = 24 кН/см2).
сталь С245 (Ry = 24 кН/см2).
Рис. 29
Примем конструктивное решение базы с ребрами (см. рис.).
Ребра разделяют опорную плиту на два участка: 1-ый – плита, опертая на три канта и 2-ой – консольная плита.
Проверим возможность приварки ребра к стенке стержня колонны. В соответствии с рис. 4.21,б [2] при размерах с = 131 мм < 400 мм и а = 210 мм сварка возможна, если 2 с ≥ а. В нашем случае 2 с = 2∙ 131 = 262 мм > 210 мм, то есть приварка возможна.
1. Определим толщину опорной плиты.
Участок 1. b / a = 210 / 131 = 1,6 → β = 0,128;
M 1 = β∙ σb∙ a 2 = 0,128∙ 0,896∙ 13,12 = 19,68 кН∙см.
Участок 2. M 2 = σb∙ c 2 / 2 = 0,896 ∙ 7,92 / 2 = 27,96 кН∙см.
Момент на участке 2 значительно превышает момент на участке 1.
С целью выравнивания изгибающих моментов на участках пересмотрим габаритные размеры плиты, принимая во внимание то, что возможности приварки ребра к колонне позволяют это сделать.
Примем размеры плиты 440 х 400 мм. Тогда Apl = 44∙ 40 = 1760 см2 и σb* = = N / Apl = 1580 / 1760 = 0,898 кН/cм2 < σb,loc = 0,9 кН/см2.
Участок 1*. b / a = 220 / 131 = 1,68 → β = 0,1288;
M 1 = β∙ σb∙ a 2 = 0,1288∙ 0,898∙ 13,12 = 19,85 кН∙см.
Участок 2*. M 2 = σb∙ c 2 / 2 = 0,898 ∙ 6,92 / 2 = 21,38 кН∙см.
Требуемая толщина опорной плиты
tpl = √ 6 Mmax / (Ry∙ γc) = √ 6 ∙ 21,38 / (24 ∙ 1,0) = 2,31 см.
Примем tpl = 24 мм.
2. Расчет швов, прикрепляющих ребра к колонне.
А) Ребро, приваренное к стенке колонны.
Погонная нагрузка на ребро составит
qr, 1 = σb∙ a = 0,898 ∙ 13,1 = 11,76 кН/см.
Изгибающий момент и поперечная сила в сечении у места приварки:
Mr, 1 = qr, 1∙ b 2 / 2 = 11,76∙ 222 / 2 = 2845,92 кН∙см;
Qr, 1 = qr, 1∙ b = 11,76∙ 22 = 258,72 кН.
Определим требуемую высоту ребра из условия восприятия им изгибающего момента, приняв толщину ребра tr = 10 мм:
Wr 1, req = Mr, 1 / (Ry∙ γc) = 2845,92 / (24∙ 1,0) = 118,58 см3;
hr 1, req = √ 6 ∙ Wr 1, req / tr = √ 6 ∙ 118,58 / 1,0 = 26,67 см.
Учитывая, что кроме изгибающего момента ребро воспринимает также поперечную силу, примем высоту ребра hr 1 = 310 мм.
Проверим прочность сварных швов на срез, приняв катет шва kf = 10 мм:
- по металлу шва
τw = √ { 6 Mr, 1 / [βf∙ κf∙ 2 ∙(hr 1 – 1 см ) 2 } 2 +
+ { Qr, 1 / [ βf∙∙κf∙ 2 ∙∙(hr 1 – 1 см )} 2 =
= √ {6∙ 2845,92 / [0,7∙ 1,0∙ 2∙ (31 – 1)2}2 + {258,72 / [0,7∙ 1,0∙ (31 - 1)}2 =
= 14,88 кН/cм2 < Rwf∙ γwf∙ γc = 18 ∙ 0,85 ∙ 1,0 = 15,3 кН/cм2;
- по металлу границы сплавления
τw = √ { 6 Mr, 1 / [βя∙ κf∙ 2 ∙(hr 1 – 1 см ) 2 } 2 +
+ { Qr, 1 / [ βя∙∙κf∙ 2 &#






