Й семестр, зачет
ПРОГРАММА ЗАЧЕТА
I. Эллипс, гипербола, парабола
1. Эллипс и его свойства.
2. Гипербола и ее свойства.
3. Парабола и ее свойства.
4. Директориальные свойства эллипса, гиперболы.
5. Полярные уравнения эллипса, гиперболы, параболы.
II. Общая теория линий второго порядка
6. Линия второго порядка (ЛВП).
7. Векторы и прямые асимптотического направления относительно линии 2-го порядка, тип линии. Асимптотические направления. Вектор асимптотического направления для линии параболического типа
8. Центр ЛВП. Центральные и нецентральные линии.
9. Касательная к ЛВП. Обыкновенные и особые точки. Уравнение касательной к ЛВП.
10. Диаметр ЛВП, свойства, сопряженные диаметры.
11. Сопряженные направления относительно ЛВП.
12. Главные направления относительно ЛВП
13. Главные диаметры ЛВП, свойства.
III. Поверхности второго порядка в евклидовом пространстве
14. Поверхности вращения.
15. Эллипсоид и его свойства.
16. Однополостный гиперболоид и его свойства.
17. Двуполостный гиперболоид и его свойства
18. Эллиптический параболоид и его свойства.
19. Гиперболический параболоид и его свойства.
20. Прямолинейные образующие поверхностей второго порядка.
21. Цилиндрические поверхности и их уравнения. Цилиндрические поверхности второго порядка.
22. Конические поверхности и их уравнения. Коническая поверхность второго порядка.
IV. Преобразования плоскости
23. Отображения и преобразование множеств. Примеры. Группа преобразований множества и ее подгруппы.
24. Движения плоскости. Свойства движений плоскости. Примеры. Основная теорема о движении плоскости. Аналитическое задание движения плоскости. Примеры движений 1 и 2 рода.
25. Представление движений в виде композиции осевых симметрий.
26. Группа движений плоскости и ее подгруппы
27. Группа симметрий геометрической фигуры
28. Гомотетия плоскости и ее свойства. Аналитическое задание.
29. Подобия плоскости. Свойства. Примеры. Аналитическое задание. Представление подобия в виде композиции гомотетии и движения.
30. Группа подобий плоскости и ее подгруппы.
31. Аффинные преобразования плоскости. Свойства. Примеры. Основная теорема об аффинных преобразованиях. Аналитическое задание аффинных преобразований плоскости.
32. Перспективно-аффинные преобразования плоскости и их свойства. Сдвиг, косое сжатие и их свойства.
33. Группа аффинных преобразований плоскости и ее подгруппы.
34. Приложение преобразований к решению задач элементарной геометрии.
ТРЕБОВАНИЯ К ЗАЧЕТУ
Теоретическая часть: знание определений, уравнений, формулировок теорем по программе курса.
Практическая часть: умение решать задачи по всем разделам курса; иметь отчетность по всем самостоятельным и контрольным работам, которые проводились в течение семестра.
ПОДРОБНО:
- эллипс (Э), гипербола (Г), парабола (П)
Знать: определения; канонические уравнения; все объекты, связанные с Э, Г, П (эксцентриситет, директрисы, асимптоты гиперболы, фокусы, большая и малая полуось, фокальное расстояние, фокальный радиус точки).
Уметь: находить канонические уравнения по различным данным, вычислять эксцентриситет, находить уравнения директрис; находить полярные уравнения по каноническим (канонические уравнения по полярным).
- общая теория линий второго порядка (ЛВП)
Знать определения: ЛВП; асимптотического направления, асимптоты, центра, особой и обыкновенной точек, касательной, диаметра, сопряженных диаметров, сопряженных направлений, главных направлений, главного диаметра.
Знать канонические уравнения ЛВП.
Уметь: определять тип ЛВП, вид ЛВП, асимптотическое направление, центр, сопряженные направления, главные направления; находить уравнения асимптот, касательной, диаметра, главного диаметра; строить сопряженные диаметры; общий диаметр двух ЛВП.
- поверхности второго порядка в евклидовом пространстве
Знать определения: эллипсоида, однополостного гиперболоида, двуполостного гиперболоида, эллиптического параболоида, гиперболического параболоида, поверхности вращения, цилиндрической поверхности, конической поверхности, прямолинейных образующих поверхности.
Знать канонические уравнения всех поверхностей второго порядка.
Уметь: изображать поверхности второго порядка, по каноническому уравнению определять тип поверхности; составлять канонические уравнения по известным сечениям; находить уравнения прямолинейных образующих.
- преобразования плоскости
Знать определения: отображения множеств, инъективного (сюръективного) отображения, биективного отображения, преобразования множества; группы преобразований и ее подгруппы; движения плоскости; тождественного преобразования, параллельного переноса, поворота (в частности, центральной симметрии), осевой симметрии, скользящей симметрии; инвариантной точки (прямой, фигуры); гомотетии, подобия, аффинного преобразования, перспективно аффинного преобразования, косого сжатия, сдвига.
Знать формулировки теорем: основных теорем о движении и об аффинных преобразованиях (с доказательством!!!), об аналитическом задании движений (аффинных преобразований), о свойствах движений (подобий, гомотетии, аффинных преобразований, перспективно аффинных преобразований), об инвариантных точках и прямых движений; о представлении движения композицией не более чем трех осевых симметрий; о разложении подобия в композицию гомотетии и движения.
Уметь: иллюстрировать определения преобразований, строить образы (прообразы) точек при заданном на чертеже преобразовании; указывать инвариантные точки (прямые) преобразований; по формулам определять вид преобразования, находить элементы, задающие это преобразование; составлять формулы преобразования по известным элементам; находить инвариантные точки (прямые) преобразования; находить образы (прообразы) фигур; приводить примеры подгрупп группы преобразований.
ТИПОВЫЕ ЗАДАЧИ
I. Эллипс. Гипербола. Парабола.
1. По уравнению эллипса 4 x 2 + 9 y 2 – 36 = 0 определить: а) его полуоси; б) эксцентриситет; в) уравнения директрис; г) расстояние между фокусами; д) расстояние от вершины до ближайшей директрисы.
2. Дано уравнение гиперболы 25 x 2 – 4 y 2 –100 = 0. Определить а) ее полуоси; б) уравнения асимптот; в) эксцентриситет; г) расстояние между его фокусами; д) уравнения директрис; е) расстояние от вершины до ближайшей директрисы
3. Определить координаты фокуса и уравнение директрисы параболы, если ее уравнение имеет вид:
а) y 2 – 10 x = 0; б) 2 у 2– 3 х = 0; в) 5 x 2 + 4 y = 0.
4. Составить каноническое уравнение гиперболы, если расстояние между ее директрисами равно  , а ее эксцентриситет равен
, а ее эксцентриситет равен  .
.
5. Составить каноническое уравнение параболы, если ее директриса имеет уравнение x +15=0.
6. Найти полярное уравнение кривой, заданной своим каноническим уравнением:
а)  ; б)
; б)  ; в) y2=10x.
; в) y2=10x.
7. Написать каноническое уравнение кривой, заданной своим полярным уравнением:
а)  ; б)
; б) 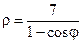 ; в)
; в)