Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,
.
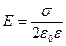Напряженность поля, создаваемого двумя бесконечными равномерно заряженной плоскостями (с поверхностными плотностями зарядов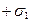 
и 
)
.
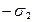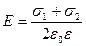При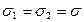 
и разноименных зарядах на плоскостях
.
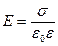Связь потенциала с напряженностью:
а)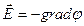 
,
б)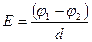 
, в случае однородного поля (в частности поля между обкладками плоского конденсатора);
в)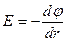 
, в случае поля, обладающего центральной или осевой симметрией.
Электрический момент диполя
,
где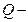 
заряд, 
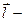плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Работа сил электрического поля по перемещению заряда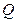 
из точки поля с потенциалом 
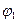в точку поля с потенциалом 
.
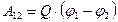Электроемкость
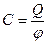, или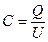 
,
где 
потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю);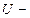 
разность потенциалов пластин конденсатора.
Электроемкость плоского конденсатора
,
где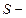 
площадь пластины (одной) конденсатора; 
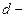расстояние между пластинами.
Электроемкость шара радиусом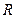 
Электроемкость батареи конденсаторов:
а)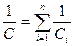 
при последовательном соединении;
б) 
при параллельном соединении,
где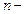 
число конденсаторов в батарее.
Энергия заряженного конденсатора:
, 
.
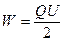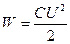
4. Постоянный ток
Основные формулы
Сила постоянного тока
,
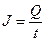где 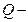заряд, прошедший через поперечное сечение проводника за время 
.
Плотность тока
,
где 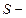площадь поперечного сечения проводника.
Связь плотности тока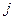 
со средней скоростью 
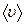направленного движения заряженных частиц
,
где 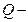заряд частицы; 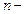концентрация заряженных частиц.
Закон Ома:
а)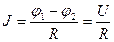 
, – для участка цепи, не содержащего ЭДС, где 
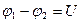, – разность потенциалов (напряжение) на концах участка цепи; 
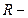сопротивление участка;
б)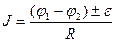 
,– для участка цепи, содержащего ЭДС, где 
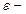ЭДС источника; 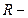полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в)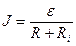 
,– для замкнутой (полной) цепи, где 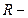внешнее сопротивление цепи; 
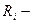внутреннее сопротивление источника тока.
Законы Кирхгофа:
а)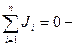 
первый закон;
б)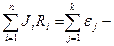 
второй закон,
где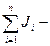 
алгебраическая сумма сил токов, сходящихся в узле; 
алгебраическая сумма произведений сил токов на сопротивления участков;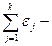 
алгебраическая сумма ЭДС.
Сопротивление 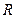и проводимость 
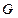проводника
, 
,
где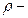 
удельное сопротивление; 
удельная сопротивление;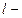 
длина проводника; 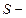площадь поперечного сечения проводника.
Сопротивление системы проводников:
а)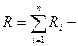 
при последовательном соединении;
б)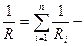 
при параллельном соединении, где 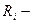сопротивление 
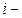того проводника.
Работа тока
.
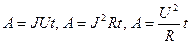Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение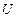 
, последние две – для участка не содержащего ЭДС.
Мощность тока:
.
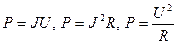Закон Джоуля–Ленца
.
Закон Ома в дифференциальной форме
,
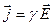
где удельная проводимость;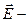 
напряженность электрического поля; 
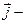плотность тока.
5. Электромагнетизм
Основные формулы
Связь магнитной индукции 
с напряженность магнитного поля
.
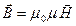где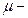 
магнитная проницаемость изотропной среды; 
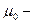магнитная постоянная. Для вакуума 
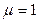, и тогда индукция магнитного поля
.
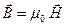Закон Био-Савара-Лапласа
или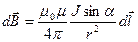 
,
где 
индукция магнитного поля, создаваемого элементом проводника длиной 
с током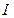 
; 
радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;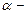 
угол между радиус-вектором и направлением тока в элементе проводника.
Магнитная индукция в центре кругового тока (N витков)
,
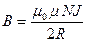где 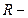радиус кругового витка.
Магнитная индукция на оси кругового тока (N витков)
,
где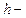 
расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого бесконечного проводника с током
,
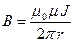где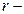 
кратчайшее расстояние от провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком прямого провода с током
,
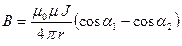где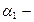 
угол между радиус-вектором, проведенным из начала проводника в определяемую точку и направлением тока в проводнике; 
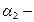угол между радиус-вектором, проведенным из конца проводника в точку и продолжением проводника.
Магнитная индукция поля соленоида бесконечной,, длины, (т.е. когда длина соленоида во много раз больше его диаметра), на его оси
,
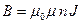где 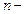число витков соленоида на единице длины соленоида.
Сила, действующая на проводник с током в магнитном поле (закон Ампера)
, или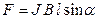 
,
где 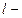длина провода; 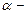угол между направлением тока в проводе и вектором магнитной индукции . Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять лишь к каждому элементу провода в отдельности:
.
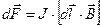Магнитный момент плоского контура с током
,
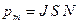где 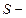площадь контура; 
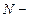число витков в контуре.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,
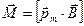или 
,
где 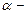угол между векторами 
и .
Потенциальная энергия (т.е. часть полной потенциальной энергии, которая обусловлена существованием вращательного момента) контура с током в магнитном поле
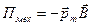или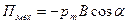 
Отношение магнитного момента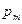 
к механическому 
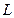(моменту импульса) заряженной частицы, движущейся по круговой орбите,
,
где 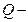заряд частицы; 
масса частицы.
Сила Лоренца
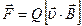, или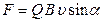 
,
где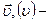 
скорость частицы, 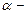угол между векторам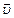и 
и .
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
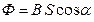или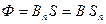 
,
где 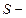площадь контура; 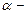угол между нормалью к плоскости контура и вектором магнитной индукции; 
– проекция вектора магнитной индукции на нормаль к поверхности,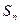 
– проекции поверхности 
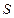на направление перпендикулярное вектору .
б) в случае неоднородного поля и произвольной поверхности
,
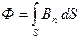где интегрирование ведется по всей поверхности .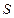
Потокосцепление (полный поток)
.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу витков.
Работа по перемещению замкнутого контура в магнитном поле
.
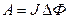ЭДС индукции
.
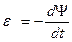Разность потенциалов на концах проводника, движущегося со скоростью в магнитном поле,
,
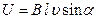где 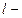длина проводника; 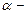угол между векторам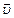и и .
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего контур,
,
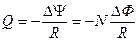где 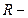сопротивление контура.
Индуктивность контура (с одним витком)
Индуктивность катушки (с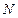 
витками)
.
Индуктивность соленоида
,
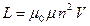где 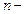число витков на единицу длины соленоида; 
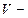объем соленоида.
Мгновенное значение силы тока в цепи, содержащей сопротивление 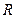и индуктивность :
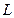а)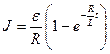 
(при замыкании цепи), где 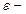ЭДС источника тока; t– время, прошедшее после замыкания цепи;
б) 
(при размыкании цепи), где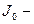 
сила тока в цепи в момент времени 
; 
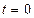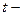время, прошедшее с момента размыкания цепи.
Энергия магнитного поля, создаваемого током в проводнике, контуре, соленоиде
.
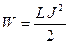Объемная плотность энергии магнитного поля (отношение энергии магнитного поля к его объему)
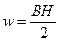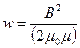или 
и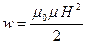 
,
где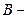 
магнитная индукция; 
напряженность магнитного поля.
Оптика
Основные формулы
Скорость света в среде
,
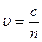где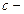 
скорость света в вакууме; 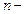абсолютный показатель преломления среды.
Оптическая длина пути световой волны
,
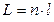где 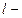геометрическая длина пути световой волны в среде с показателем преломления 
.
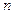Оптическая разность хода двух световых волн
.
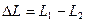Связь разности фаз с оптической разностью хода световых волн
,
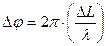где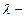 
длина световой волны.
Условие максимального усиления света при интерференции
.
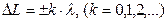Условие максимального ослабления света
.
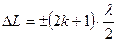Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой плоскопараллельной пленки (пластинки)
,
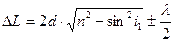или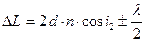 
,
где 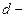толщина пленки; 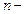абсолютный показатель преломления пленки (пластинки); 
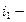угол падения светового луча; 
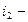угол преломления светового луча в пленке (пластинке).
Радиусы светлых колец Ньютона в отраженном свете
, 
,
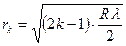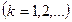где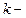 
номер кольца; 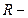радиус кривизны линзы.
Радиусы темных колец Ньютона в отраженном свете
, .
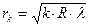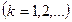Угол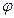 
отклонения световых лучей, соответствующий максимуму (светлая полоса) при дифракции света на одной щели, определяется из условия
,
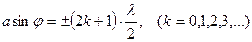где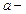 
ширина щели; 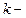порядковый номер максимума.
Угол 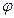отклонения световых лучей, соответствующий максимуму (светлая полоса) при дифракции света на дифракционной решетке (пропускающей), определяется из условия
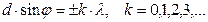
где 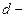период дифракционной решетки; 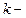порядковый номер максимума.
Разрешающая способность дифракционной решетки
,
где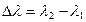 
наименьшая разность дин волн двух соседних спектральных линий (
), при которой эти линии могут быть раздельно видны в спектре, полученном посредством данной решетки; 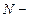полное число щелей решетки.
Формула Вульфа–Брэггов
,
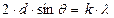где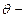 
угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); 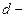расстояние между атомными плоскостями кристалла.
Закон Брюстера
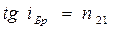
где 
угол падения, при котором отразившийся от плоскости диэлектрика световой луч полностью поляризован; 
относительный показатель преломления второй среды относительно первой.
Закон Малюса
,
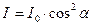где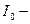 
интенсивность плоскополяризованного света, падающего на поляризатор; 
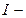интенсивность этого света, после анализатора; 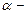угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания вектора напряженности падающего света совпадают с этой плоскостью, то анализатор пропускает данный сет без уменьшения его интенсивности).
Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
а) 
(в твердых телах),
где 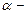постоянная вращения; 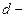длина пути, пройденного светом в оптически активном веществе;
б)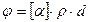 
(в растворах),
где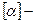 
удельное вращение; 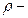массовая концентрация оптически активного вещества в растворе.
Релятивистская масса
,
где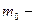 
масса покоя частицы; 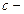скорость света в вакууме; 
скорость частицы.
Взаимосвязь массы и энергии релятивистской частицы
,
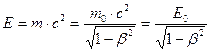где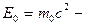 
энергия покоя частицы.
Полная энергия свободной частицы
,
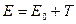где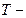 
кинетическая энергия релятивистской частицы.
Кинетическая энергия релятивисткой частицы
, или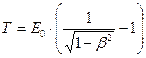 
.
Импульс релятивистской частицы
.
Связь между полной энергией и импульсом релятивисткой частицы
.
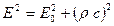Закон Стефана-Больцмана
,
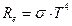где 
энергетическая светимость (излучательность)- абсолютно твердого тела;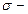 
постоянная Стефана-Больцмана; 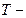термодинамическая температура Кельвина.
Первый закон Вина (закон смещения)
,
где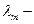 
длина волны, на которую приходится максимум энергии излучения; 
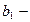первая постоянная Вина.
Второй закон Вина
,
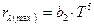где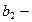 
вторая постоянная Вина; 
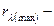максимальная плотность энергетической светимости.
Энергия фотона
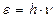или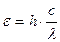 
,
где 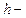постоянная Планка; 
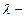частота фотона; длина волны фотона; 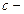скорость света
Масса фотона
.
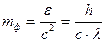Импульс фотона
.
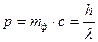Формула Эйнштейна для фотоэффекта
,
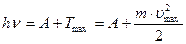где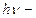 
энергия фотона, падающего на поверхность металла; 
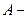работа выхода электрона из металла; 
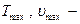максимальная кинетическая энергия и максимальная скорость фотоэлектрона, масса фотоэлектрона.
Красная граница фотоэффекта
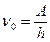, или 
,
где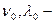 
минимальная частота и максимальная длина волны света, при которой еще возможен фотоэффект; 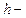постоянная Планка; 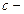скорость света в вакууме.
Давление света при нормальном падении на поверхность
,
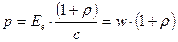где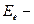 
энергетическая освещенность (облученность); 
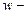объемная плотность энергии излучения; 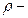коэффициент отражения материала поверхности.
