УЧЕБНЫЕ МАТЕРИАЛЫ ПО РАЗДЕЛАМ КУРСА ФИЗИКИ
Механика
Основные формулы
Движение материальной точки (центра масс твердого тела) вдоль оси  .
.
Средняя (путевая) скорость:
 ,
,
где  путь, пройденный точкой за интервал времени
путь, пройденный точкой за интервал времени  . Путь
. Путь  в отличие от разности координат
в отличие от разности координат  не может убывать и принимать отрицательные значения, т.е.
не может убывать и принимать отрицательные значения, т.е.  .
.
Проекция мгновенной скорости на ось  :
:


Проекция среднего ускорения на ось  :
:

Проекция мгновенного (линейного) ускорения на ось  :
:
 .
.
Формула скорости равнопеременного поступательного движения:
 ,
,
где  начальная скорость (в момент времени
начальная скорость (в момент времени  ); для равнозамедленного движения
); для равнозамедленного движения  , для равноускоренного
, для равноускоренного  ).
).
Формула пути равнопеременного движения:
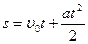 ,
,  .
.
При движении тела по вертикальному направлению в поле силы тяжести Земли  .
.
Движение материальной точки по окружности.
Модуль угловой скорости:
 .
.
Модуль углового ускорения:
 .
.
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
 ,
,  ,
,  ,
,
где  модуль линейной скорости;
модуль линейной скорости;  и
и 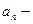 модули тангенциального и нормального ускорений;
модули тангенциального и нормального ускорений;  модуль угловой скорости;
модуль угловой скорости;  модуль углового ускорения;
модуль углового ускорения; 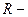 радиус окружности.
радиус окружности.
Модуль полного ускорения:
 .
.
Для равнопеременного вращательного движения  ,
,  ускоренное вращение,
ускоренное вращение,  замедленное вращение.
замедленное вращение.
Угловая скорость
 .
.
Угловое перемещение радиус-вектора (угловой путь):
 ,
,  .
.
Кинематическое уравнение гармонических колебаний материальной точки:  ,
,
где  смещение;
смещение; 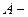 амплитуда колебаний;
амплитуда колебаний;  угловая или циклическая частота;
угловая или циклическая частота;  начальная фаза колебаний.
начальная фаза колебаний.
Скорость и ускорение материальной точки, совершающей гармонические колебания:
 ;
; 
Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания
 ;
;
б) начальная фаза результирующего колебания
 .
.
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях, описываемых уравнениями:
 ,
, 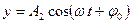 ;
;
а)  , если разность фаз
, если разность фаз  ;
;
б)  , если разность фаз
, если разность фаз  ;
;
в)  , если разность фаз
, если разность фаз  .
.
Уравнение плоской бегущей волны:
 ,
,
где  смещение любой из точек среды с координатой
смещение любой из точек среды с координатой  в момент времени
в момент времени  ;
;  скорость распространения колебаний (волны) в среде.
скорость распространения колебаний (волны) в среде.
Связь разности фаз  колебаний с расстоянием
колебаний с расстоянием  между точками среды, отсчитанных в направлении распространения колебаний:
между точками среды, отсчитанных в направлении распространения колебаний:
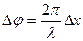 ,
,
где  длина волны.
длина волны.
Импульс абсолютно твердого тела массой  , движущегося со скоростью
, движущегося со скоростью  :
:
 .
.
Второй закон динамики (Ньютона):
 ,
,
где  результирующая сила, действующая на материальную точку.
результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости  ;
;
где  коэффициент упругости (в случае пружины – жесткость);
коэффициент упругости (в случае пружины – жесткость);  абсолютная деформация;
абсолютная деформация;
б) сила тяжести:  ;
;
в) сила трения (скольжения):  ,
,
где  коэффициент трения;
коэффициент трения;  сила нормального давления.
сила нормального давления.
Закон сохранения импульса:
 .
.
Для двух тел для абсолютно упругого удара:
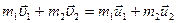 ,
,
где  и
и  - скорости тел перед соударением тел,
- скорости тел перед соударением тел,  и
и  скорости тел в момент после соударения.
скорости тел в момент после соударения.
Для абсолютно неупругого удара двух тел:
 .
.
Кинетическая энергия  тела, движущегося поступательно:
тела, движущегося поступательно:
 , или
, или  .
.
Потенциальная энергия  :
:
а) упругодеформированной пружины:
 ,
,
где  жесткость пружины;
жесткость пружины;  абсолютная деформация;
абсолютная деформация;
б) тела, находящегося в однородном поле силы тяжести:
 ,
,
где  ускорение свободного падения;
ускорение свободного падения;  высота тела над уровнем, принятым за нулевой (формула справедлива при условии
высота тела над уровнем, принятым за нулевой (формула справедлива при условии  , где
, где 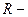 радиус Земли).
радиус Земли).
Закон сохранения механической энергии:
 .
.
Закон сохранения энергии при абсолютно упругом столкновении двух тел, движущихся в горизонтальной плоскости:
 .
.
Закон сохранения энергии при абсолютно неупругом столкновении двух тел, движущихся в горизонтальной плоскости:
 ,
,
где  энергия нагревания тел и их остаточной деформации.
энергия нагревания тел и их остаточной деформации.
Скорости двух тел после абсолютно упругого столкновения:
 ,
,
 .
.
Работа, совершаемая результирующей силой, определяется как мера изменения кинетической энергии:
 .
.
Основное уравнение динамики вращательного движения относительно неподвижной оси:
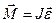 ,
,
где  результирующий вектор моментов внешних сил, действующих на тело, относительно оси вращения;
результирующий вектор моментов внешних сил, действующих на тело, относительно оси вращения;  вектор углового ускорения;
вектор углового ускорения;  момент инерции системы относительно оси.
момент инерции системы относительно оси.
Моменты инерции некоторых тел массой  относительно оси вращения, проходящей через центр масс:
относительно оси вращения, проходящей через центр масс:
а) материальной точки:  ,
,
где  расстояние от материальной точки до оси (модуль радиуса-вектора);
расстояние от материальной точки до оси (модуль радиуса-вектора);
б) стержня длиной  относительно оси перпендикулярной стержню и проходящей через центр масс этого стержня:
относительно оси перпендикулярной стержню и проходящей через центр масс этого стержня:
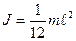 ;
;
в) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра):
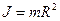 .
.
г) однородного (сплошного) диска (цилиндра) радиусом  относительно оси, перпендикулярной плоскости диска:
относительно оси, перпендикулярной плоскости диска:
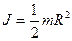 ;
;
д) пустотелого цилиндра с радиусами  и
и  с осью вращения совпадающей с осью цилиндра:
с осью вращения совпадающей с осью цилиндра:
 ;
;
е) шара с осью вращения, проходящей через его центр:
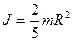 .
.
Теорема Штейнера:
 ,
,
где  момент инерции системы (тела) массой
момент инерции системы (тела) массой  относительно оси проходящей через центр масс системы (тела);
относительно оси проходящей через центр масс системы (тела);  момент инерции системы (тела) относительно оси, не проходящей через центр масс, но параллельной ей,
момент инерции системы (тела) относительно оси, не проходящей через центр масс, но параллельной ей, 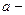 расстояние между осями.
расстояние между осями.
Момент импульса материальной точки массой  , имеющей скорость
, имеющей скорость  и находящуюся на расстоянии
и находящуюся на расстоянии  от оси вращения:
от оси вращения:
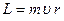 .
.
Момент импульса  тела, вращающегося относительно неподвижной оси
тела, вращающегося относительно неподвижной оси  с угловой скоростью
с угловой скоростью  :
:
 .
.
Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси  :
:

 .
.
Кинетическая энергия тела вращающегося вокруг неподвижной оси:
 , или
, или  .
.
Кинетическая энергия катящегося тела:
 .
.
Молекулярная физика. Термодинамика
Основные формулы
Количество вещества тела (системы), т.е. число структурных элементов (молекул, атомов, ионов и т.д.) содержащихся в теле или системе (выражается в молях):
 ,
,
где  число структурных элементов, составляющих систему;
число структурных элементов, составляющих систему;  постоянная Авогадро (
постоянная Авогадро ( моль-1).
моль-1).
Молярная масса вещества:  ,
,
где  масса однородного тела (системы);
масса однородного тела (системы);  количество вещества этого тела.
количество вещества этого тела.
Количество вещества смеси газов:
 ,
,
или
 ,
,
где  соответственно – количество вещества, число молекул, масса, молярная масса
соответственно – количество вещества, число молекул, масса, молярная масса  того компонента смеси.
того компонента смеси.
Уравнение Менделеева - Клапейрона (уравнение состояния идеального газа):
 ,
,
где  масса газа,
масса газа,  молярная масса газа,
молярная масса газа, 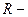 молярная газовая постоянная (
молярная газовая постоянная ( Дж/моль К),
Дж/моль К),  количество вещества (число молей),
количество вещества (число молей),  термодинамическая температура.
термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:
а) закон Бойля- Мариотта (изотермический процесс:  ):
):
 , или для двух состояний газа
, или для двух состояний газа  ;
;
б) закон Гей-Люссака (изобарный процесс:  ):
):
 , или для двух состояний
, или для двух состояний  ;
;
в) закон Шарля (изохорный процесс:  ):
):
 , или для двух состояний
, или для двух состояний  ;
;
г) объединенный газовый закон ( ):
):
 , или
, или  ,
,
где  давление, объем и температура газа в начальном состоянии;
давление, объем и температура газа в начальном состоянии;  те же величины в конечном состоянии.
те же величины в конечном состоянии.
Закон Дальтона, определяющий давления смеси газов:
 ,
,
где  парциальные давления компонентов смеси;
парциальные давления компонентов смеси;  число компонентов смеси.
число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы он только один находился в сосуде, занятом смесью.
Молярная масса смеси газов:
M=  ,
,
где  масса
масса  того компонента смеси;
того компонента смеси;  количество вещества
количество вещества  того компонента смеси;
того компонента смеси;  число компонентов смеси.
число компонентов смеси.
Массовая доля  того компонента смеси газа (в долях единицы или процентах):
того компонента смеси газа (в долях единицы или процентах):
 ,
,
где  масса смеси.
масса смеси.
Концентрация молекул:
 ,
,
где  число молекул вещества, содержащихся в системе;
число молекул вещества, содержащихся в системе;  плотность вещества;
плотность вещества;  объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
Основное уравнение кинетической теории газов:
 ,
,
где  средняя кинетическая энергия поступательного движения молекулы.
средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия поступательного движения молекулы:
 ,
,
где  постоянная Больцмана.
постоянная Больцмана.
Средняя полная кинетическая энергия молекулы:
 ,
,
где  число степеней свободы молекулы.
число степеней свободы молекулы.
Зависимость давления от концентрации молекул и температуры:
 .
.
Скорости молекул:
 средняя квадратичная;
средняя квадратичная;
 средняя арифметическая;
средняя арифметическая;
 наиболее вероятная,
наиболее вероятная,
где 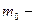 масса одной молекулы.
масса одной молекулы.
Удельные теплоемкости газа при постоянном объеме  и постоянном давлении
и постоянном давлении  , имеющего
, имеющего  степеней свободы:
степеней свободы:

 ,
,  .
.
Связь между удельной и молярной теплоемкостями:
 .
.
Уравнение Майера:  .
.
Внутренняя энергия идеального газа:
 .
.
Первое начало термодинамики:
 ,
,
где  теплота, сообщенная системе (газу);
теплота, сообщенная системе (газу);  изменение внутренней энергии системы;
изменение внутренней энергии системы; 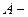 работа, совершенная системой против внешних сил.
работа, совершенная системой против внешних сил.
Работа расширения газа:
 в общем случае;
в общем случае;
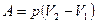 при изобарном процессе;
при изобарном процессе;
 при изотермическом процессе;
при изотермическом процессе;
 при адиабатном процессе, где
при адиабатном процессе, где  показатель адиабаты.
показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
 .
.
Термический КПД цикла:
 ,
,
где  теплота, полученная рабочим телом от теплоотдатчика;
теплота, полученная рабочим телом от теплоотдатчика;  теплота, переданная рабочим телом теплоприемнику.
теплота, переданная рабочим телом теплоприемнику.
Термический КПД цикла Карно

 ,
,
где  и
и  термодинамические температуры теплоотдатчика и теплоприемника.
термодинамические температуры теплоотдатчика и теплоприемника.
Электростатика.
Основные формулы
Закон Кулона
 ,
,
где  сила взаимодействия точечных зарядов
сила взаимодействия точечных зарядов  и
и  ;
; 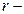 расстояние между зарядами;
расстояние между зарядами; 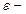 диэлектрическая проницаемость;
диэлектрическая проницаемость;  электрическая постоянная.
электрическая постоянная.
Напряженность электрического поля и потенциал
 ,
,  ,
,
где  потенциальная энергия точечного положительного заряда
потенциальная энергия точечного положительного заряда 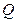 , находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда
 ,
,  .
.
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей),
 ,
,  ,
,
где  напряженность и потенциал поля, создаваемого
напряженность и потенциал поля, создаваемого 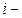 тым зарядом.
тым зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом,
 ,
,  ,
,
где  расстояние от заряда
расстояние от заряда 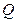 до точки, в которой определяются напряженность и потенциал.
до точки, в которой определяются напряженность и потенциал.
Напряженность и потенциал поля, создаваемого проводящей сферой радиусом 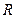 на расстоянии
на расстоянии  от центра сферы:
от центра сферы:
а)  (при
(при 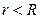 );
);
б)  (при
(при  );
);
в)  (при
(при  ),
),
где 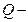 заряд сферы.
заряд сферы.
Линейная плотность заряда
 .
.
Поверхностная плотность заряда
 .
.






