(вместо послесловия)
Управление бизнесом в рыночной экономике характеризуется многими особенностями; выделим некоторые из них. Во-первых, в общей совокупности ресурсов предприятия доминирующее значение приобретают финансовые ресурсы. Во-вторых, принятие управленческих решений финансового характера всегда осуществляется в условиях неопределенности. В-третьих, следствием реальной самостоятельности предприятий становится постоянная забота руководителей по-поводу войска источников финансирования и оптимизации инвестиционной политики. В-четвертых, устанавливая коммерческие отношения с каким-либо контрагентом, можно полагаться исключительно на собственную оценку его финансовой состоятельности.
В этих условиях обоснованность принимаемых управленческих решений, а многие из них, по сути, имеют финансовую природу, в значительной степени определяется качеством финансово-аналитических расчетов. О необходимости систематизации финансовых вычислений и повсеместном их внедрении через систему образования еще в дореволюционной России говорили многие теоретики бухгалтерского учета и финансов. Программа курса "Высшие финансовые вычисления", разработанная проф. Н.С. Лунским, очень высоко оценивалась современниками. Методики анализа баланса, предложенные А.П. Руданов-ским и Н.А. Благовым, до настоящего времени не утратили своей актуальности.
По мере строительства планового социалистического хозяйства в СССР анализ баланса и финансовые вычисления сравнительно быстро были трансформированы в анализ хозяйственной деятельности - направление, "теоретически" обосновывавшее методики управления предприятием в условиях централизованного планирования; что касается блока финансовых дисциплин в целом, то его значимость была существенно принижена. Достаточно упомянуть о том, что курс финансовых вычислений был
выхолощен и низведен с университетского уровня до уровня техникумов - вероятно считалось, что среднего специального образования достаточно для того, чтобы заниматься финансовыми операциями в СССР.
К сожалению, до сих пор еще встречаются рецидивы подобного подхода, проявляющиеся, прежде всего, в высказываниях либо некоторых "чистых" математиков, не нашедших своего места в собственной классической науке и пытающихся "прислониться" к прикладным экономическим разработкам путем бездумной их математизации, когда в угоду красоте математических выкладок выхолащивается экономическая природа изучаемого явления, либо отдельных специалистов, работающих в смежных с бухгалтерско-финансовым блоком дисциплинах (автоматизированные системы управления, математическое моделирование экономических процессов и т.п.). Выдвигаемый ими в качестве аргумента тезис как "заезженная пластинка" повторяет уже не раз слышанное: "в финансовых и коммерческих вычислениях пользуются простым инструментарием, доступным даже школьнику, а потому в университетах следует читать не финансовые вычисления, а финансовую математику".
Здесь возникают, по крайней мере, два вопроса: во-первых, об экономической обоснованности применения тех или иных математических методов и, во-вторых, о допустимой сложности математического аппарата.
Что касается первого вопроса, то в качестве примера, по крайней мере, не вполне оправданного применения математики в экономике можно привести известный в анализе хозяйственной деятельности интегральный метод факторного анализа. Его разработчики, безжалостно критикуя простой и наглядный метод цепных подстановок, говорят о том, что интегральный метод "обеспечивает более высокую точность". Не вдаваясь в комментарий относительно точности в рамках ретроспективного анализа, отмечу только, что обоснованность применения интегрального метода в экономике является исключительно условной, поскольку он требует непрерывности функции, описывающей факторную связь, и бесконечно малого изменения признаков, чего в экономических явлениях часто не может быть в принципе, поскольку многие показатели изменяются дискретно.
По второму вопросу хочется, прежде всего, напомнить, что любые самые сложные вычислительные операции сводятся к четырем элементарным арифметическим действиям. Кроме того, с позиции бухгалтеров и финансистов не абстрактная финансовая математика, а именно финансовые вычисления представляют практический интерес. Финансовые стохастические модели безусловно можно, а для некоторых узких специалистов и следует рассматривать в спецкурсах, что же касается базового математико-аналитического аппарата, к которому, с очевидностью, относятся методы, обсуждаемые в курсе финансовых вычислений, то им должен владеть любой экономист высшей квалификации.
Как мне представляется, научность и значимость любой университетской дисциплины в области прикладной экономики отнюдь не определяются одной лишь сложностью используемого в ней математического инструментария, а пробелы в базовом экономическом образовании, да и в математическом тоже, нигде не проявляются так явно, как в необоснованной математизации процесса принятия управленческого решения. Именно поэтому хочется подчеркнуть, что, обосновывая базовые методы финансовой аналитики, во главу угла нужно ставить экономическую* финансовую природу операции; что касается используемого математического аппарата, то он имеет лишь вспомогательное значение.
Несмотря на кажущуюся простоту расчетов методы финансовых вычислений исключительно важны именно в практической плоскости, и кроме того, они не приходят к специалисту автоматически вместе с дипломом о высшем или специальном образовании. Невозможно стать финансовым менеджером, лишь читая общетеоретические монографии, учебники и руководства,- нужна рутинная вычислительная практика, умение ориентироваться в методах, привлекаемых для получения ряда оценок, которые можно использовать как формализованное обоснование принимаемого решения в области кредитования и финансирования. Именно этому и посвящено данное пособие - решая задачи, можно, образно говоря, "набить руку" на исчислении подобных оценок.
Следует особо подчеркнуть, что изложение аналитического аппарата финансовых операций ни в коем случае нельзя отдавать на откуп "чистым" математикам. Сложность и обоснованность решений финансового характера определяются вовсе не сложностью привлекаемого аппарата; приоритет здесь имеет другое измерение - ответственность за возможные последствия. Так, непродуманно составленный договор о некоторой финансовой операции (ставка, частота и схема начисления, поправка на инфляцию и т.п.) может привести к существенным финансовым потерям независимо от того.Уакой сложности модель была использована, например, для прогнозирования денежного потока. Какими методами обосновано рАшение - это уже другой вопрос; ясно только одно: обоснование < помощью хитроумной математической модели далеко не всегАа минимизирует негативные последствия. Предлагаемое пособий как раз и учит тому, как избежать подобных ошибок.
Повышение правовой, бухгалтерской и финансово-аналитической подготовки экономистов - одно из важнейших направ-, лений совершенствования системы высшего экономического образования. Хочется надеяться, нто со временем в нашей стране культура обоснования и оформления решений финансового характера повысится, а любой грамотный бизнесмен будет понимать, что, например в договоре, содержащем упоминание о процентных платежах, следует указь&ать не номинальную, а эффективную ставку. Печальный опыт российских финансовых пирамид, в частности, говорит и о том, что введение полноценного курса "Финансовые (и коммерческие) вычисления" в университетские программы в духе дореволюционной российской традиции представляется не только оправданным, но и жизненно необходимым.
В. Ковалев
ПРИЛОЖЕ1
Приложение 1
СВОДКА ОСНОВНЫХ ФОРМУЛ
Часто используемые в формулах обозначения; r (d) - годовая
процентная (учетная) ставка (в десятичных дробях); r(m) (d 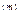 )-номинальная годовая процентная (учетная) ставка (в десятичных дробях, индекс m указывает, сколько раз в течение года происходит наращение или дисконтирование); n, i - продолжительность финансовой операции в годах; t - продолжительность финансовой операции в днях; Т - количество дней в году,,Р - первоначальный капитал; F -наращенный капитал; F
)-номинальная годовая процентная (учетная) ставка (в десятичных дробях, индекс m указывает, сколько раз в течение года происходит наращение или дисконтирование); n, i - продолжительность финансовой операции в годах; t - продолжительность финансовой операции в днях; Т - количество дней в году,,Р - первоначальный капитал; F -наращенный капитал; F 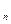 - наращенный капитал за n лет.
- наращенный капитал за n лет.
Процентная ставка: r  =
= 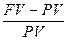 (1)
(1)
гдеPV - предоставляемая в долг сумма,
FV - возвращаемая сумма.
• Учетная ставка:  (2)
(2)
• Соотношение между ставками: rt =  или
или  (3)
(3)
• Дисконт-фактор: v  =
=  (4)
(4)
• Индекс роста капитала: В  =
= 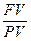 (5)
(5)
• Формула вычисления процентов "со 100 ": 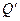 =Qr (6)
=Qr (6)
• Формула вычисления процентов "на 100": S'= 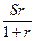 (7)
(7)
• Формула вычисления процентов "во 100": К' = 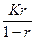 (8)
(8)
• Формула наращения простым» процентами: F = Р(1 + nr). (9)
• Формула простых процентов в случае нецелого числа лет:
F=P(1+  ) (10)
) (10)
Возможны три варианта начисления:
а) точный процент и точная продолжительность периода
(T= 365 или 366 дней, t- точное);
б) обыкновенный процент и точная продолжительность периода
(Т = 360,t- точное);
в) обыкновенный процщтн приблизительная продолжительность периода
(T =360, t - приблизнтельное, когда считается, что в месяце 30 дней).
Дивизор  (11)
(11)
• Формулы для вычисления процентного платежа (при использовании простой ставки):
а) если известна величина капитала (Р): I=Plr; (12)
б) если известна величина капитала, увеличенного на процентный платеж (P+I):
 или
или  (13)
(13)
в) если известна величина капитала, уменьшенного на процентный платеж (Р-I):
 или
или  (14)
(14)
• Формула наращения простыми процентами по переменной процентной ставке:
 (15)
(15)
где на период nк установлена процентная ставка i  и таких периоде m.
и таких периоде m.
• Формула определения простой процентной ставки, доставляющей при наращении такой же результат, как и несколько простых процентных ставок:
 (16)
(16)
где на период n  установлена процентная ставка i
установлена процентная ставка i  и таких периодов m.
и таких периодов m.
• Формула определения величины начисленных процентов за пользование кредитом с учетом уменьшения долга с течением времени:
 (17)
(17)
где к - число погасительных платежей в год, n — срок кредита.
• формула приведенной стоимости (при использовании простой ставки):
 (18)
(18)
• Формула дисконтирования по простой учетной ставке:
P=F(l-nd). (19)
• Формула наращения по простой учетной ставке: F =  . (20)
. (20)
• Формулы для определения срока ссуды (при использовании простой ставки):
n=  или t =
или t =  (21)
(21)
 или
или  (22)
(22)
• Формулы для определения простой ставки:
 или
или 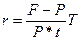 (23)
(23)
 или
или  (24)
(24)
Эквивалентность простых ставок:
 (25)
(25)
 (26)
(26)
• Эквивалентностьпростых ставок при разных временных базах:
 (27)
(27)
 (28)
(28)
где Tr, T 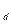 -временные базы, равные количеству дней в году при использовании
-временные базы, равные количеству дней в году при использовании
соответственно процентной и учетной ставок.
Формулы для определения средних значений: а) простой процентной ставки:
 (29)
(29)
 (30)
(30)
б) срока:
 (31)
(31)
 (32)
(32)
где i  ,i
,i  .....im - простые процентные ставки, под которые вмты соответственно суммы P
.....im - простые процентные ставки, под которые вмты соответственно суммы P  ,P
,P  ,:.,Pm на сроки
,:.,Pm на сроки 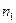 ,n2...,nm.
,n2...,nm.
• Формулы для определения средних значений: а) простой учетной ставки:
 (33)
(33)
 (34)
(34)
б) срока:
 (35)
(35)
 (36)
(36)
где d  ,d2,...,dm - простые учетные ставки, по которым соответственно суммы F
,d2,...,dm - простые учетные ставки, по которым соответственно суммы F  ,F
,F  ,...,Fm учитываются за сроки n
,...,Fm учитываются за сроки n  ,n
,n  ……nm.
……nm.
• Формула наращения простыми процентами с учетом уплаты налога:
 (37)
(37)
где q - ставка налога на проценты.
• Формула наращения по простой учетной ставке с учетом уплаты налога:
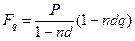 (38)
(38)
где q - ставка налога на проценты.
• Индекс цен (индекс инфляции):
 (39)
(39)
где Р  , P
, P  - стоимости потребительской корзины в начале и в конце периода длительностью t
- стоимости потребительской корзины в начале и в конце периода длительностью t
Темп инфляции:
 (40)
(40)
где Р  , Р2 - стоимости потребительской корзины в начале и в конце периода длительностью t
, Р2 - стоимости потребительской корзины в начале и в конце периода длительностью t
Соотношение между индексом инфляции и темпом инфляции:
 (41)
(41)
• Формула определения индекса инфляции за период при известных индексах инфляции за составляющие его подпериоды:
 (42)
(42)
где I  (h
(h  )-индекс инфляции (темп инфляции) за подпериод ti. подпе-риоды расположены последовательно друг за другом и t=t
)-индекс инфляции (темп инфляции) за подпериод ti. подпе-риоды расположены последовательно друг за другом и t=t  +t
+t  ….t
….t 
• Формула наращения простыми процентами с учетом инфляция:
 (43)
(43)
где 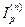 - индекс инфляции за период n.
- индекс инфляции за период n.
• Формулы определения простой, годовой процентной стажки, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной ставке r:
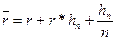 (44)
(44)
 (45)
(45)
где h 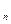 - темп инфляции за период n,
- темп инфляции за период n,
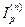 - индекс инфляции за период п.
- индекс инфляции за период п.
Формула определения реальной годовой процентной ставки при. объявленной номинальной процентной ставке в условиях инфляции:
 (46)
(46)
• Формула определения простой годовой учетной ставки, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной ставке d:
 (47)
(47)
• Формула определения реальной годовой учетной ставки при объ-яьпенной номинальной учетной ставке ь условиях инфляции:
 (48)
(48)
• Формула для вычисления величины нового платежа при использовании простой процентной ставки:
 если n
если n  =n
=n  (49)
(49)
где Р  и
и 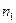 - первоначальный платеж и срок его выплаты, Mq - срок нового
- первоначальный платеж и срок его выплаты, Mq - срок нового
платежа.
• Формула для вычисления срока нового платежа при использовании простой процентной ставки:
 если
если 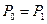 (50)
(50)
где P  и n
и n  - первоначальный платеж и срок его выплаты; Р
- первоначальный платеж и срок его выплаты; Р  - величина нового платежа.
- величина нового платежа.
• Формула определения срока консолидированного платежи при использовании простои процентной ставки:
 (51)
(51)
где платежи P1,P  ..,Pm, уплачиваемыесоотвегстмнно-через ерем n
..,Pm, уплачиваемыесоотвегстмнно-через ерем n  ,n
,n  …..nm, замншотся одним платежом P
…..nm, замншотся одним платежом P  .
.
• Формула для вычисления величины нового платежа при использовании простой учетной ставки:
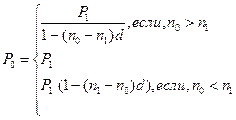 если n
если n  =n
=n  (52)
(52)
где P  и n
и n  - первоначальный платеж и срок его выплаты;
- первоначальный платеж и срок его выплаты;
n  - срок нового платежа.
- срок нового платежа.
• Формула для вычисления срока нового платежа при использовании простой учетной ставки:
 если P
если P  =P
=P  (53)
(53)
где Р  и n
и n  - первоначальный платеж и срок его выплаты; P
- первоначальный платеж и срок его выплаты; P  - величина нового платежа.
- величина нового платежа.
• Формула определения срока консолидированного платежа при использовании простои учетной ставки:
 (54)
(54)
где платежи P  ,P
,P  ...,Pm, уплачиваемые соответственно через время
...,Pm, уплачиваемые соответственно через время
n  ,n
,n  ,...,nm, заменяются одним платежом P
,...,nm, заменяются одним платежом P 
 .
.
• Формула наращения сложными процентами:
 (55)
(55)
где n - число периодов начисления сложных процентов.
• Формула наращения сложными процентами по переменной процентной ставке:
 (56)
(56)
где n  . - количество периодов начисления сложных процентов по процентной
. - количество периодов начисления сложных процентов по процентной
ставке i  , n -общийсрок наращения.
, n -общийсрок наращения.
Формула наращения по смешанной схеме:
 (57)
(57)
где w - целое число периодов начисления сложных процентов, f-дробная часть периода, n=w + f,
• Формула наращения сложными процентами при начислении процентов несколько раз в год:
 (58)
(58)
где n -число лет, m —количество начислений в год.
Формула наращения по смешанной схеме при начислении процентов несколько раз в год:
 (59)
(59)
где n - число лет,
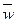 - целое число периодов начисления сложных процентов в n годах,
- целое число периодов начисления сложных процентов в n годах,
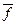 - дробная часть периода, n =
- дробная часть периода, n = 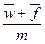 .
.
• Формула для определения срока ссуды (при использовании сложной процентной ставки):
 (60)
(60)
• Формулы для определения номинальной годовой процентной ставки:
 (61)
(61)
 (62)
(62)
где ref - эффективная годовая процентная ставка.
• Формулы определения эффективной годовой процентной ставки:
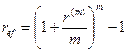
 (63)
(63)
 (64)
(64)
• Формула приведенной стоимости (при использовании сложной ставки):
 (65)
(65)
• Формула приведенной стоимости (при m -кратном начислении процентов в год):
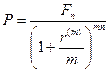 (66)
(66)
• Формула дисконтирования по сложной учетной ставке:
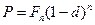 (67)
(67)
где n - число периодов дисконтирования.
• Формула дисконтирования по смешанной схеме:
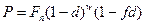 (68)
(68)
где w - целое число периодов дисконтирования по сложной учетной ставке, f - дробная часть периода, n = w+f.
• Формула дисконтирования по сложной учетной ставке, осущест-
вляемого несколько раз в год:
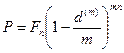 (69)
(69)
где n - число лет,
m - количество осуществлений операции дисконтирования в год.
• Формула дисконтирования по смешанной схеме при дисконтировании несколько раз в год:
 (70)
(70)
где n -числолет,
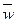 - целое число периодов дисконтирования в и годах,
- целое число периодов дисконтирования в и годах,
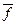 —дробная часть периода, n =
—дробная часть периода, n = 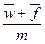
• Формула для определения срока ссуды (при использовании сложной учетной ставки):
 (71)
(71)
• Формулы для определения номинальной годовой учетной ставки:
 (72)
(72)
 (73)
(73)
где def - эффективная годовая учетная ставка.
■ Формулы определения эффективной годовой учетной ставки:
 (74)
(74)
 (75)
(75)
• Формула наращения сложными процентами по учетной ставке:
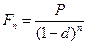 (76)
(76)
где n -число периодов начисления сложных процентов.
■ Формула наращения сложными процентами по учетной ставке при начислении процентов несколько раз в год:
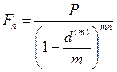 (77)
(77)
где n -числолет,
m - количество начислений в год.
Формула наращения непрерывными процентами:
F = Р*e  (78)
(78)
где  -силароста.
-силароста.
• Формула для определения срока ссуды (при непрерывном начислении процентов):
 (79)
(79)
Формула для определения силы роста:
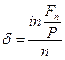 (80)
(80)
• Эквивалентность простых и сложных ставок:
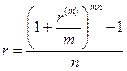 (81)
(81)
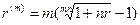 (82)
(82)
 (83)
(83)
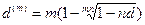 (84)
(84)
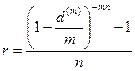 (85)
(85)
 (86)
(86)
 (87)
(87)
 (88)
(88)
где r, d - простые ставки.
• Эквивалентность сложных ставок:
 (89)
(89)
 (90)
(90)
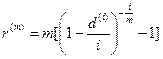 (91)
(91)
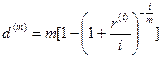 (92)
(92)
• Эквивалентность силы роста и простых ставок:
 (93)
(93)
 (94)
(94)
 (95)
(95)
 (96)
(96)
где r,d - простые ставки.
• Эквивалентность силы роста и сложных ставок:
 (97)
(97)
 (98)
(98)
 (99)
(99)
 (100)
(100)
• Формулы наращения сложными процентами с учетом уплаты налога:
а) если налог на все полученные проценты выплачивается один раз в конце срока:
 (101)
(101)
б) если налог на полученные проценты выплачивается каждый год:
 (102)
(102)
где q - ставка налога на проценты, а - коэффициент нармценям, рмний
либо 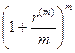 , либо
, либо  , либо
, либо 
• Формулы для вычисления величины налога за каждый год при наращении сложными процентами, если налог на полученные проценты выплачивается каждый год:
 (103)
(103)
где к - номер года, за который взимается налог.
• Формула наращения сложными или непрерывными процентами с учетом инфляции:
 (104)
(104)
где 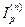 - индекс инфляции за период n, а равно
- индекс инфляции за период n, а равно
либо 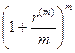 , либо
, либо  , либо
, либо  .
.
* Формула определения номинальной годовой процентной ставки, обеспечивающей в условиях инфляции реальную доходность согласно
первоначальной номинальной годовой ставке 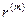 :
:
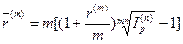 (105)
(105)
• Формула определении реальной номинальной годовой процентной ставки при объявленной исходной процентной ставке r (m) в условиях инфляции:
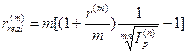 (106)
(106)
• Формула определения номинальной годовой учетной ставки, обеспечивающей в условиях инфляции реальную доходность согласно
первоначальной номинальной годовой ставке 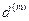

 (107)
(107)
• Формула определения реальной номинальной годовой учетной
ставки при объявленной исходной учетной Ставке d(m) в условиях инфляции:
 (108)
(108)
• Формула определения силы роста, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной силе роста  :
:
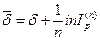 (109)
(109)
• Формула определения реальной силы роста при объявленной исходной силе роста  в условиях инфляции:
в условиях инфляции:

 (110)
(110)
Формула Фишера:
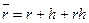 (111)
(111)
где А - годовой темп инфляции.
• Формула для вычисления величины нового платежа при использовании сложных ставок:
 (112)
(112)
где Р  и n
и n  - первоначальный платеж и срок его выплаты,
- первоначальный платеж и срок его выплаты,
n  - срок нового платежа, а равно либо
- срок нового платежа, а равно либо 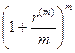 , либо
, либо  ,либо
,либо  .
.
• Формула для вычисления срока нового платежа при использовании сложных ставок:
 (113)
(113)
где Р  и n
и n  - первоначальный платеж и срок его выплаты;
- первоначальный платеж и срок его выплаты; 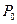 - величина нового платежа.
- величина нового платежа.
• Формула для определения величины консолидиромнного платежа при использовании сложных ставок:
 (114)
(114)
где Р  , P
, P  .....Р
.....Р  — платежи, выплачиваемые соответственно через время n
— платежи, выплачиваемые соответственно через время n  ,n
,n  …n
…n 
n  - срок консолидированного платежа.
- срок консолидированного платежа.
• Формула для определения срока консолидированного платежа при использовании сложных ставок:
 (115)
(115)
1пя где Р  , P
, P  , …, P
, …, P  - платежи, выплачиваемые соответственно через время n
- платежи, выплачиваемые соответственно через время n  ,n
,n  …n
…n 
P  - величина консолидированного платежа.
- величина консолидированного платежа.
• Будущая стоимость переменного аннуитета постнумерандо:
 (116)
(116)
• Приведенная стоимость переменного аннуитета постнумерандо:
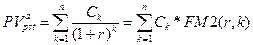 (117)
(117)
Будущая стоимость переменного аннуитета пренумерандо:
 (118)
(118)
• Приведенная стоимость переменного аннуитета пренумерандо:
 (119)
(119)
• Будущая стоимость постоянного срочного аннуитета постнуме-рандо:
 (120)
(120)
• Приведенная стоимость постоянного срочного аннуитета пост-нумерандо:
 (121)
(121)
• Оценка постоянного р -срочного аннуитета постнуыерандо:
а) будущая стоимость аннуитета:
 (122)
(122)
б) приведенная стоимость аннуитета:
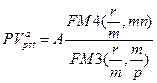 (123)
(123)
в) приведенная стоимость бессрочного аннуитета:
 (124)
(124)
где А - величина каждого денежного поступления;
r- ставка за базовый период начисления процентов;
m - количество начислений сложных процентов в периоде;
р - количество денежных поступлений в периоде;
n - количество периодов.
Приведенная стоимость постоянного отсроченного аннуитета постнумерандо:
PV  =A* vhFM4(r,n) = A * FM2(r,h) * FM4(r,n), (125)
=A* vhFM4(r,n) = A * FM2(r,h) * FM4(r,n), (125)
где v =  ;
;
h - число периодов, через которое начинает поступать первый из потока
платежей.
• Оценка постоянного р-срочного аннуитета пренумерандо:
а) будущая стоимость аннуитета:
 (126)
(126)
б) приведенная стоимость аннуитета:
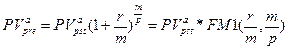 (127)
(127)
в) приведенная стоимость бессрочного аннунтета:
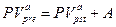 (128)
(128)
FV  ,PV
,PV  - будущая и приведенная стоимости соответствующих аннуитетов постнумерандо.
- будущая и приведенная стоимости соответствующих аннуитетов постнумерандо.
• Будущая стоимость постоянного р-срочного аннуитета постнумерандо с начислением простых процентов в течение периода:
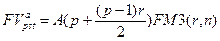 (129)
(129)
• Будущая стоимость постоянного р -срочного аннуитета пренумерандо с начислением простых процентов в течение периода:
 (130)
(130)
• Оценка постоянного аннуитета постнумерандо в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета:
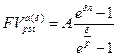 (131)
(131)
б) приведенная стоимость аннуитета:
 (132)
(132)
в) приведенная стоимость бессрочного аннуитета:
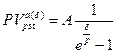 (133)
(133)
где А - величина каждого денежного поступления;
 - сила роста за базовый период начисления процентов;
- сила роста за базовый период начисления процентов;
р — количество денежных поступлений в периоде;
n — количество периодов.
• Оценка непрерывного аннуитета:
а) будущая стоимость аннуитета:
 (134)
(134)
б) приведенная стоимость аннуитета:
 (135)
(135)
в) приведенная стоимость бессрочного аннуитета:
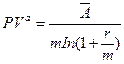 (136)
(136)
где 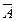 -суммарная величина денежных поступлений за базовый период начисления процентов.
-суммарная величина денежных поступлений за базовый период начисления процентов.
• Оценка непрерывного аннуитета в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета:
 (137)
(137)
б) приведенная стоимость аннуитета:
 (138)
(138)
в) приведенная стоимость бессрочного аннуитета:
 (139)
(139)
где 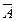 - суммарная величина денежных поступлений за базовый период
- суммарная величина денежных поступлений за базовый период
начисления процентов;
 - сила роста за базовый период начисления процентов.
- сила роста за базовый период начисления процентов.
• Оценка переменного аннуитета постнумерандо, платежи которого образуют арифметическую прогрессию:
а) будущая стоимость аннуитета:
 (140)
(140)
б) приведенная стоимость аннуитета:
 (141)
(141)
в) приведенная стоимость бессрочного аннуитета:
 (142)
(142)
где А - первый чльн прогрессии;
z - разность прогрессии.
• Оценка переменного аннуитета постнумерандо, платежи которого образуют геометрическую прогрессию:
а) будущая стоимость аннуитета:
 (143)
(143)
б) приведенная стоимость аннуитета:
 (144)
(144)
в) приведенная стоимость бессрочного аннуитета:
 (145)
(145)
где А — первый член прогрессии;
q - знаменатель прогрессии.
• Оценка постоянного аннуитета постнумерандо, период которого больше базового периода начисления процентов:
а) будущая стоимость аннуитета:
 (146)
(146)
б) приведенная стоимость аннуитета:
 (147)
(147)
в) приведенная стоимость бессрочного аннуитета:
 (148)
(148)
где А - величина каждого денежного поступления;
r - ставка за базовый период начисления процентов;
m — количество начислений сложных процентов в периоде;
u -количество периодов, через которое осуществляются денежныепоступления;
n —количество периодов...
• Оценка постоянного аннуитета постнумерандо, период которого больше базового периода начисления процентов, в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета:
 (149)
(149)
б) приведенная стоимость аннуитета:
 (150)
(150)
в) приведенная стоимость бессрочного аннуитета:
 (151)
(151)
где А - величина каждого денежного поступления;
 - сила роста за базовый период начисления процентов;
- сила роста за базовый период начисления процентов;
u - количество периодов, через которое осуществляются денежные поступления;
n - количество периодов.
• Оценка постоянного аннуитета пренумеракдо, период которого больше базового периода начисления процентов:
а) будущая стоимость аннуитета:
 (152)
(152)
б) приведенная стоимость аннуитета:
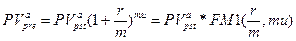 (153)
(153)
• Оценка постоянного аннуитета пренумерандо, период которого больше базового периода начисления процентов, в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета:
 (154)
(154)
б) приведенная стоимость аннуитета:
 (155)
(155)






