Электронная подпись на основе алгоритма RSA

Наи­бо­лее про­стым и рас­про­стра­нен­ным ин­ст­ру­мен­том элек­трон­ной под­пи­си яв­ля­ет­ся уже зна­ко­мый ал­го­ритм RSA. Ни­же оно бу­дет рас­смот­ре­на в ка­че­ст­ве при­ме­ра. Кро­ме это­го су­ще­ст­ву­ют еще десятки других схем цифровой подписи.

Предположим, что

d, p, q - секретные, а е, n = pq - открытые.

Замечания.

1. Разложение по n дает: j(n)=(p-1)(q-1); зная j(n) и e, можно найти d.

2. Из e и d можно найти кратность j(n); кратность j(n) позволяет определить делители n.

Пусть DATA - передаваемое сообщение от А к B.

А подписывает DATA для Б при передаче:

Ee_B,n_B { Ed_A,n_A {DATA}}.

При этом он использует:

­ закрытый ключ Ed_A,n_A А,

­ открытый ключ Ee_B,n_B B.

B может читать это подписанное сообщение сначала при помощи закрытого ключа Ed_В,n_В B с целью получения

Ed_A,n_A {DATA} = Ed_B,n_B {Ee_B,n_B {Ed_A,n_A {DATA}}}

и затем - открытого ключа Ee_A,n_A А для получения

DATA = Ee_A,n_A { Ed_A,n_A {DATA}}.

Таким образом, у B появляется сообщение DATA, посланное ему А.

Очевидно, что данная схема позволяет защититься от нескольких видов нарушений.

А не может отказаться от своего сообщения, если он признает, что секретный ключ известен только ему.

Нарушитель без знания секретного ключа не может ни сформировать, ни сделать осмысленное изменение сообщения, передаваемого по линии связи.

Данная схема позволяет при решении многих конфликтных ситуаций обходиться без посредников.

Иногда нет необходимости зашифровывать передаваемое сообщение, но нужно его скрепить электронной подписью. В этом случае текст шифруется закрытым ключом отправителя и полученная цепочка символов прикрепляется к документу. Получатель с помощью открытого ключа отправителя расшифровывает подпись и сверяет ее с текстом.

Известны модели цифровой подписи (digital signature) на основе алгоритмов симметричного шифрования, но при использовании систем с открытыми ключами цифровая подпись осуществляется более удобно.

Для использования алгоритма RSA сообщение следует сжать функцией хеширования (алгоритм MD5 - Message Digest Algorithm) до 256-битового хеша (H). Сигнатура сообщения S вычисляется следующим образом:

S = H mod n

Сигнатура пересылается вместе с сообщением.

Процесс идентификации заключается в получении хеш-функции сообщения (H') и сравнении с

H = S mod n

где H - хеш сообщения,

S - его сигнатура,

d - секретный ключ,

E - открытый ключ.

Проверке подлинности посвящены стандарты:

- проверка подлинности (аутентификация, authentication) - ISO 8730-90, ISO/IES 9594-90 и ITU X.509;

- целостность - ГОСТ 28147-89, ISO 8731-90;

Цифровая подпись - ISO 7498, P 34.10-94 (Россия), DSS (Digital Signature Standard, США).

Цифровая сигнатура

Часто возникают ситуации, когда получатель должен уметь доказать подлинность сообщения внешнему лицу. Чтобы иметь такую возможность, к передаваемым сообщениям должны быть приписаны так называемые цифровые сигнатуры.

Цифровая сигнатура - это строка символов, зависящая как от идентификатора отправителя, так и содержания сообщения.

 

 

 

Рисунок 4.1 - Цифровая сигнатура

Ни­кто при этом кро­ме поль­зо­ва­те­ля А не мо­жет вы­чис­лить циф­ро­вую сиг­на­ту­ру А для кон­крет­но­го со­об­ще­ния. Ни­кто, да­же сам поль­зо­ва­тель не мо­жет из­ме­нить по­слан­но­го со­об­ще­ния так, что­бы сиг­на­ту­ра ос­та­лась не­из­мен­ной. Хо­тя по­лу­ча­тель дол­жен иметь воз­мож­ность про­ве­рить яв­ля­ет­ся ли циф­ро­вая сиг­на­ту­ра со­об­ще­ния под­лин­ной. Что­бы про­ве­рить циф­ро­вую сиг­на­ту­ру, поль­зо­ва­тель В дол­жен пред­ста­вить по­сред­ни­ку С ин­фор­ма­цию, ко­то­рую он сам ис­поль­зо­вал для ве­ри­фи­ка­ции сиг­на­ту­ры.

Ес­ли по­ме­чен­ное сиг­на­ту­рой со­об­ще­ние пе­ре­да­ет­ся не­по­сред­ст­вен­но от от­пра­ви­те­ля к по­лу­ча­те­лю, ми­нуя про­ме­жу­точ­ное зве­но, то в этом слу­чае идет речь об ис­тин­ной циф­ро­вой сиг­на­ту­ре.

Рас­смот­рим ти­пич­ную схе­му циф­ро­вой сиг­на­ту­ры.

Пусть Е - функция симметричного шифрования и f - функция отображения некоторого множества сообщений на подмножество мощности р из последовательности {1,..., n }.

Например р=3 и n =9. Если m - сообщение, то в качестве f можно взять функцию f (m) = {2, 5, 7}.

Для каждого сообщения пользователь А выбирает некоторое множество ключей K =[ K ₁,..., K _n} и параметров V={v₁,...,v_n} для использования в качестве пометок сообщения, которое будет послано В. Множества V и V’={E(v₁, K ₁)..., E(v_n, K _n)} посылаются пользователю В и заранее выбранному посреднику С.

Пусть m - сообщение и idm - объединение идентификационных номеров отправителя, получателя и номера сообщения. Если f( {idm, m }), то цифровая сигнатура m есть множество K ’=[ K _i,..., K _j}. Сообщение m, идентификационный номер idm и цифровая сигнатура К’ посылаются В.

 

 

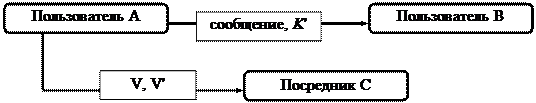Рисунок 4.2 – Использование посредника

Получатель В проверяет сигнатуру следующим образом. Он вычисляет функцию f( {idm, m }) и проверяет ее равенство К’. Затем он проверяет, что подмножество {v_i,...,v_j} правильно зашифровано в виде подмножества {E(v_i, K _i)..., E(v_j, K _j)} множества V’.

В кон­фликт­ной си­туа­ции В по­сы­ла­ет С сообщение m, иден­ти­фи­ка­ци­он­ный но­мер idm и мно­же­ст­во клю­чей K ’, ко­то­рое В объ­яв­ля­ет сиг­на­ту­рой m. То­гда по­сред­ник С так же, как и В, бу­дет спо­со­бен про­ве­рить сиг­на­ту­ру. Ве­ро­ят­ность рас­кры­тия двух со­об­ще­ний с од­ним и тем же зна­че­ни­ем функ­ции f долж­на быть очень ма­ла. Что­бы га­ран­ти­ро­вать это, чис­ло n долж­но быть дос­та­точ­но боль­шим, а чис­ло р долж­но быть боль­ше 1, но мень­ше n.

Ряд не­дос­тат­ков этой мо­де­ли оче­ви­ден:

­ долж­но быть третье ли­цо - по­сред­ник, ко­то­ро­му до­ве­ря­ют как по­лу­ча­тель, так и от­пра­ви­тель;

­ по­лу­ча­тель, от­пра­ви­тель и по­сред­ник долж­ны об­ме­нять­ся су­ще­ст­вен­ным объ­е­мом ин­фор­ма­ции, пре­ж­де чем бу­дет пе­ре­да­но ре­аль­ное со­об­ще­ние;

­ пе­ре­да­ча этой ин­фор­ма­ции долж­на осу­ще­ст­в­лять­ся в за­кры­том ви­де;

­ эта ин­фор­ма­ция ис­поль­зу­ет­ся край­не не­эф­фек­тив­но, по­сколь­ку мно­же­ст­ва K, V, V’ ис­поль­зу­ют­ся толь­ко один раз.

Тем не ме­нее, да­же та­кая схе­ма циф­ро­вой сиг­на­ту­ры мо­жет ис­поль­зо­вать­ся в ин­фор­ма­ци­он­ных сис­те­мах, в ко­то­рых не­об­хо­ди­мо обес­пе­чить ау­тен­ти­фи­ка­цию и за­щи­ту пе­ре­да­вае­мых со­об­ще­ний.

Использование цифровой сигнатуры предполагает использование некоторых функций шифрования:

S = H(k, T),

где S - сигнатура, k - ключ, T - исходный текст.

Функция H(k, T) - является хэш-функцией, если она удовлетворяет следующим условиям:

1) исходный текст может быть произвольной длины;

2) само значение H(k, T) имеет фиксированную длину;

3) значение функции H(k, T) легко вычисляется для любого аргумента;

4) восстановить аргумент по значению с вычислительной точки зрения - практически невозможно;

функция H(k, T) – однозначна

При этом разделяют слабую и сильную однозначность. При слабой однозначности для заданного значения T практически невозможно отыскать другой текст Т’, для которого H(k, T) = H(k, T’). При сильной однозначности для любого текста T невозможно найти другой подходящий текст, имеющий то же значение хэш-функции

Из определения следует, что для любой хэш-функции есть тексты-близнецы - имеющие одинаковое значение хэш-функции, так как мощность множества аргументов неограниченно больше мощности множества значений. Такой факт получил название «эффект дня рождения». (Факт теории вероятностей: в группе из 23 человек с вероятностью больше 0.5 два и более человека родились в одно и то же число)

Наиболее известные из хэш-функций - MD2, MD4, MD5 и SHA.

Три алгоритма серии MD разработаны Ривестом в 1989-м, 90-м и 91-м году соответственно. Все они преобразуют текст произвольной длины в 128-битную сигнатуру.

Алгоритм MD2 предполагает:

­ дополнение текста до длины, кратной 128 битам;

­ вычисление 16-битной контрольной суммы (старшие разряды отбрасываются);

­ добавление контрольной суммы к тексту;

­ повторное вычисление контрольной суммы.

Алгоритм MD4 предусматривает:

­ дополнение текста до длины, равной 448 бит по модулю 512;

­ добавляется длина текста в 64-битном представлении;

­ 512-битные блоки подвергаются процедуре Damgard-Merkle, причем каждый блок участвует в трех разных циклах. (В отличие от хэш-функции - этот класс преобразований предполагает вычисление для аргументов фиксированной длины также фиксированных по длине значений)

 

Задание к лабораторной работе

Студенты, имеющие четный вариант по журналу, реализуют шифрование файлов с помощью алгоритма RSA.

Студенты, имеющие нечетный вариант по журналу, реализуют ЭЦП на базе RSA.

Контрольные вопросы к лабораторной работе:

1. Какие асимметричные алгоритмы шифрования Вы знаете?

2. Какие системы асимметричные или симметричные являются более криптостойкими, почему?

3. В чем отличие арбитражной электронной цифровой подписи от обычной.

4. Назначение сигнатуры? Использование сигнатурного подхода при реализации ЭЦП.

Лабораторная работа №5

Тема: Стеганографические методы защиты информации.

Цель работы: Изучение стеганографических методов защиты информации. Реализация программы с использованием стеганографических принципов защиты информации.