Основы термодинамики. Адиабатический процесс. Циклические процессы

1. Кислород, занимающий объем V ₁ = 5 л при давлении р ₁ = 1 МПа, изотермически сжимается в 3 раза. Определить конечное давление р ₂ и работу А, совершенную газом.

2. Газ массой m = 10 г расширяется изотермически от объёма V ₁ до объёма V ₂ = 2 V ₁. Чему равна наиболее вероятная скорость молекул газа, если работа расширения газа А = 900 Дж.

3. Некоторый газ массой 5 г расширяется изотермически от объема V ₁ до объема V ₂=2 V ₁. Работа расширения равна 1 кДж. Определить среднюю квадратичную скорость молекул.

4. Некоторый газ массой 1 кг находится при температуре Т =300 К и под давлением р₁=0,5 МПа. В результате изотермического сжатия давление газа увеличилось в 2 раза. Работа, затраченная на сжатие А =-432 кДж. Определить: 1) какой это газ; 2) первоначальный удельный объем газа.

5. Для изобарического нагревания ν = 5 молей идеального газа от температуры Т ₁ = 273 К до Т ₂ = 373 К потребовалось сообщить газу теплоту Q = 14,54 кДж. Определить число степеней свободы молекул газа.

6. Водород массой m = 10 г нагрели на Δ T = 200 К, причем газу было передано количество теплоты Q = 40 кДж. Найти изменение Δ u внутренней энергии газа и совершенную им работу А. М = 2·10^-3 кг/моль.

7. Азот массой 2 кг охлаждают при постоянном давлении от 400 до 300 К. Определить изменение внутренней энергии, внешнюю работу и количество выделенной теплоты.

8. Азот массой m = 280 г расширяется изобарно при давлении P = 1 МПа. Определить работу расширения и конечный объём газа, если на расширение затрачена теплота Q = 5 кДж, а начальная температура азота Т ₁ = 290 К.

9. При изобарном нагревании некоторого идеального газа в количестве ν = 2 моль на Δ T = 90 К ему было сообщено количество теплоты 5,25 кДж. Определить работу, совершённую газом, изменение внутренней энергии и коэффициент Пуассона газа.

10. Для изобарного нагревания ν молей идеального газа от температуры Т ₁ до температуры Т ₂ потребовалось сообщить ему количество теплоты, равное Q. Определить показатель адиабаты газа.

11. 20 г водорода, имеющего температуру 300 К, сначала расширили адиабатно, увеличив объем в 5 раз, а затем сжали изотермически до первоначального объема. Найти температуру после адиабатного расширения и работу, совершенную в итоге газом.

12. 1 моль воздуха, имевший температуру 0°С и находившийся под давлением 5 кПа, адиабатически расширился до давления 1 кПа. На сколько градусов понизилась температура воздуха в результате расширения? Какую работу совершил газ при расширении?

13. При адиабатном сжатии кислорода массой m = 20 г его внутренняя энергия увеличилась на Δ U = 8 кДж и температура повысилась до Т ₂ = 900 К. Найти, на сколько повысилась температура Δ T и каково конечное давление газа P ₂, если начальное давление Р ₁ = 200 кПа.

14. Азот массой m = 1 кг занимает при температуре Т ₁ = 300 К объём V ₁ = 0,5 м³. В результате адиабатического сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа, его конечную температуру и изменение внутренней энергии.

15. Азот массой m = 2 г, имеющий температуру T ₁ = 300 К, был адиабатно сжат так, что его объем уменьшился в n = 10 раз. Определить конечную температуру T ₂ газа и работу А сжатия.

16. Азот массой m = 1 кг занимает при температуре T ₁= 300 К объем V ₁= 0,5 м³. В результате адиабатического сжатия давление газа увеличилось в 3 раза. Определить: 1) конечный объем газа; 2) его конечную температуру; 3) изменение внутренней энергии газа. М = 28·10^-3 кг/моль.

17. Кислород массой m = 64 г, занимающий объем V ₁ = 0,5 л при давлении р ₁= 1 МПа, расширяется в n = 3 раза. Определите конечное давление и работу, совершенную газом, если процесс адиабатический.

18. При адиабатном расширении 64 г кислорода, вначале находившемся при нормальных условиях, его объем увеличился в 3 раза. Найти изменение внутренней энергии газа и совершенную им работу.

19. В цилиндре под поршнем находится водород массой 20 г при температуре . Водород начал расширяться адиабатно, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатного расширения и работу , совершенную газом.

20. Над молем идеального газа совершается замкнутый цикл,

состоящий из двух изохор и двух изобар. Температуры в точках 1 и 3 равны Т 1 и Т 2. Определить работу, совершенную газом за цикл, если известно, что точки 2 и 4 лежат на одной изотерме.

21. Один моль одноатомного газа совершает цикл, состоящий из двух изохор и двух изобар. При этом максимальный объем в 3 раза больше минимального, а максимальное давление в 2 раза больше минимального. Определить КПД цикла.

22. Кислород совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление в 2 раза больше наименьшего, а наибольший объем в 4 раза больше наименьшего. Определить термический КПД цикла.

23. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатического расширения объем газа увеличивается в n = 4 раза. Определить термический к.п.д. цикла.

24. Кислород, занимающий объём V ₁ = 5 л при давлении p ₁ = 1 МПа, расширяется в n = 3 раза. Определите конечное давление и работу, совершённую газом, если процесс изотермический. Чему равно изменение энтропии газа, если его масса 64 г?

25. 64 г кислорода изобарно нагрели так, что его объем увеличился в 2 раза, а затем изохорно охладили так, что давление упало в 2 раза. Определить приращение энтропии газа.

26. Азот, занимавший объём V ₁ = 10 л под давлением P ₁ = 0,2 МПа, изотермически расширился до объёма V ₂ = 28 л. Определить работу А расширения газа, количество теплоты Q, полученное газом и изменение энтропии одного моля газа.

27. Кислород массой m = 10 г нагревают от температуры t ₁ = 50°С до температуры t ₂ = 150°С. Найти приращение Δ S энтропии, если нагревание происходит: а) изохорически; б) изобарически.

28. Водород массой m = 100 г был изобарно нагрет так, что его объем увеличился в 3 раза, затем этот водород был изохорно охлажден так, что его давление уменьшилось 3 раза. Найти изменение энтропии в ходе указанных процессов.

29. Как изменится энтропия 2 г водорода, занимающего объем 40 л при температуре 270 К, если давление увеличить вдвое при постоянной температуре, а затем изохорно повысить температуру до 320К? Молярная масса водорода равна 0,002 кг/моль.

30. 1,7 г гелия адиабатически расширили до втрое большего объема, а затем изобарно сжали до первоначального объема. Чему равно изменение энтропии газа за весь процесс?

31. Идеальный одноатомный газ (ν = 2 моль) сначала изобарно нагревали, так что объем газа увеличился в n ₁ = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в n ₂= 2 раза. Определить приращение энтропии в ходе указанных процессов.

32. Давление v молей газа в некотором процессе изменяется прямо пропорционально его объему. Найти изменение энтропии газа при увеличении его объема в n раз, если его показатель адиабаты равен γ.

33. Процесс расширения двух молей аргона происходит так, что давление газа увеличивается прямо пропорционально его объему. Найти изменение энтропии газа при увеличении его объема в два раза.

34. Найти изменение энтропии Δ S при переходе массы m = 8 г кислорода от объема V ₁ = 10 л к объему V ₂ = 40 л при температуре Т = 353 К.

35. Найти изменение энтропии Δ S при переходе массы m = 8 г кислорода от объёма V ₁ = 10 л при температуре t ₁=80ºC к объёму V ₂ = 40 л при температуре t ₂ = 300ºC.

36. Чему равно изменение энтропии 8 г кислорода при расширении от объема 10 л до объема 40 л, если начальная температура равна 30°С, а конечная – 300°С?

37. Найти изменение энтропии Δ S при превращении массы m = 10 г льда (t = – 20ºС) в пар (t = 100ºС). С _л = 2100 Дж/кг·К, λ = 335 кДж/кг, С _в = 4200 Дж/кг·К, τ = 2,3 МДж/кг.

38. Лед массой 2 кг, находящийся при температуре -13⁰С, нагрели до 0⁰С и расплавили. Определить изменение энтропии. (λ=3,35^.10⁵ Дж/кг, С_льда=2,1^.10³ Дж/(кг^.К))

39. Лед массой 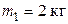при температуре был превращен в воду той же температуры с помощью пара, имеющего температуру . Определить массу израсходованного пара. Каково изменение 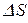энтропии системы лед-пар? , , .

40. Кусочек меди массы 300 г, имеющий температуру , поместили в калориметр, в котором находится 100 г воды при . Найти изменение энтропии системы за время выравнивания температуры. Теплоемкостью калориметра можно пренебречь. , .

41. Смешали воду массой m ₁ = 5 кг при температуре Т ₁ = 280 К с водой m ₂ = 8кг при температуре Т ₂ = 350 К. найти: 1) температуру Т смеси; 2) изменение энтропии ΔS, произошедшее при смешивании. Удельная теплоемкость воды с = 4200 Дж/кг.

42. Определить удельную теплоемкость С_Р смеси кислорода и гелия, если количество вещества ν₁ первого компонента равно 2 моль, а количество вещества ν₂ второго равно 4 моль.

43. Чему равна удельная теплоемкость при постоянном объеме смеси из 3-х молей неона и 2-х молей гелия, молярные массы которых равны соответственно 20 г/моль и 4 г/моль?

44. Вычислить удельную теплоёмкость С _V смеси неона и водорода. Массовые доли газов соответственно равны w ₁ = 0,8 и w ₂ = 0,2. М ₁ = 20·10^-3 кг/моль, М ₂ = 2·10^-3 кг/моль.

45. В баллоне находятся гелий и азот. Определить удельную теплоемкость с_V смеси этих газов, если массовые доли гелия и азота одинаковы и равны 0,5. Молярные массы гелия и азота равны соответственно 4 г/моль и 28 г/моль

46. Газовая смесь состоит из азота массой 2 кг и аргона массой 1 кг. Принимая газы за идеальные, определить удельные теплоемкости С _Vи С_Р газовой смеси. М _азота = 28·10^-3 кг/моль, М _аргона = 40·10^-3 кг/моль.

47. Вычислить постоянную Пуассона для газовой смеси, состоящей из двух молей кислорода и трех молей углекислого газа. М ₁ = 32·10^-3 кг/моль, М ₂ = 44·10^-3 кг/моль.

48. Определите коэффициент Пуассона γ для смеси газов, содержащей гелий массой m ₁ = 8 г и водород массой m ₂ = 2 г. М ₁ = 4·10^-3 кг/моль, М ₂ = 2·10^-3 кг/моль.

49. Чему равен коэффициент Пуассона для газовой смеси, состоящей из 7 г азота и 20 г гелия. М _аз = 28·10^-3 кг/моль, М _г = 4·10^-3 кг/моль.