1. По гладкой наклонной доске пустили катиться снизу вверх маленький брусок. На расстоянии l = 30 см брусок побывал дважды: через t 1 = 1 с и через t 2 = 2 c после начала движения. Определить начальную скорость бруска υ 0.
2. С башни брошен камень в горизонтальном направлении с начальной скоростью 40 м/с. Какова скорость камня через 3 с после начала движения? Какой угол образует вектор скорости камня с плоскостью горизонта в этот момент.
3. На толкание ядра, брошенного с высоты h = 1,8 м под углом α = 30º к горизонту, затрачена работа А = 216 Дж. Через какое время t и на каком расстоянии s от места бросания ядро упадёт на землю? Масса ядра m = 2 кг.
4. Тело брошено горизонтально со скоростью v 0= 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через t = 2 с после начала движения.
5. Снаряд вылетел со скоростью 30 м/с под углом 60° к горизонту. Чему равен радиус кривизны траектории снаряда через 2 с после выстрела?
6. Мяч брошен со скоростью 10 м/с под углом 45° к горизонту. Найти радиус кривизны траектории мяча через 1 с после броска.
7. Мяч брошен со скоростью υ0 под углом α к горизонту. Найти υ0 и α, если максимальная высота подъема мяча h = 3 м, радиус кривизны траектории мяча в этой точке R = 3 м.
8. Под каким углом к горизонту надо бросить тело, чтобы центр кривизны его траектории в вершине находился на земле?
9. Диск радиусом 10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 0,5 рад/с2. Найти касательное, нормальное и полное ускорение точек на окружности диска в конце второй секунды после начала вращения.
10. Диск радиусом R =10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением υ= At + Bt 2 (А =0,3 м/с2, В = 0,1 м/с3). Определить момент времени, для которого вектор полного ускорения  образует с радиусом колеса угол φ=40.
образует с радиусом колеса угол φ=40.
11. Материальная точка начинает движение по окружности радиуса 12,5 см с постоянным тангенциальным ускорением 0,5 см/с2. Определить момент времени, в который угол между векторами ускорения и скорости равен 45° и путь, пройденный точкой до этого момента.
12. Материальная точка начинает двигаться по окружности радиусом r = 12,5 см с постоянным тангенциальным ускорением aτ = 0,5 см/с2. Определить: 1) момент времени, когда вектор ускорения  образует с вектором скорости
образует с вектором скорости  угол α = 45°; 2) величину перемещения к этому моменту.
угол α = 45°; 2) величину перемещения к этому моменту.
13. Материальная точка движется в плоскости по закону:  , где
, где 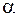 и
и  – положительные постоянные. Найти момент времени, когда угол между скоростью и ускорением будет равен 45°.
– положительные постоянные. Найти момент времени, когда угол между скоростью и ускорением будет равен 45°.
14. Зависимость угла поворота от времени для точки, лежащей на ободе колеса радиуса R, задается уравнением  , где A =1 рад/c3, B =0,5 рад/c2, C =2 рад/c, D =1 рад. К концу третьей секунды эта точка получила нормальное ускорение, равное 153 м/с2. Определить радиус колеса.
, где A =1 рад/c3, B =0,5 рад/c2, C =2 рад/c, D =1 рад. К концу третьей секунды эта точка получила нормальное ускорение, равное 153 м/с2. Определить радиус колеса.
15. Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением S = At 3, где А =0,1 см/с3. Найти нормальное (аn) и тангенциальное (а τ) ускорения точки в момент, когда линейная скорость точки υ = 0,3 м/с.
16. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а τ. Найти тангенциальное ускорение а τ точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки υ = 79,2 см/с.
17. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R = 10 м. Уравнение движения автомобиля  (м/с2). (
(м/с2). ( -означает криволинейную координату, отсчитанную от некоторой начальной точки на окружности). Найти полное ускорение a в момент времени t = 5 с.
-означает криволинейную координату, отсчитанную от некоторой начальной точки на окружности). Найти полное ускорение a в момент времени t = 5 с.
18. Точкадвижется по окружности радиусом R = 2 м согласно уравнению S = At 3, где А = 2 м/с3. В какой момент времени t нормальное ускорение аn будет равно тангенциальному аτ? Определить полное ускорение в этот момент времени. (S – путь, проходимый телом).






