Поскольку появление того или иного значения 
в процессе измерения является случайным событием, необходимо ввести понятие вероятности события (математической), как количественной меры объективной возможности появления данного события. Событием назовем результат опыта. Если событие достоверное, т.е. всегда наступающее в результате опыта, то его вероятность равна 1. Вероятность невозможного события, т.е. никогда не наступающего в результате опыта равно нулю. Поэтому вероятность любого события лежит в промежутке [0;1].
Пусть 
– число измерений, а 
– число результатов, попадающих в заданный промежуток значений, тогда вероятность события есть предел отношения этих величин при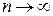 
:
. (1.1)
Плотностью вероятности 
назовём отношение вероятности того, что значение величины попадает в заданный интервал, к ширине этого интервала значений:
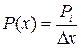. (1.2)
Плотность вероятности возникновения значения xi, как правило, определяется законом нормального распределения Гаусса:
, (1.3)
где 
– средняя квадратичная погрешность, определяемая дисперсией D (разброс) распределения
. (1.4)
График функции распределения показан на рис.10, откуда видно, что гауссова кривая имеет симметричный колоколообразный вид, характеризуемый двумя параметрами: положением вершины – 
, 2 – расстоянием между точками перегиба. Здесь – характеризует степень влияния случайных погрешностей на результаты измерения: чем меньше , тем уже гауссова кривая.
Рис.10. График функции распределения
Для каждой серии измерений среднее арифметическое будет различным, и само будет являться случайной величиной, определяемой выражением
. (1.5)
Так как 
, то значение должно лежать в некоторых пределах значений вблизи 
. Назовем доверительным интервалом интервал значений [ 
; 
], в который истинное значение попадает с заданной вероятностью. Доверительной вероятностью (надежностью) - называется вероятность того, что истинное значение измеряемой величины попадает в заданный доверительный интервал. Чем больше ширина доверительного интервала, тем с большей вероятностью искомая величина попадает в этот интервал. При конечном числе измерений 
заменяют его приближенным значением 
, называемым средним квадратичным отклонением среднего арифметического:
. (1.6)
Если систематическими погрешностями можно пренебречь, то при числе измерений 
с доверительной вероятностью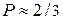 
можно считать 
. Для более точного нахождения доверительного интервала вводят коэффициент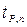 
, зависящий от числа измерений и доверительной вероятности.
