ВВЕДЕНИЕ
В ЛАБОРАТОРНЫЙ ПРАКТИКУМ
Цель работы: Ознакомление с методами оценки результатов измерений
и расчета погрешностей.
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
Физические величины и их измерение
Свойства, присущие объектам материального мира, могут быть охарактеризованы физическими величинами.
Физическая величина – характеристика процессов и явлений материального мира, сходных качественно, но различных количественно.
Одинаковые свойства различных материальных объектов количественно характеризуются численными значениями физических величин, определяемыми путем измерений.
Измерение – это операция сравнения данной физической величины с величиной ей однородной, принятой за единицу измерения или эталон.
За эталон принимают образец или меру физической величины, предназначенную для хранения единицы величины. Под однородными физическими величинами понимают величины, характеризующие одно и то же свойство разных объектов, например, длина стола и диаметр диска.
Любое измерение состоит из следующих элементов:
1)получение объекта измерения;
2)выявление измеряемой величины;
3)выбор технических средств измерения;
4)разработка методики измерения;
5)выполнение измерений;
6)анализ результатов измерения;
7)нахождение погрешности измерения.
По способу получения значения измеряемой величины можно выделить прямые и косвенные измерения.
Прямым измерением называется нахождение значения физической величины непосредственно из опытных данных с помощью измерительных приборов.
Косвенным измерением называется нахождение значения физической величины из известной связи данной величины с величинами, подвергаемым прямым измерениям.
Примером прямого измерения может служить измерение длины с помощью линейки, времени с помощью секундомера и т.д. Примером косвенных измерений может служить нахождение сопротивления из закона Ома из измеренных значений падения напряжения и силы тока. Косвенные измерения используют в случае, если невозможно по каким-либо причинам использовать прямые измерения искомой величины, или когда прямое измерение дает менее точный результат.
Погрешности измерений
В процессе измерения мы стремимся получить наиболее точное значение величины, однако результат измерения любой физической величины не совпадает с ее истинным значением. Это происходит вследствие различных причин.
В зависимости от причин возникновения, погрешности можно классифицировать следующим образом:
1) погрешности метода измерения – возникающие вследствие несовершенства применяемого метода измерения, из-за наличия допущений и упрощений, применяемых в эмпирических формулах;
2) погрешности инструментальные – возникают при использовании измерительных приборов и эталонов;
3) погрешности, возникающие в результате неправильной установки прибора;
4) погрешности, возникающие вследствие внешнего влияния на объект измерения (температура, влажность, давление, различные поля);
5) субъективные погрешности – обусловленные индивидуальными особенностями наблюдателя;
6) погрешности отсчитывания – погрешности, которые в основном появляются вследствие округления показаний измерительных приборов до заданной степени точности.
По форме представления различают абсолютные и относительные погрешности.
Отклонение результата измерения от истинного значения физической величины называют абсолютной погрешностью измерения.
Отношение абсолютной погрешности к истинному значению измеряемой величины называют относительной погрешностью (см. п. 5).
По характеру отклонений от истинного значения выделяют три вида погрешности:
1) Промахи – это грубые ошибки, обусловленные недостатком внимания и тщательности в работе и др. причинами.
2) Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях данной величины.
3) Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях данной величины.
Промахи обычно вызваны неправильными действиями наблюдателя, поэтому их следует отбрасывать. Систематические погрешности в основном вызваны приборами и характеризуются постоянством знака.
Случайные погрешности являются погрешностями, природу которых мы не знаем, но можем учесть при неоднократных измерениях с помощью математической статистики и теории вероятностей.
Методика расчета случайных погрешностей прямых измерений
Измерим 
раз некоторую физическую величину 
при одинаковых условиях и получим набор значений 
, 
, 
,..., 
.
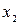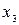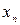Найдём среднее арифметическое значение величины по формуле:
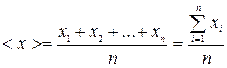(1)
Чтобы увеличить точность измерений их проводят многократно. При большом числе измерений (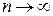
) среднее арифметическое значение измеряемой величины будет стремиться к её истинному значению. При конечном числе они будут равны друг другу лишь приближенно, поэтому необходимо определять степень этого приближения.
Найдем среднее квадратичное отклонение среднего арифметического (см. прил.1):
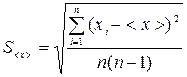. (2)
При этом значение случайной погрешности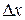 
в случае небольшого числа измерений можно представить в виде
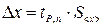, (3)
где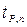 
- коэффициент Стьюдента, зависящий от доверительной вероятности 
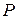(см. прил.1) и числа измерений . Значения коэффициента Стьюдента для доверительной вероятности 
приведены в таблице 1.
Таблица 1
Значения коэффициента Стьюдента.
| Число измерений,
| |||||||||
| Коэффициент
Стьюдента,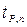
| 12.71 | 4.30 | 3.18 | 2.77 | 2.57 | 2.45 | 2.36 | 2.31 | 2.26 |
