Линейная независимость векторов, составляющих ортонормированную систему

Система векторов e₁, e₂, …, e_n евклидова пространства называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину. Пример: a₁=(0,1), a₂=(1,0)

В ортонормиров. сист. векторы ортогональны по определению. Докажем, что они ЛНЗ. Предположим противное, тогда , где не все «лямбда» равны 0. Пусть Умножим рав-во по правилу скалярного произв-ия на а₁. Т.к. векторы взаимно ортогональны, т.е. (a_i,a_j)=0 и т.к. (0,а₁)=0, мы получим: , то (a₁,a₁)=0, и, следовательно, a₁ =0, что противоречит условию (векторы ненулевые).

Итак, 3 вектора пространства ЛНЗ, следовательно, они являются базисом.

Формула для вычисления координат вектора в ортогональном базисе.

Если и взаимно перпендикулярны и их модули равны единице, то базис называется ортонормированным, и мы получим известную нам прямоугольную декартову систему координат на плоскости.

Итак, пусть – произвольный базис, и – любые два вектора. Рассмотрим скалярное произведение этих векторов и преобразуем его, используя ранее доказанные свойства:

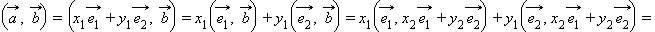
Таким образом, для вычисления скалярного произведения двух векторов в произвольном базисе, кроме их координат, надо знать модули базисных векторов и угол между ними. Очевидно, что если базис ортонормирован, то 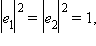и мы получим известную формулу для скалярного произведения в ортогональной декартовой системе координат.

 

Невырожденность ортогональной матрицы

Матрица А порядка n*n называется невырожденной, если ее строки линейно независимы, в противном случае – вырожденная.

Теорема: квадратная матрица А невырождена тогда и только тогда, когда ее определитель |А| не равен нулю.

Квадратная матрица A называется ортогональной, если соответствующая ей система векторов столбцов является ортонормированной.

(a_i,a_j)=∑_k=1ⁿa_kia_kj= δ_ij

Пусть A - ортогональная матрица.

A^T=A^-1 –необходимое и достаточное условие ортогональности матрицы A.

A^TA=E (по определению), A^-1A=E.

А т.к. обратная матрица существует, если А невырожденная, то ортогональная матрица является невырожденной.

Изменение матрицы линейного преобразования при замене базиса.

Пусть -- линейное преобразование пространства , и -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда

Доказательство. Пусть -- произвольный вектор пространства , -- его образ, то есть . Пусть и 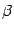-- координатные столбцы векторов и в старом базисе, а , -- в новом. Тогда в силу формулы . Имеем 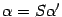, . Подставим эти выражения в предыдущую формулу, получаем . Откуда 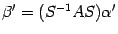. С другой стороны, в силу формулы в новом базисе . Сравнивая это равенство с предыдущим, получаем .