Неравенство Коши-Буняковского.
Для любых двух векторов в евклидовом пространстве справедливо неравенство

Доказательство:
 , x-произвольное число
, x-произвольное число
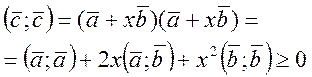
по свойству положительной определенности скалярного произведения

Неравенство треугольника.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.
|
Линейная независимость лестничной системы векторов.
Система векторов в Rn:
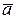 = (a1, a2, a3 … an)
= (a1, a2, a3 … an)
 = (0, b2, b3 … bn)
= (0, b2, b3 … bn)
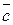 = (0, 0, c3 … cn)
= (0, 0, c3 … cn)
Теорема: любая лестничная система векторов линейно независима.
Доказательство: Предположим противное. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть, например, 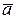 линейно выражается через
линейно выражается через  ,
, 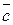 …
…
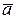 =k
=k  +l
+l 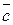 …
…
Но такое равенство невозможно, поскольку первая координата вектора 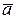 отлична от нуля, а первая координата вектора k
отлична от нуля, а первая координата вектора k  +l
+l 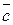 … равно нулю. Полученное противоречие доказывает, что система
… равно нулю. Полученное противоречие доказывает, что система 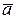 ,
,  ,
, 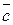 , … линейно независима.
, … линейно независима.
Однозначность разложения вектора по базису.
Теорема о базисе. Любая ЛНЗ система векторов из Rn явл. базисом Rn, когда число векторов этой системы равно n.
Док-во. Пусть: { в1, в2, …, вm } ЛНЗ система в Rn, докажем, что m=n 1) m>n. Получим, что система ЛЗ(по теореме об ортогональном векторе), что противоречит условию; 2) m<n Пусть{ в1, в2, …, вm }- базис Rn, то для любого Х ЄRn х=х1в1+х2в2+…+хmвm; m<n,то по теореме о существовании ортогонального вектора есть ненулевой вектор, кот. Ортогонален любому вектору этой системы (у╨вi, i=1,…,n), то увi=0; у ЄRn, тогда у=у1в1+у2в2+…+уmвm, умножим это рав-во на само себя уу=(у1в1+у2в2+…+уmвm)у=у1(в1у1)+у2(у2в2)+…+уm(уmвm)=0; уу=0, то у=0, а по усл теоремы у≠0, противоречие, значит m<n неверно, тогда m=n.
5. Формула умножения комплексных чисел в тригонометрической форме.
Z1=| Z1|(cosφ1 + i sinφ1); Z2=| Z2|(cosφ2 + i sinφ2)
Z1 · Z2 =| Z1|| Z2|((cosφ1 cosφ2 - sinφ1 sinφ2 ) + i(sinφ1 cosφ2 + cosφ1 sinφ2)) =
| Z1|| Z2|(cos(φ1+ φ2) + i sin(φ1 + φ2));
Для умножения Z1 на Z2 модули этих чисел следует перемножить, а аргументы сложить.
Формула деления комплексных чисел в тригонометрической форме.
Z1=| Z1|(cosφ1 + i sinφ1); Z2=| Z2|(cosφ2 + i sinφ2)
 φ1-φ2) + isin (φ1-φ2)) Z2≠0
φ1-φ2) + isin (φ1-φ2)) Z2≠0
Для нахождения частного  следует модуль числа Z1 разделить на модуль числа Z2, а из аргумента числа Z1 вычесть аргумент числа Z2.
следует модуль числа Z1 разделить на модуль числа Z2, а из аргумента числа Z1 вычесть аргумент числа Z2.
Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений.
Теорема: Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство: применим к системе
A11X1 + A12X2
8. Теорема о пространстве решений однородной системы линейных алгебраических уравнений.
Теорема о линейности пространства частных решений линейного однородного дифференциального уравнения. Множество частных решений линейного однородного дифференциального уравнения образует линейное пространство.
 Док-во. Требуется доказать, что множество частных решений линейного однородного дифференциального уравнения (25) (или, что тоже самое, (21)), т.е. не менее n раз дифференцируемых функций y (x) для которых Ln (y) = 0, является линейным пространством. Для этого достаточно доказать, что если функции y, y 1(x), y 2(x) - частные решения (25), то функции Cy, y 1(x) + y 2(x) - тоже частные решения (25). Действительно, пользуясь свойствами пункта уравнения.
Док-во. Требуется доказать, что множество частных решений линейного однородного дифференциального уравнения (25) (или, что тоже самое, (21)), т.е. не менее n раз дифференцируемых функций y (x) для которых Ln (y) = 0, является линейным пространством. Для этого достаточно доказать, что если функции y, y 1(x), y 2(x) - частные решения (25), то функции Cy, y 1(x) + y 2(x) - тоже частные решения (25). Действительно, пользуясь свойствами пункта уравнения.





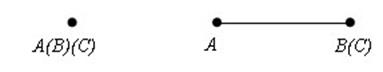 Если две токи из трех или все три точки совпадают, то утверждение теоремы очевидно.
Если две токи из трех или все три точки совпадают, то утверждение теоремы очевидно.  Если все точки различны и лежат на одной прямой, то AB + BC = AC. Отсюда видно, что каждое из трех расстояний не больше суммы двух других.
Если все точки различны и лежат на одной прямой, то AB + BC = AC. Отсюда видно, что каждое из трех расстояний не больше суммы двух других.  Если три точки не лежат на одной прямой докажем, что AC< доказана. Теорема ВС. + AB AC то BC, DC и AD как Так DC. ≤ доказанному По AC. прямую на BD перпендикуляр Опустим>
Если три точки не лежат на одной прямой докажем, что AC< доказана. Теорема ВС. + AB AC то BC, DC и AD как Так DC. ≤ доказанному По AC. прямую на BD перпендикуляр Опустим>

