При побудові формул будемо використовувати в основному такі символи:
1) х, у, z, u, v, w, а також ці букви з індексами - для позначення предметних змінних;
2) а, b, c, d, e або ці ж букви з індексами - для позначення предметних констант;
3) f, g, h або ці ж букви з індексами - для позначення функціональних символів; якщо необхідно відзначити місткість (кількість аргументів) функції, то використовуватимемо верхній індекс. Наприклад,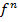 
означатиме n - місний функціональний символ;
4) P, Q, R, S, T або ці ж букви з індексами - для позначення предикатних символів; якщо необхідно вказати місткість предиката, то використовуватимемо верхні індекси, наприклад 
(позначення тримісного предиката);
5)┐, ᴧ, ∨, →, ↔, 
- для позначення знаків логічних операцій;
6) круглі дужки і кома – допоміжні.
Спочатку дамо визначення терма:
1) предметні змінні і предметні константи є термами;
2) якщо 
– терми, а 
– функціональні символи, то 
, 
, 
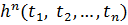– терми;
У логіці висловлень елементарним об’єктом, якому притаманне значення істинності, є атомарне висловлення, яке не можна поділити на компоненти. У логіці предикатів таким елементарним об’єктом, якому притаманне значення істинності, є атомарна формула. Такі формули називають також елементарними. Атомарна формула записується як позначення предиката, за яким в дужках розташовуються аргументи. Кожний аргумент - це терм. Атомарна формула має такий загальний вигляд:
, де 
- предикатний символ, а 
- терми. Зокрема, 
атомарна формула.
Формули логіки предикатів одержують з атомарних за допомогою знаків логічних операцій. Означення:
1. Атомарна формула є формулою логіки предикатів.
2. Якщо α і β - формули логіки предикатів, то (┐α), (α ᴧ β), (α∨β), (α→β), (α↔β) також формули логіки предикатів.
3. Якщо α(x) - формула логіки предикатів, то 
і 
також формули логіки предикатів.
У формули логіки предикатів можуть входити як вільні, так і зв’язані змінні. Формули, які не містять жодної вільної змінної називаються замкненими або реченнями, а ті, що містять вільні предметні змінні, називаються відкритими.
Зазначимо, що при різноманітних перетвореннях формул часто користуються підстановками термів замість вільних змінних. змінних. Наприклад, результатом підстановки у формулу 
терма f(u) замість y 
є формула 
Проте не кожний терм можна підставлят и замість вільної змінної. Наприклад, якщо P(u, v) інтерпретувати як «u = v», то формула 
, де 
, для будь - якого фіксованого у є істинним висловленням. Якщо здійснити підстановку 
, то дістаємо тотожно хибне висловлення 
. Отже, неможна здійснювати підстановку, в результаті якої вільна змінна, замість якої підставляється терм, перетворюється на зв’язану.
Означення. Терм t називається допустимим для підстановки у формулу α(x) замість x (або вільним для змінної в α(x)), якщо жодне вільне входження x в α не знаходиться в області дії ніякого квантора 
y або y, де y – змінна, яка входить в t.
