Понятие об интенсивных переменных
Состояния фаз в равновесной системе.
Пусть имеется равновесная система с произвольным двухмерным множеством компонентов и фаз {к(a)} 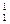 (к=1,…, К), (α=1,…,А), где все фазы однородны и электронейтральны.
(к=1,…, К), (α=1,…,А), где все фазы однородны и электронейтральны.
Выберем для определения состояния каждой фазы α независимые переменные вида Т, р, {n 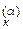 }
} 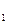 (к=1,…, К), где Т и р имеют интенсивный характер, а {n
(к=1,…, К), где Т и р имеют интенсивный характер, а {n 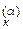 }
} 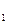 – экстенсивный характер. На этой основе запишем локальные и глобальные уравнения состояния данной фазы, учитывая, что её интенсивные свойства I
– экстенсивный характер. На этой основе запишем локальные и глобальные уравнения состояния данной фазы, учитывая, что её интенсивные свойства I  – однородные функции 0-й степени, а экстенсивные свойства Е
– однородные функции 0-й степени, а экстенсивные свойства Е  –однородные функции 1-й степени относительно аргументов {n
–однородные функции 1-й степени относительно аргументов {n  }
} 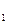 :
:
I  = I
= I  (Т, р, {n
(Т, р, {n  }
} 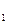 ) = I
) = I  (Т, р, { N
(Т, р, { N  }
} 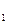 ),
),
Е  = Е
= Е  (Т, р, {n
(Т, р, {n  }
} 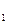 ) = Е
) = Е  (Т, р, { N
(Т, р, { N  }
} 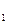 ) ∙ n,
) ∙ n,
где { N  }
} 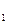 (i =2,…,К) – множество независимых мольных долей компонентов в данной фазе.
(i =2,…,К) – множество независимых мольных долей компонентов в данной фазе.
Новые независимые переменные Т, р, { N  }
} 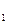 в этих уравнениях имеют интенсивный характер и называются интенсивными переменными состояния фазы α. Очевидно, что они служат аргументами для всех интенсивных свойств I
в этих уравнениях имеют интенсивный характер и называются интенсивными переменными состояния фазы α. Очевидно, что они служат аргументами для всех интенсивных свойств I  (куда входят также все мольные экстенсивные свойства Е
(куда входят также все мольные экстенсивные свойства Е 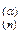 ). Их множество { Т, р, { N
). Их множество { Т, р, { N  }
} 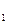 } будем называть частным множеством интенсивных переменных состояния данной фазы.
} будем называть частным множеством интенсивных переменных состояния данной фазы.
Объединение таких множеств по всем фазам α дает общее множество интенсивных переменных состояния фаз в равновесной системе, обозначаемое так:
{ Т, р, { N  }
} 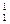 }=
}= 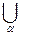 { Т, р, { N
{ Т, р, { N  }
} 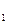 },
},
где { N  }
} 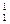 (i =2,…,К), (α=1,…,А) – двухмерное множество независимых мольных долей компонентов во всех фазах.
(i =2,…,К), (α=1,…,А) – двухмерное множество независимых мольных долей компонентов во всех фазах.
Функциональные связи между интенсивными переменными
состояния фаз в равновесной системе и причины их появления.
Суть проблемы сводится к тому, что в равновесной системе интенсивные переменные общего множества { Т, р, { N  }
} 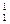 } связаны между собой функционально, поэтому одни из них имеют характер свободныхпеременных (аргументов), а другие – несвободных переменных (функций).
} связаны между собой функционально, поэтому одни из них имеют характер свободныхпеременных (аргументов), а другие – несвободных переменных (функций).
Свободные переменные можно менять произвольно в некоторых физически допустимых интервалах значений с целью перевода системы из одного равновесного состояния в другое без изменения числа фаз и числа компонентов. При этом несвободные переменные принимают вполне определенные значения, обусловленные их функциональными зависимостями от свободных переменных. Достигаемая таким путем последовательная смена равновесных состояний системы называется смещением равновесий в системе.
Отсюда заключаем, что в случае равновесной системы общее множество интенсивных переменных состояния фаз распадается на два непересекающихся подмножества (класса) по следующей схеме:
{ Т, р, { N  }
} 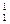 }= {свободные переменные}
}= {свободные переменные}  {несвободные переменные}.
{несвободные переменные}.
(аргументы) (функции)
Перечислим теперь причины возникновения функциональных связей между интенсивными переменными состояния фаз в равновесной системе:
1) Условие массового равновесия между фазами α:
μ  (Т, р, { N
(Т, р, { N  }
} 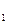 ) =…= μ
) =…= μ  (Т, р, { N
(Т, р, { N  }
} 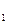 ) = μ
) = μ  (Т, р, { N
(Т, р, { N  }
} 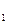 ),
),
(к =1,…, К)
2) Условие химического равновесия между компонентами k:

 μ
μ  (Т, р, { N
(Т, р, { N  }
} 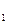 ) d
) d  n
n  = 0,
= 0,
3) Особые условия равновесия, действующие лишь в некоторых конкретных системах, например, условие равенства мольных долей каждого компонента в двух сосуществующих фазах ε и λ:
N  = N
= N  (к =1,…, К)
(к =1,…, К)
 Переход к независимым мольным долям
Переход к независимым мольным долям
N 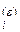 = N
= N  (i =2,…,К).
(i =2,…,К).
Понятие о вариантности равновесной системы.
Пусть а – число интенсивных переменных состояния фаз в равновесной системе, в – число функциональных уравнений связи между этими переменными. Тогда разность между а и в, обозначаемая через
ω = а – в
дает число свободных переменных, называемое вариантностью равновесной системы (по старой терминологии, числом степеней свободы равновесной системы).
Из этого определения ω следует, что число несвободных переменных совпадает с числом в, поскольку а = ω+ в.
Уравнение Гиббса для расчета вариантности






