Коэффициент корреляции равен r=0,90.
Значение коэффициента корреляции говорит о высокой степени линейной корреляции величины у и х.
Стандартная ошибка определения коэффициента парной корреляции равна 
.
Достоверность расчёта коэффициента корреляции высока:
.
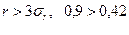Доверительный интервал коэффициента корреляции находится в пределах:
.
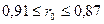Корреляционное отношение равно:
.
Стандартная ошибка его определения равна .
Корреляционное отношение не даёт дополнительной информации, т.к. связь между у и х тесна и близка к линейной.
Коэффициент детерминации В=0,81 показывает, что примерно 
изменений величины у вызвано изменением величины х.
Стандартное отклонение у от поверхности регрессии составляет Sy=1,88, т.е. находится в пределах от 5,5 до 8,10% от значений величины 
:
и 
.
Экономические характеристики производственной функции 
Дополнительный продукт фактора:
, т.е. 
.
Средняя производительность:
;
при х1=30;
;
при х=52
.
Коэффициент эластичности:
;
при х=50 коэффициент эластичности равен
,
т.е. при изменении (х) на 1% величина (у) изменится на 0,76%.
Демонстрационная задача № 3
Используя данные о фактической величине потерь на холостые повороты и заезды тракторных агрегатов при выполнении полевых работ в зависимости от длины гона, определить расчетные значения величины потерь, величину корреляционного отношения, его ошибку, критерий достоверности и доверительные границы корреляционного отношения.
Таблица 7
Исходные данные
| № п/п (j) | Фактическая величина потерь, % (yj) | Длина гона, км (xj) |
| 16.8 | 0.4 | |
| 10.8 | 0.7 | |
| 6.2 | 1.0 | |
| 6.0 | 1.3 | |
| 4.0 | 1.6 | |
| 3.8 | 1.9 | |
| 3.1 | 2.2 | |
| 16.0 | 0.5 | |
| 13.8 | 0.6 | |
| 12.1 | 0.7 | |
| 10.0 | 0.8 | |
| 9.0 | 0.9 | |
| 5.8 | 1.0 | |
| 8.1 | 1.1 |
Решение
Для определения зависимости между значением фактической величины потерь на холостые повороты и заезды тракторных агрегатов при выполнении полевых работ и длиной гона построим график в двухмерной системе координат (x,y), где у – величины потерь на холостые повороты (%) и заезды, х – длина гона (км) (рис. 3).
Рисунок свидетельствует о наличии гиперболической зависимости. Уравнение гиперболы имеет вид y=a0+a1/x.
Для расчета параметров «a0» и «a1» решается система уравнений:
 |
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8
Рис. 3. Графическое представление зависимости между значением фактической величины потерь на холостые повороты и заезды тракторных агрегатов и длиной гона. Точками показаны результаты наблюдений
;
;
.
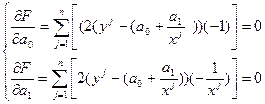Промежуточные вычисления, необходимые для решения системы нормальных уравнений, приведены в табл. 8.
Таблица 8
Расчет коэффициентов системы нормальных уравнений
(случай гиперболической регрессии)
| № п/п (j) | Фактическая величина потерь, % (yj) | Длина гона, км (xj) | 1/хj | 1/(хj)2 | yj/xj | Расчетная величина потерь, %, ŷ j |
| 16.8 | 0.4 | 2.5 | 6.25 | 42.0 | 19.32 | |
| 10.8 | 0.7 | 1.429 | 2.04 | 15.429 | 11.35 | |
| 6.2 | 1.0 | 1.0 | 1.0 | 6.2 | 8.17 | |
| 6.0 | 1.3 | 0.769 | 0.59 | 4.615 | 6.45 | |
| 4.0 | 1.6 | 0.625 | 0.39 | 2.5 | 5.38 | |
| 3.8 | 1.9 | 0.526 | 0.28 | 2.0 | 4.64 | |
| 3.1 | 2.2 | 0.455 | 0.21 | 1.409 | 4.11 | |
| 16.0 | 0.5 | 2.0 | 4.0 | 32.0 | 15.60 | |
| 13.8 | 0.6 | 1.666 | 2.78 | 23.0 | 13.12 | |
| 12.1 | 0.7 | 1.429 | 2.04 | 18.714 | 11.35 | |
| 10.0 | 0.8 | 1.25 | 1.56 | 16.25 | 10.02 | |
| 9.0 | 0.9 | 1.111 | 1.23 | 11.444 | 8.99 | |
| 5.8 | 1.0 | 1.0 | 1.0 | 9.2 | 8.17 | |
| 8.1 | 1.1 | 0.909 | 0.83 | 7.364 | 7.49 | |
| S | 125,5 | 16.669 | 24.20 | 192.125 |
Используя результаты расчёта табл. 8 запишем систему нормальных уравнений в виде:
; 
;
; 
;
; 
.
Сглаженная зависимость потерь на холостые повороты и заезды тракторных агрегатов от длины гона имеет вид:
y=0.726+7.439/x.
Поскольку зависимость между длиной гона и величиной потерь на холостые повороты и заезды тракторных агрегатов носит нелинейный характер, тесноту нелинейных связей можно характеризовать выборочным корреляционным отношением:
О степени линейной корреляции можно судить по значению ryx.
.
Для расчета величин (y-ŷ)2, (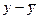
) 2 составим таблицу 9.
Таблица 9
Таблица для расчета корреляционного отношения
| № п/п (j) | Фактическая величина потерь, % (yj) | 
| Расчетная величина потерь, %, yj |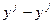 
| 
|
| 16.8 | 51,84 | 19.32 | -2,52 | 6,35 | |
| 10.8 | 1,44 | 11.35 | -0,55 | 0,30 | |
| 6.2 | 11,56 | 8.17 | -1,97 | 3,88 | |
| 6.0 | 12,96 | 6.45 | -0,45 | 0,20 | |
| 4.0 | 31,36 | 5.38 | -1,38 | 1,90 | |
| 3.8 | 33,64 | 4.64 | -0,84 | 0,71 | |
| 3.1 | 42,25 | 4.11 | -1,01 | 1,02 | |
| 16.0 | 40,96 | 15.60 | 0,40 | 0,16 | |
| 13.8 | 17,64 | 13.12 | 0,68 | 0,46 | |
| 12.1 | 12,25 | 11.35 | 1,75 | 3,06 | |
| 10.0 | 11,56 | 10.02 | 2,98 | 8,88 | |
| 9.0 | 0,49 | 8.99 | 1,31 | 1,72 | |
| 5.8 | 0,16 | 8.17 | 1,03 | 1,06 | |
| 8.1 | 2,25 | 7.49 | 0,61 | 0,37 | |
| S | 134.2 | 270,36 | 134,16 | 30,07 | |
| ∑/ п |
|
Подставляя найденные значения величин в формулу, получим:
.
Стандартная (среднеквадратическая) ошибка определения коэффициента корреляции и корреляционного отношения может быть оценена по формулам:
при 
; 
=______
.
где N – объем выборки (случай, когда N<30);
K – число факторов.
Достоверность расчёта корреляционного отношения высока.
Очень большое значение выборочного корреляционного отношения и малая погрешность его определения говорят об адекватности принятой регрессионной зависимости реальной статистической картине, о верности выбранной гиперболической зависимости между величинами у и х.
Степень влияния фактора на результат, определяется значением коэффициента детерминации.
Коэффициент детерминации вычисляется по формуле:
; где Дрег и Дост – дисперсии отклонений сглаженных значений ŷ j от среднего наблюдаемого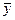 
и отклонений наблюдаемых величин 
от сглаженного 
.
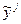Коэффициент детерминации равный В=0,. 89 характеризует, что ….% изменений величины у вызвано изменением величины х, а (1-В) 
….% влиянием неучтённых факторов.
Несмещённая выборочная оценка для дисперсии отклонений случайной величины у от поверхности регрессии вычислим по формуле:
Стандартное отклонение величины у от линии регрессии составляет…., т.е. находится в пределах 
% от значений величины .
.
Задания для лабораторных и самостоятельных работ.
Задача № 1
Используя фактические данные (табл. 11) определить сглаженную зависимость площади лесных полос от крутизны склона в районе развитой эрозии почв. Рассчитать показатели, характеризующие тесноту связи между площадью лесных полос и крутизной склона, адекватность выбранной регрессионной зависимости, степень влияния изменения значений фактора на изменение величины результирующего показателя. Решить задачу в ручную.
Таблица 10
Исходные данные к задаче
| № п/п (j) | Площадь лесополос,%, (yj) | Крутизна склона в градусах |
| 2.2 | 0.3-.0.5 | |
| 2.5 | 0.5-.1.0 | |
| 2.9 | 1.-.2.2 | |
| 3.1 | 2.1-.2.5 | |
| 3.3 | 2.5-.3.0 | |
| 4.0 | 3.0-.3.5 | |
| 4.7 | 3.5-.4.0 | |
| 5.0 | 4.0-4.5 | |
| 5.2 | 4.5-5.0 | |
| 5.5 | 5.0-5.7 | |
| 5.8 | 5.7-6.0 | |
| 6.0 | 6.0-6.5 | |
| 6.2 | 6.5-7.0 | |
| 6.7 | 7.0-7.8 |
Задача № 2
Имеются данные о динамике урожайности ячменя в хозяйстве за ряд лет с 1982 по 1994гг. представлены в табл. 12 (ц/га).
Таблица 11
Исходные данные к задаче (Вариант 1)
| Годы (j) | Порядковый номер года, (хj) | Фактическая урожайность, ц/га, (у) |
Таблица 12
Исходные данные к задаче (Вариант 2)
| Годы (j) | Порядковый номер года, (хj) | Фактическая урожайность, ц/га, (у) |
По заданной статистической информации установить функциональную зависимость урожайности ячменя от времени.
Рассчитать планируемую урожайность ячменя в 2010 году.
Рассчитать показатели, характеризующие тесноту связи между урожайностью ячменя и годами, адекватность выбранной регрессионной зависимости, степень влияния изменения значений фактора на изменение величины результирующего показателя. Решить задачу в ручную.
Задача № 3
По заданной статистической информации установить функциональную зависимость валового внутреннего продукта (дохода) от объема личных потребительских расходов (потребление) за ряд лет с 1983 по 1992 г.г. (млрд. долларов в ценах 1987 г.). Приведем данные в виде таблицы 15 по валовому внутреннему продукту (ВВП - доходу) и объему личных потребительских расходов (потребление) в США, в млрд. долларов в ценах 1987 г.
Таблица 13
Исходные данные
| Год | ||||||||||||
| Доход | ||||||||||||
| Потребление |
Представим статистическую информацию в виде, пригодном для решения задачи на ПЭВП (табл. 16)
Таблица 14
Исходные данные к задаче
| j | yj | xj |
| Годы | Доход | Потребление |
Задача № 4
При составлении задания на проектирование необходимо установить планируемую урожайность сельскохозяйственных культур на расчетный 2010 год. По данным годовых отчетов сельскохозяйственных предприятий имеется следующая фактическая урожайность (таблица 17).
Таблица 15
Исходные данные к задаче
| № п/п | Годы (j) | Фактическая урожайность сельскохозяйственных культур, ц/га | ||||||||
| ВарI | ВарII | ВарIII | ВарIV | ВарV | ВарVI | |||||
| Зерновые | Сахарная | Кукуруза | Мн. травы | Гречиха | Кукуруза | |||||
| (хj) | свекла | (зерно) | (сено) | (силос) | ||||||
| (yj) | (yj) | (yj) | (yj) | (yj) | (yj) | |||||
| 12.9 | 32.8 | 6.8 | ||||||||
| 16.0 | 28.7 | 10.4 | ||||||||
| 14.1 | 33.0 | 9.0 | ||||||||
| 14.8 | 37.4 | 11.5 | ||||||||
| 15.5 | 34.6 | 11.0 | ||||||||
| 14.4 | 25.7 | 12.4 | ||||||||
| 17.5 | 27.7 | 12.0 | ||||||||
| 15.6 | 30.2 | 10.5 | ||||||||
| 16.3 | 31.3 | 12.2 | ||||||||
| 17.0 | 34.8 | 10.8 | ||||||||
| 17.7 | 26.2 | 13.0 | ||||||||
| 20.8 | 28.8 | 12.4 | ||||||||
| 18.9 | 25.7 | 13.5 | ||||||||
| 19.6 | 27.3 | 71.2 | ||||||||
| 20.3 | 27.7 | 14.8 | ||||||||
По заданной статистической информации определить функциональную зависимость урожайности сельскохозяйственной культуры во времени.
Провести оценку производственной функции с использованием методов корреляционно-регрессионного анализа.
Задачу решить на ПЭВМ.
Задача № 5
По заданной статистической информации установить регрессионную зависимость урожайности зерновых культур в зависимости от дозы вносимых удобрений. Рассчитать показатели, характеризующие тесноту связи между урожайностью культур и дозой вносимых удобрений, адекватность модели, определить как изменяется урожайность культуры от изменений дозы вносимых удобрений. Решить задачу на ПЭВМ.
Таблица 16
Исходные данные к задаче
| № | Урожайность сельскохозяйственных культур, ц/га | Доза удобрен. | |||||
| уч-в (j) | оз. пшн. (yj) | оз. рожь (yj) | овес (yj) | ячмень (yj) | гречиха (yj) | зернобобовые (yj) | услов. туков (хj) |
| 28.0 | 12.2 | 24.5 | 30.5 | 24.5 | 14.3 | ||
| 28.4 | 14.5 | 21.0 | 30.8 | 21.0 | 16.3 | ||
| 32.5 | 13.0 | 21.3 | 31.1 | 21.3 | 15.1 | ||
| 29.9 | 12.6 | 27.0 | 34.6 | 27.0 | 15.6 | ||
| 28.9 | 15.56 | 28.1 | 38.0 | 28.1 | 17.2 | ||
| 35.0 | 17.0 | 31.0 | 39.4 | 31.0 | 19.5 | ||
| 35.7 | 16.7 | 34.2 | 38.5 | 34.2 | 18.3 | ||
| 36.5 | 17.8 | 30.5 | 41.78 | 30.5 | 18.7 | ||
| 37.7 | 19.0 | 29.3 | 40.6 | 29.3 | 21.1 | ||
| 34.8 | 20.0 | 35.0 | 39.0 | 35.0 | 22.0 | ||
Задача № 6
Определить сглаженную зависимость урожайности зерновых культур от балла качественной оценки земли. Статистическая информация представлены в табл. 19. Рассчитать показатели, характеризующие тесноту связи между урожайностью культур и баллом оценки земель, определить адекватность модели. Задачу решить на ПЭВМ.
Таблица 17
Исходные данные к задаче
| №№ участков | Урожайность зерновых культур, ц/га | Балл качественной оценки земли, (xj) | ||||
| (j) | оз. пшен (y'). | оз. рожь (y') | ячмень (y') | овес (y') | зернобобовые (y') | |
| 23.5 | 22.7 | 25.1 | 19.0 | |||
| 23.7 | 24.1 | 26.1 | 17.3 | |||
| 24.0 | 23.5 | 24.3 | 18.9 | |||
| 26.7 | 26.7 | 25.1 | 16.7 | |||
| 24.3 | 20.9 | 22.1 | 19.1 | |||
| 28.8 | 28.6 | 29.0 | 13.7 | |||
| 33.5 | 25.4 | 30.0 | 26.9 | |||
| 27.6 | 24.5 | 27.6 | 13.4 | |||
| 23.4 | 22.5 | 25.7 | 13.5 | |||
| 29.4 | 26.1 | 29.9 | 18.6 | |||
| 30.5 | 38.0 | 31.0 | 19.7 | |||
| 39.0 | 29.6 | 32.0 | 20.0 |
Задача № 7
Найти зависимость потерь y (%) времени смены на холостые повороты и заезды комбайна СК-6 “Колос” при прямом комбайнировании на уборке зерновых колосовых от длины x (км) гона по исходным данным, представленным в табл. 20. Провести третий этап решения задачи- верификацию (проверку адекватности модели) вручную. Вычислить коэффициент корреляции, корреляционное отношение, коэффициент детерминации.
Таблица 18
Исходные данные к задаче
| № п/п | x, км | y, % | № п/п | x, км | y, % |
| 0,15 | 39,2 | 0,75 | 10,0 | ||
| 0,25 | 23,0 | 1,00 | 8,0 | ||
| 0,35 | 20,0 | 1,25 | 7,0 | ||
| 0,40 | 17,0 | 1,50 | 6,0 | ||
| 0,50 | 13,8 | 1,75 | 5,2 | ||
| 0,60 | 12,5 | 2,00 | 4,9 |
Решение
Для определения зависимости потерь времени смены на холостые повороты и заезды от длины гона по исходным данным построим график в двухмерной системе координат (x,y), где y (%)- время смены на холостые повороты и заезды, x (км) – длина гона (рис. 4).
Рисунок свидетельствует о наличии гиперболической зависимости. Поэтому выбираем уравнение регрессии вида: 
.
В соответствии с принятым видом уравнения регрессии, коэффициенты a 1 и a 2 регрессии могут быть найдены из решения системы линейных уравнений вида:
.
Промежуточные вычисления, необходимые для приведения системы к конкретному виду, представлены в табл. 19.
 |
0 0,5 1,0 1,5 2,0 x
Рис. 4. Сглаженная зависимость потерь y (%) времени смены на холостые повороты и заезды на уборке зерновых от длины x (км) гона. Точками показаны результаты наблюдений
Таблица 19
Расчет коэффициентов системы нормальных уравнений
(случай гиперболической регрессии)
| № п/п | y | x | 1/x | 1/x2 | y/x | 
|
| 39,2 23,0 20,0 17,0 13,8 12,5 10,0 8,0 7,0 6,0 5,2 4,9 | 0,15 0,25 0,35 0,40 0,50 0,60 0,75 1,00 1,25 1,50 1,75 2,00 | 6,67 4,00 2,86 2,50 2,00 1,67 1,33 1,00 0,80 0,67 0,57 0,50 | 44,44 16,00 8,16 6,25 4.00 2.78 1.78 1.00 0.64 0.44 0.33 0.25 | 261,33 92,00 57,14 42,50 27,60 20,83 13,33 8,00 5,60 4,00 2,97 2,45 | 39,27 24,62 18,34 16,37 13,63 11,79 9,96 8,13 7,03 6,3 5,77 5,38 | |
| S | 166,6 | 10,50 | 24,56 | 537,76 | 86,07 | 166,60 |
С использованием результатов, представленных в последней строке табл. 21, систему нормальных уравнений приведем к виду:
.
Искомое уравнение регрессии имеет вид:
.
Задача № 8
Определить сглаженную зависимость потерь рабочего времени на холостые повороты и заезды при уборке зерновых культур от длины гона. Исходные данные приведены в таблице 22.
Таблица 20
Исходные данные к задаче
| № п/п (j) | Фактическая величина потерь, % (yj) | Длина гона, км (xj) | № п/п (j) | Фактическая величина потерь, % (yj) | Длина гона, км (xj)) |
| Вариант 1 | Вариант 2 | ||||
| 0.3 | 20,0 | ||||
| 0.4 | 10,3 | 1,2 | |||
| 0.5 | 8,0 | 1,7 | |||
| 0.6 | 6,0 | 2,2 | |||
| 0.7 | 5,5 | 2,7 | |||
| 0.8 | 5,4 | 3,0 | |||
| 0.9 | 5,5 | 3,2 | |||
| 1.0 | 18,0 | 0,7 | |||
| 1.1 | 15,8 | 0,8 | |||
| 7.3 | 1.2 | 15,1 | 0,9 | ||
| 6.8 | 1.3 | 17,0 | 1,0 | ||
| 6.4 | 1.4 | 12,3 | 1,1 | ||
| 6.0 | 1.5 | 11,2 | 1,2 | ||
| 5.7 | 1.6 | 10,1 | 1,2 | ||
| 5.4 | 1.7 | 14,5 | 0,4 | ||
| 5.0 | 1.8 | 6,0 | 0,8 | ||
| 4.7 | 1.9 | 4,2 | 1,2 | ||
| 4.5 | 2.0 | 4,5 | 1,6 | ||
| 4.2 | 2.1 | 3,5 | 2,0 | ||
| 4.0 | 2.2 | 3,6 | 1,9 |
Рассчитать коэффициенты для системы нормальных уравнений в случае гиперболической зависимости: 
.
Вид системы нормальных уравнений:
.
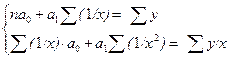Таблица 21
Таблица для расчета параметров
| № п/п (j) | Фактическая величина потерь, %, (yj) | Длина гона, км, (xj) | 1/хj | 1/(хj)2 | yj/хj | Расчетная величина потерь, % ý=f(xj) |
| 0.3 | ||||||
| 0.4 | ||||||
| 0.5 | ||||||
| 0.6 | ||||||
| 0.7 | ||||||
| 0.8 | ||||||
| 0.9 | ||||||
| 1.0 | ||||||
| 1.1 | ||||||
| 7.3 | 1.2 | |||||
| 6.8 | 1.3 | |||||
| 6.4 | 1.4 | |||||
| 6.0 | 1.5 | |||||
| 5.7 | 1.6 | |||||
| 5.4 | 1.7 | |||||
| 5.0 | 1.8 | |||||
| 4.7 | 1.9 | |||||
| 4.5 | 2.0 | |||||
| 4.2 | 2.1 | |||||
| 4.0 | 2.2 | |||||
| S |
Рассчитать:
* показатели, характеризующие тесноту связи между потерями рабочего времени и длиной гона;
* затраты Z на холостые повороты и заезды на пашне, площадью 100 га, используя следующую формулу:
Z = O·S·P· (Y/100), руб,
где O - коэффициент перевода в условную мягкую пахоту. (В расчетах принять равным 5, что характерно для Западно-Сибирского, Центрального и Поволжского районов);
S - нормативная стоимость 1 гектара условной пахоты, руб. (В расчетах принять S = 50 руб);
P - площадь поля, га;
Y - средневзвешенный процент потерь на холостые повороты и заезды на данном поле. (В расчетах принять, что на поле длина гона (x) распределена следующим образом: 20% - x = 0,2 км, 50% - x = 0,8 км, 30% - x = 1,5 км).
Задача № 9
Используя данные о фактической величине потерь на холостые повороты и заезды тракторных агрегатов при выполнении полевых работ в зависимости от длины гона табл. 24, определить расчетные значения величины потерь, коэффициент корреляции, величину корреляционного отношения, ошибку его определения, доверительный интервал корреляционного отношения, коэффициент детерминации. Определить возможные экономические характеристики. Решить задачу на ПЭВМ.
Таблица 22
Исходные данные к задаче
| № п/п (j) | Фактическая величина потерь, %, (yj) | Длина гона, км, (xj) | Фактическая величина потерь, %, (yj) | Длина гона, км, (xj) | Фактическая величина потерь, %, (yj) | Длина гона, км, (xj) |
| Вариант 1 | Вариант 2 | Вариант 3 | ||||
| 19.5 | 0.4 | 15.0 | 0.6 | 18.0 | 0.5 | |
| 19.5 | 0.5 | 12.3 | 0.8 | 8.3 | 1.0 | |
| 14.0 | 0.6 | 9.5 | 1.0 | 6.0 | 1.5 | |
| 12.5 | 0.8 | 7.4 | 1.5 | 4.0 | 2.0 | |
| 12.0 | 1.0 | 5.0 | 2.0 | 3.5 | 2.5 | |
| 7.0 | 1.5 | 4.0 | 2.5 | 3.4 | 2.8 | |
| 7.0 | 2.0 | 3.7 | 3.0 | 3.5 | 3.0 | |
| 15.7 | 0.3 | 16.8 | 0.4 | 16.0 | 0.5 | |
| 10.0 | 0.5 | 10.8 | 0.7 | 13.8 | 0.6 | |
| 9.4 | 0.7 | 6.2 | 1.0 | 13.1 | 0.7 | |
| 6.5 | 0.9 | 6.0 | 1.3 | 13.0 | 0.8 | |
| 6.3 | 1.2 | 4.0 | 1.6 | 10.3 | 0.9 | |
| 4.4 | 1.8 | 3.8 | 1.9 | 9.2 | 1.0 | |
| 3.9 | 2.0 | 3.1 | 2.2 | 8.1 | 1.1 | |
| 15.0 | 0.4 | 12.0 | 0.8 | 12.5 | 0.2 | |
| 12.2 | 0.6 | 8.5 | 1.1 | 4.0 | 0.6 | |
| 8.0 | 0.8 | 6.0 | 1.4 | 2.2 | 1.0 | |
| 7.6 | 1.0 | 5.9 | 1.7 | 2.5 | 1.4 | |
| 5.8 | 1.2 | 5.7 | 2.0 | 1.5 | 1.8 | |
| 5.0 | 1.4 | 4.0 | 2.3 | 1.0 | 2.2 | |
| 4.1 | 1.6 | 3.7 | 2.6 | 0.9 | 2.6 | |
| 23.0 | 0.2 | 17.0 | 0.2 | 15.1 | 0.51 | |
| 9.8 | 0.8 | 11.8 | 0.4 | 7.0 | 1.0 | |
| 6.2 | 1.0 | 8.8 | 0.5 | 6.2 | 1.6 | |
| 5.6 | 1.5 | 6.5 | 0.6 | 6.0 | 2.0 | |
| 3.4 | 2.0 | 5.5 | 0.8 | 5.2 | 2.4 | |
| 3.3 | 2.5 | 4.0 | 1.0 | 4.3 | 2.5 | |
| 1.7 | 3.0 | 2.5 | 1.2 | 3.0 | 2.6 |
Задача № 10
По заданной статистической информации табл. 25 установить функциональную зависимость стоимости валовой продукции от производственных факторов для сельскохозяйственных организаций административного района.
Решить задачу на ПЭВМ.
Провести оценку модели.
Рассчитать экономические показатели для полученной зависимости.
Таблица 23
Исходные данные
| № предприятия | Стоимость валовой продукции, руб/га | Балл бонитета пашни | Среднее расс-тояние до пашни, км | Средний размер контура, га | Доходы полеводства, руб/га | Трудоспособные, чел га |
| j | (yj) | (x1j) | (x2j) | (x3j) | (x4j) | (x5j) |
| 6.5 | 11.3 | 0.32 | ||||
| 5.9 | 12.4 | 0.39 | ||||
| 12.5 | 10.0 | 0.15 | ||||
| 19.8 | 4.2 | 0.20 | ||||
| 8.3 | 4.8 | 0.39 | ||||
| 7.6 | 6.6 | 0.38 | ||||
| 11.1 | 40.5 | 0.40 | ||||
| 5.2 | 5.4 | 0.22 | ||||
| 7.7 | 22.3 | 0.32 | ||||
| 3.3 | 12.5 | 0.19 | ||||
| 6.9 | 25.0 | 0.54 | ||||
| 10.5 | 10.1 | 0.37 | ||||
| 6.5 | 8.4 | 0.29 | ||||
| 6.1 | 29.2 | 0.43 | ||||
| 10.7 | 2.9 | 0.11 |
Задача № 11
По заданной статистической информации табл. 26 установить функциональную зависимость стоимости валовой продукции от производственных факторов для сельскохозяйственных организаций административного района.
Решить задачу на ПЭВМ.
Провести оценку модели.
Рассчитать экономические показатели для полученной зависимости.
Таблица 24
Исходные данные
| № предприятия | Стоимость валовой продукции, руб/га | Внесение мине-ральных удобрений, ц усл.тук./га | Средний раз-мер севооборота, га | Удельный вес мелиорированной пашни, % | Внесение навоза, т/га | Использование сортовых семян, % |
| j | (yj) | (x6j) | (x7j) | (x8j) | (x9j) | (x10j) |
| 3.1 | 3.4 | |||||
| 3.4 | 6.2 | |||||
| 3.0 | 4.5 | |||||
| 2.9 | 2.2 | |||||
| 2.5 | 6.8 | |||||
| 3.0 | 5.8 | |||||
| 2.7 | 5.4 | |||||
| 2.2 | 3.3 | |||||
| 4.4 | 8.4 | |||||
| 4.0 | 7.6 | |||||
| 4.2 | 8.0 | |||||
| 3.0 | 5.9 | |||||
| 2.1 | 3.3 | |||||
| 3.7 | 7.3 | |||||
| 1.9 | 2.8 |
Задача № 12
По исходным данным, представленным в таблице 27, рассчитать сглаженную зависимость урожайности y (ц/га) кукурузы на зерно от затрат на удобрения (x1) (руб/га) и на семена (x2) (руб/га).
Таблица 25
Исходные данные
| № п/п | Урожайность кукурузы на зерно, ц/га | Затраты на удобрение, руб/га | Затраты на семена, руб/га | № п/п | Урожайность кукурузы на зерно, ц/га | Затраты на удобрение, руб/га | Затраты на семена, руб/га |
| j | yj | x1 | x2 | j | yj | x1 | x2 |
| 34.1 | 4.1 | 2.7 | 34.0 | 4.5 | 4.0 | ||
| 40.0 | 6.2 | 5.4 | 43.2 | 7.0 | 5.2 | ||
| 38.2 | 5.6 | 5.8 | 22.3 | 1.4 | 4.2 | ||
| 42.1 | 6.1 | 5.9 | 42.4 | 7.0 | 7.1 | ||
| 30.0 | 4.3 | 2.4 | 28.1 | 3.1 | 2.7 | ||
| 37.2 | 5.3 | 5.6 | 46.7 | 2.3 | 5.9 |
Допустим, что зависимость имеет форму функции Кобба-Дугласа:
.
Провести оценку производственной функции и рассчитать экономические характеристики. Для сравнения подобрать другую зависимость из класса G производственных функций.
Задача № 13
В одном из почвенно-эрозионных районов Белгородской области выделено 20 хозяйств, находящихся в одинаковых природно-экономических условиях. По данным хозяйствам определены следующие показатели: плотности поголовья коров на 100 га сельскохозяйственных угодий - (y), площади кормовых угодий - (x 1) (% от общей площади сельскохозяйственных угодий), стоимости животноводческих построек - (x 2) (тыс. руб. на 100 га сельскохозяйственных угодий), площади смытых земель - (x 3) (% от общей площади сельскохозяйственных угодий). Определить линейную регрессионную зависимость поголовья коров (y)(головы на 100 га сельскохозяйственных угодий) от факторов (x 1, x 2, x 3);.определить дополнительный продукт фактора (Хi). Провести оценку производственной функции. Рассчитать экономические характеристики.
Таблица 26
Исходные данные к задаче
| № п/п | x 1 | x 2 | x 3 | y | № п/п | x 1 | x 2 | x 3 | y |
| 21,5 | 4,9 | 31,3 | 15,7 | 11,3 | 4,0 | 42,1 | 15,0 | ||
| 10,3 | 16,4 | 25,6 | 23,5 | 14,1 | 15,0 | 8,5 | 16,3 | ||
| 12,6 | 14,8 | 21,0 | 13,5 | 15,6 | 6,0 | 11,0 | 11,3 | ||
| 8,9 | 12,3 | 14,8 | 15,0 | 20,4 | 8,0 | 9,5 | 15,9 | ||
| 20,3 | 4,9 | 17,0 | 10,2 | 27,5 | 9,0 | 11,5 | 18,7 | ||
| 29,0 |
