Подготовка к работе.
1. По указанной литературе изучить:
правила локализации решения,
решение одного уравнения,
решение системы n уравнений.
2. Разработать алгоритмы решения задач из варианта задания.
3. Составить программы решения задач.
Контрольные вопросы
1. Задание функции пользователя.
2. Локализация решений уравнения.
3. Решение нелинейного уравнения с использованием функции fzero.
4. Вывод полученных решений уравнения.
5. Локализация решений системы из двух уравнений.
6. Решение системы из двух уравнений.
7. Вывод полученных решений системы уравнений.
Задание к работе
Задача 1. Решение нелинейного уравнения.
- Создать mat-функцию для функции f1 (х)
function f1=fun1(x1); % Файл fun1.m
f1=1.8*x1^4-sin(10*x1);
end;
- Создать mat-функцию для нахождения корня методом половинного деления;
function pol_d=p_delen(a,b,E); % Файл p_delen.m
L=b-a; % определение диапазона аргумента х
while(L>E) % до тех пор, пока не достигнута точность...
c=(a+b)/2;
if fun1(c)*fun1(a)>0 % если знаки одинаковые
a=c; % то смещаем "левую" часть отрезка к середине"
else % иначе
b=c; % то смещаем "правую" часть отрезка к середине"
end; % конец если
L=b-a;
end; % end of while
pol_d=c; % передача результата в основную программу
- Создать mat-функцию для нахождения корня методом простой итерации;
function iter=prost_it(a,b,E); % Файл prost_it.m
ic=0; % устанавливаем счетчик итераций на нуль
while(fun1(a)*fun1(b)<0) % до тех пор, пока знаки разные,...
if (fun1((a+b)/2)<0) % если середина отрезка отрицательна
a=(a+b)/2; % то смещаем "левую" часть отрезка к середине"
else % иначе
b=(a+b)/2; % то смещаем "правую" часть отрезка к середине"
end; % конец если
ic=ic+1; % увеличиваем счетчик числа итераций
if (ic>100) % если число итераций превышает 100
break; % прекращаем выполнения цикла
end; % конец если
if (abs(a-b)<E) % если достигнута заданная точность
break; % прекращаем выполнение цикла
end; % конец если
end; % end of while
- iter=a; % передача результата в основную программу
- Создать mat-функцию для вывода графика.
function graf=grafi(a,b,n); % Файл grafi.m
dx=(a+b)/n;
for i=1:n % цикл создания массивов для вывода графика функции
x(i)=a+(i-1)*dx; % вычисление массива аргумента
y(i)=fun1(x(i)); % вычисление функции
i=i+1;
end; % конец цикла
plot(x,y) % строим график
grid on
- Создать файл программы. Ввести текст заглавия задачи, как комментарий. Ввести в него аргументы в заданных пределах.
- Вывести y(x)=f1(x) в виде XY графика. По нему определить приближенно корни уравнения у(х)=0. Если корни на графике не просматриваются, то изменить пределы изменения аргумента и повторить операции.
- Для каждого корня найти точное значение, используя функцию fzero.
Формат данной функции: x= fzero(fun, x0, options, P1, P2, …)
- Сформировать строку с результатами и вывести ее в заголовок окна графика.
% Задача 1 Файл uravnen.m
% Решение уравнений с одной переменной
clc
clear
n=30;
a=0.12; % начальное значение аргумента "Слева"
E=10^(-5); % точность нахождения корня
b=2; % начальное значение аргумента "Справа"
iter1=prost_it(a,b,E); % вычисление корня методом простой итерации
pol_d1=p_delen(a,b,E); % вычисление корня методом половинного деления
fz=fzero('fun1',[a,b]); % вычисление корнЯ с испльзованием функции fzero
% вывод результатов
fprintf('\n\tвывод результатов\n\t вычисление корня')
fprintf('\n\t\tметодом простой итерации = %f', iter1)
fprintf('\n\t\tметодом половинного деления = %f',pol_d1)
fprintf('\n\t\tс испльзованием функции fzero = %f',fz)
% вывод гафика функции
grafi(a,b,n);
% Получить строку результатов
Result=strcat('x1=',num2str(iter1),' x2=',num2str(pol_d1),' x3=',num2str(fz));
% Включить его в график в форме заголовка
title(Result)
Варианты заданий
| № п/п | Уравнение | Отрезок | Приближенное значение корня | точность |
| 1. | 3 sin Ö x + 0,35x –3,8 = 0 | [ 2; 3] | 2,2985 | 0,0001 |
| 2. | 0,25x3 + x – 1,2502 = 0 | [ 0; 2] | 1,0001 | 0,0001 |
| 3. | 
| [ 0,4; 1] | 0,7376 | 0,0001 |
| 4. | 
| [ 0; 0,85] | 0,2624 | 0,0001 |
| 5. | 0,1 x2 – x ln x = 0 | [ 1; 2] | 1,1183 | 0,0001 |
| 6. | tg x – 1/3 tg3 x + 1/5 tg5 x – 1/3 = 0 | [ 0; 0,8] | 0,3333 | 0,0001 |
| 7. | 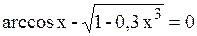
| [ 0; 1] | 0,5629 | 0,0001 |
| 8. | 3 x –4 ln x –5 = 0 | [ 2; 4] | 3,2300 | 0,0001 |
| 9. | cos 2/x – 2 sin 1/x + 1/x = 0 | [ 1; 2] | 1,8756 | 0,0001 |
| 10. | 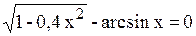
| [ 0; 1] | 0,7672 | 0,0001 |
| 11. | ex – e-x – 2 = 0 | [ 0; 1] | 0,8814 | 0,0001 |
| 12. | sin (ln x) – cos (ln x) + 2 ln x = 0 | [ 1; 3] | 1,3749 | 0,0001 |
| 13. | x – 2 + sin 1/x = 0 | [ 1,2; 2] | 1,3077 | 0,0001 |
| 14. | ex + ln x – 10x = 0 | [ 3; 4] | 3,5265 | 0,0001 |
| 15. | 
| [ 1; 2] | 1,0804 | 0,0001 |
| 16. | 1 – x + sin x – ln (1 + x) = 0 | [ 0; 1,5] | 1,1474 | 0,0001 |
| 17. | 3 x – 14 + ex – e-x = 0 | [ 1; 3] | 2,0692 | 0,0001 |
| 18. | 
| [ 0; 1] | 0,5768 | 0,0001 |
| 19. | x + cos (x0,52 +2) = 0 | [ 0,5; 1] | 0,9892 | 0,0001 |
| 20. | 3 ln(2 x) +6 ln x – 5 = 0 | [ 1; 3] | 1,8832 | 0,0001 |
| 21. | sin x2 + cos x2 - 10 x = 0 | [ 0; 1] | 0,1010 | 0,0001 |
| 22. | x2 – ln(1 + x) – 3 = 0 | [ 2; 3] | 2,0267 | 0,0001 |
| 23. | 2x sin x – cos x = 0 | [ 0,4; 1] | 0,6533 | 0,0001 |
| 24. | 
| [ -1; 0] | -0,2877 | 0,0001 |
| 25. | ln x – x + 1,8 = 0 | [ 2; 3] | 2,8459 | 0,0001 |
| 26. | x tg x – 1/3 = 0 | [ 0,2; 1] | 0,5472 | 0,0001 |
| 27. | tg x/2 – ctg x/2 + x = 0 | [ 1; 2] | 1,0769 | 0,0001 |
| 28. | 0,4 + arctgÖ x – x = 0 | [ 1; 2] | 1,2388 | 0,0001 |
| 29. | 
| [ 0; 1] | 0,4538 | 0,0001 |
| 30. | 0,6 * 3x –2,3 x –3 = 0 | [ 2; 3] | 2,4200 | 0,0001 |
Лабораторная работа № 6






