I. Tension and compression
I. Longitudinal[19] Strain. Stress. Hooke’s Law
Take a prismatic rod of constant cross-sectional area A m2. Mark two thin lines mm apart on its surface using a sharp needle. Now apply two equal and opposite forces, each of P kN, at the ends of the rod so that these forces will act precisely along the axis of the rod. The rod, being in equilibrium under the action of the tensile forces, will elongate in the longitudinal direction and its transverse dimensions will somewhat reduce.
We shall assume that all plane sections normal to the axis of the rod remain plane and normal to its axis after deformation. This hypothesis is known as the hypothesis of plane sections. It is supported by experimental evidence for sections sufficiently far removed from the point of application of the force P, by accepting this hypothesis it is assumed that all longitudinal elements of the rod are stretched in the same manner.
By measuring carefully the distance between the two lines marked on the surface, we find it increased and equal to 
mm. The elongation of the rod in the portion 
is 
.
This increment of the length of the rod is called the total or absolute elongation in tension; in the case of compression it is called the total or absolute contraction. In the latter case the quantity 
has a negative sign.
The absolute elongation depends obviously on the original length of the rod. Therefore, a more convenient measure of deformation is the elongation per unit of original length of the rod. The ratio
,
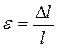is termed the longitudinal strain or the unit elongation. The unit elongation has no dimension; it is a pure number and is often expressed as a percentage of the original length
.
To determine the stress at a transverse section, i. e., at a section perpendicular to the axis of the rod, we apply the general method accepted in strength of materials.
Imagine the rod cut into two parts by a transverse section and the right-hand part removed. To hold the remaining left-hand part in equilibrium, we apply, in the plane of the section, internal elastic forces normal to the plane of the section. These forces replace the action exerted by the removed right-hand part on the left-hand part of the rod. The resultant elastic force will act along the axis of the rod and will be equal to P kN. Accepting the hypothesis of plane sections, we thereby assume that in tension the elastic forces are uniformly distributed over the whole section, therefore, the stress at any point in the cross section is given by the formula
kN/m2.
This stress will be normal since it acts, like the force P, perpendicular to the plane of the cross section. If the force P is measured in kilometers-force and the area A in square meters (centimeters), then the stress will have the dimension kN/m2 (kN/cm2).
In the case of compression the stress is calculated by the same formula, since only the direction of the forces is reversed here.
The magnitude of the stress in tension or compression is independent of the choice of section along the length of the rod. At any cross section the distribution of elastic forces is assumed to be uniform, and only at sections near the point of application of the external force uniform stress distribution is not to be expected. The determination of stresses at such locations is a difficult problem which is beyond the scope of a course in strength of materials.
The loads and the deformations produced in a rod are closely related. This relationship between load and deformation was first formulated by R. Hooke in 1678. According to Hooke’s law deformation is proportional to load. This is one of the fundamental laws in strength of materials. For a rod in tension or compression, Hooke’s law expresses direct proportionality between stress and strain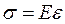 
.
This proportionality is violated when the stress exceeds a certain limit called the proportional limit. The proportional limit for materials is established by experiment.
The factor E appearing in formula is known as the modulus of elasticity of the first kind or Young’s modulus, after the name of the physicist who introduced it into the science. From formula it is seen that the dimension of the modulus of elasticity E is the same as that of stress since 
is a dimensionless[20] quantity, i. e., E is expressed in kN/m2 (kN/cm2). For one and the same stress, the strain will be smaller for a material for which E is larger. Consequently the modulus of elasticity characterizes the stiffness[21] of the material, i. e., its ability to resist deformation, a fact which follows from, formula
.
The magnitude of the modulus of elasticity of materials is established experimentally. In table 1 are given average values of E for some materials at room temperature.
Table 1
Module of Elasticity
| Material | Steel | Cast iron | Bronze | Titanium | Aluminum | Copper | Wood |
| E, MPa | 
| 
| 
| 
| 
| 
| 
|
For materials which do not obey Hooke’s law, such as stone, cement, leather, cast iron, etc., a power relation is used: 
. The exponent m, which is sometimes close to unity, is chosen experimentally. Formula, which expresses Hooke’s law, may be written in an alternate form substituting the appropriate expressions for 
and 
and 
;
we then obtain 
.
From this formula it follows that the elongation (contraction) of the rod is directly proportional to the tensile (compressive) force and the length of the rod, and inversely proportional to the cross-sectional[22] area and the modulus of elasticity of the material. Sometimes the module in compression and tension are not equal (cast iron).
The product in the denominator of formula, i. e., 
is termed the stiffness in tension (compression). The greater the stiffness of the rod, the smaller is the deformation for one and the same length of the rod. The stiffness characterizes simultaneously the physical properties of the material and the geometric dimensions of the section. Formula for stress and Hooke’s law or are fundamental formulas in design for tension and compression.
Example
A steel bolt 160 mm long undergoes an elongation 
= 0,12 mm during tightening. The modulus of elasticity of the material is E = 
MPa. Determine the stress in the bolt.
Solution. The unit elongation is 
.
The stress in the bolt is determined from formula
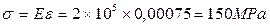
II. Lateral Strain[23] in Tension and Compression
Experiments show that even if a rod undergoes very small deformations in the longitudinal direction its lateral dimensions change. An elongation in the longitudinal direction produces a contraction in the transverse direction and conversely the shortening in the longitudinal direction is accompanied by a lateral expansion. Consequently, a body under tension lengthens and becomes thinner and under compression it shortens and becomes thicker. Lateral strains in tension or compression are proportional to longitudinal strains. If the longitudinal strain is denoted by 
(longitudinal compressive strain) and the lateral strain by 
(lateral tensile strain), then, as is found from experiments, is only a fraction of , i. e.
.
The factor 
is known as Poisson’s ratio.
Poisson’s ratio in tension is defined as and in compression
.
Poisson thought that the ratio 
was the same and equal to 0,25 for all materials. However, subsequent experiments showed that Poisson’s ratio is different for different materials, ranging from 0 to 0,5. Average numerical values of this ratio for some materials are given in table 2. In design practice is taken as 0,3 for steel, beyond the elastic limit increases to 0,5.
Table 2
Poisson’s Ratio for Some Materials
| Material |
| Material |
|
| Cork | Copper | 0,34 | |
| Carbon steel | 0,24 to 0,28 | Bronze | 0,35 |
| Chrome-nickel steels | 0,25 to 0,30 | Rubber | 0,47 |
| Aluminium | 0,26 to 0,36 | Paraffine wax | 0,50 |
Using this ratio, it is possible to determine the change in volume of a rod under tension or compression. Let us first solve this problem in the general form. The volume of a rod of square cross section before extension is
.
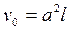After extension each unit of the original length becomes equal to (1+ ), consequently, the new length of the rod becomes equal to 
(1+ 
). The unit of length in the transverse direction shortens and becomes equal to (1–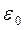 
) or (1– 
). There fore, the cross-sectional area after extension is 
.
The volume of the rod after extension is
.
Neglecting terms containing the factors 
and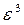 
as small quantities of higher order, we obtain
.
III. Experimental Study of Materials in Tension
The design of structures calls for a knowledge of the properties of materials of which these structures are made. The mechanical properties of materials are revealed by testing them under load.
The test most commonly used is a tension test. The reason for this is that the mechanical characteristics obtained from a tension test make it possible in many cases to predict sufficiently accurately the behaviour of the material under other types of deformation, such as compression, shear,[24] torsion and bending. Besides, a tension test is easiest to perform. Materials which have to withstand primarily compressive loads (stone, concrete, etc.) are tested in compression as well.
Tension tests are carried out on special specimens of materials in specially designed tension testing machines. Specimens are usually of circular section, less frequently of rectangular section. At the ends of a specimen there are heads of heavier section. The heads are inserted into special grips of the testing machine. The transition from the specimen head to the middle (gauge) length is made smooth, in the form of a cone in circular specimens and a fillet in flat specimens. Uniform extension of a specimen occurs over a distance where the specimen section is constant; therefore elongations are measured only over this distance, called the gauge length.[25] The gauge length of the specimen is designated as L.
As experiments show, only geometrically similar specimens of the same material give identical results. Consequently, in comparing mechanical qualities of different materials the absolute dimensions of specimens may by different provided that the law of geometric similarity is maintained.
In the case of brittle materials comparison is made by testing specimens of the same dimensions.
The shapes and dimensions of specimens are standardized, if however, for some reason or other «normal» specimens cannot be prepared, comparable results may be obtained on specimens of circular or rectangular cross section similar to normal ones with the ratio 
, where 
is the gauge length of the specimen and A its cross-sectional area. This value of the ratio 
for a circular specimen is obtained when =10.
In order that a tensile force acts precisely along the specimen axis, the gripping devices of the machine should be built with self-centering spherical seats.
Tension testing machines subject a specimen to a load increasing gradually from zero to a value causing fracture, and provide the so-called static loading. The load is measured by load-measuring instruments (dynamometers).
Tension testing machines vary in construction, shows a schematic diagram of a machine widely used in materials testing laboratories. The heads A of a test specimen are held in the grips of the machine. The lower grip remains stationary during testing. It is raised or lowered only when the specimen is being mounted. The raising or lowering of the lower grip is affected by means of a screw turning the handle. The tensile force is produced by gradually pumping oil into a cylinder mounted on the machine frame. Piston moves up and lifts the upper grip through a system of pin-connected rods. Since the lower grip remains stationary during testing and the upper grip moves up, the specimen is stretched.
Tension testing machines are usually provided with recording instruments which trace a curve showing the relation between the tensile load and the resulting elongation of the specimen. As mentioned, direct measurement of deformations is made with special instruments – strain gauges.
IV. Tension Test Diagram and It’s Characteristic Points
The behaviour of materials in tension[26] is best understood from a consideration of a curve called a tension test diagram, which represents the stress-strain relation in tension. It is usually obtained from a diagram in the coordinates: tensile force P and absolute elongation of a specimen ΔL. A P–ΔL diagram is traced by a recording instrument or plotted from successive readings of the load and the corresponding increase in the length of the specimen. The forces measured at different instants during the testing are laid off to scale on the axis of ordinates, and the elongations on the axis of abscissas.
A diagram in these coordinates will, of course, depend on the dimensions of a specimen. The longer the specimen, the greater are the absolute elongations for one and the same force. In order to make these diagrams independent of the dimensions of test pieces and comparable for different materials, the ordinates should represent not forces but stresses 
obtained by dividing the tensile force by the original cross-sectional area 
of the specimen
.
The abscissas should represent strains rather than absolute elongations.
The points of the tension test diagram thus obtained characterize the state of the specimen at different instants, and the entire diagram gives the stress-strain relation for the specimen over the duration of the test, shows a tension test diagram of mild steel. We proceed to consider its characteristic points.
Proportional limit. Up to a certain state characterized by point A in the diagram, the 
relation is represented by a straight line. This is an indication of the fact that here elongations of the specimen increase directly as stresses. This straight line makes a very small angle with the axis of ordinates, i. e., and the elongations of the specimen increase slowly in this portion. Point A corresponds to the stress known as the proportional limit. Up to the proportional limit Hooke’s law holds good. Consequently, the proportional limit is defined as the maximum stress to which strains increase directly as stresses in the material. The stress corresponding to the proportional limit is designated as 
.
If we consider any state of the specimen within the straight-line portion of the diagram, such as the state represented by point, the slope of the straight-line portion to the axis of abscissas is given by the ratio where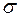 
is a concrete quantity and a pure number. On the other hand, according to Hooke’s law.
Consequently i. e., the numerical value of the modulus of elasticity of the first kind can be determined, with the proper use of scales for the diagram, as the slope of the straight-line portion to the axis of abscissas.
Elastic limit. In designing a structure it is sometimes important to know the stress at which the material first undergoes plastic action. Extremely precise measurements show that even highly elastic materials develop permanent deformations under very small stresses. But the magnitude of these permanent deformations is so small that they are of no practical significance. Permanent deformations increase with increasing stress. The elastic limit is defined as the stress at which the material develops a certain predetermined value of permanent strain (0,002 to 0,005 or 0,2 to 0,5 per cent of the original length of the specimen).
The elastic limit is designated as 
. The determination of the elastic limit presents great difficulties. It requires very precise and prolonged tests. In practice the magnitude of the elastic limit (for steel, for example) is very close to the proportional limit, and therefore point corresponding to the proportional limit is considered to be coincident with the point corresponding to the elastic limit. Further, as the stress increases, the tension test curve rises and departs from the straight line, turning smoothly to the right point.
Yield point (critical point). Some materials, such as mild steel, have a portion in the tension test diagram slightly above the proportional limit, from point on, in which elongations begin to increase without increase in stress. This phenomenon is called yielding. The yield point is defined as the stress at which a perceptible elongation occurs in the material without any increase of the stress. The yield point is designated as 
. The point of the diagram corresponding to the yield strength is called the critical point. Sometimes instead of a horizontal portion of the diagram there is even an inclined portion (sloping down to the right).
After passing the yield point the material recovers its ability to resist deformation but its elongation now begins to increase more rapidly than stresses, permanent deformations also increase rapidly. The yield point is a very important characteristic of the mechanical behavior of a material since stresses above the yield point produce impermissible permanent deformations.
Many materials, such as steel alloys, have no pronounced yield point. The tension test diagram of such materials passes smoothly from the elastic part to a part where large permanent deformations occur. The yield strength of such materials is established in a pure conventional manner. The yield strength for them is considered as the stress at which they develop a permanent set (offset) equal to a specified value. Therefore, when speaking of the yield strength of such materials it is necessary to indicate the corresponding permanent set. The yield strength is commonly taken as the stress corresponding to a permanent set of 0,2 per cent. When materials having a pronounced yield point are stretched, it is easy to observe the onset of yielding. If, for example, a tension testing machine is provided with a pointer indicating tensile forces, the pointer stops moving and remains on the same division for some time when the yield point of the material is reached though the deformations of the specimen continue to grow.
Also, the onset of yielding in the material can be noticed by observing the specimen itself. The polished surface of the specimen dulls[27] and gradually becomes lusterless when the yield point is reached. Under close examination the surface exhibits lines inclined at about 450 to the axis of the specimen. The number of these lines, known as Luders lines, increases gradually and in consequence the surface of the specimen becomes dull. The occurrence of these lines and their propagation throughout the length of the specimen are evidence of the shears produced in crystals of the material.
Ultimate strength. Beyond the yield point the tension test diagram becomes curved (principally convex upward) and, as already stated, the deformations of the specimen begin to grow more rapidly than the stresses. Point corresponds to the maximum value of the tensile force. The stress equal to the ratio of the maximum tensile force to the original cross-sectional area of the specimen is called the ultimate strength. The ultimate strength is designated as 
. After the ultimate strength is reached, a local reduction of area of the specimen, called necking, begins to occur gradually. During necking the specimen elongates mainly at the necked-down portion while the remainder of the specimen elongates only slightly.
Since during necking the cross section at the neck becomes smaller and smaller, the deformation of the specimen occurs with decreasing load. The ultimate strength is a very important strength characteristic of a material, particularly important for brittle materials, such as cast iron, hardened and cold-drawn steel, etc., which undergo relatively small deformations at fracture. At a stress corresponding to point the specimen ruptures. The stress at rupture lies below the ultimate strength in the tension test diagram. This is due to the fact that we agreed to calculate the stresses on the basis of the original cross-sectional area of the specimen. Actually, however, at the time of rupture the material develops the maximum stress since the area of the section becomes a minimum at that time. This stress is sometimes called the true ultimate strength.
The diagram considered above is termed an ordinary stress and strain diagram since the stresses are related to the original cross-sectional area and the elongations, to the original length. The cross section and length of the specimen vary continuously during the test. However, the ordinary diagram closely coincides with the true one up to the yield point. In the true diagram the ordinate is the stress obtained by dividing the force by the corresponding value of the minimum cross-sectional area of the specimen and the abscissa is the true unit elongation of the specimen, i. e., and the change in length divided by the length of the specimen at the current instant.
Ductility of material. Besides the yield point and the ultimate strength characterizing the mechanical properties of a material, a very important characteristic is ductility of the material. The ductility of the material is characterized by the magnitude of the percentage elongation and the percentage reduction of the cross-sectional area at rupture.
The percentage elongation at rupture is expressed as where 
is the length of the specimen after rupture and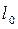 
is the original length.
The percentage reduction of the cross-sectional area is found from the expression where the cross-sectional area at the neck is after rupture and is the original cross-sectional area of the specimen.
It is customary to distinguish between ductile and brittle materials depending on whether permanent deformations occurring in the specimen at rupture are large or small, shows, for comparison, tension test diagrams of a ductile material (mild steel) and a brittle material (cast iron). It is seen that the brittle material fractures at a small strain and has no yield point. It should be noted, however, that the ductility of a material varies with the state of stress, strain rate, temperature and other conditions. A material exhibiting brittleness under tension at normal temperature may behave as a ductile material under other conditions, and conversely.
Consider the deformation of the specimen beyond the elastic limit. If the specimen is unloaded at some point of the diagram lying above the elastic limit, the line of unloading will be a straight line parallel to line. The segment represents the overall unit elongation of the specimen at the stress corresponding to point. The segment equal to represents the amount of plastic deformation which remains in the specimen after unloading. The strain beyond the elastic limit is made up of two parts; the elastic strain which disappears after removal of the load and the plastic strain which remains after unloading the specimen.
The elastic part of the strain beyond the elastic limit is proportional to the stress defined by segment.
Based on a so-called law of unloading, the elastic part of the strain can be determined beyond the elastic limit. Just before the rupture of the specimen its overall elongation is represented in the diagram by segment. After rupture the elastic part of the strain is recovered and only the permanent strain remains. The larger the permanent deformation, the more ductile is the material.
The Mechanical properties of metals as revealed in tests depend on the chemical composition of the material, temperature, heat treatment, speed of testing, etc.
The effects of chemical composition and heat treatment on mechanical properties are studied in metallographic analysis; here we shall briefly outline the effect of other factors on the mechanical properties of materials.
Temperature effect. The results of mechanical testing of materials usually relate to room temperatures (15-2000C) at which tests are conducted in laboratories. However, many parts even of one and the same machine operate in widely different temperature conditions. Thus, the exhaust valves of an automobile engine operate at 500 to 8000C while engine parts which are in direct contact with the environment sometimes operate at very low temperatures. For most materials the strength decreases and the ductility increases with increasing temperature. Mild steel behaves somewhat differently: at a temperature of about 250-300 0C the ultimate strength of the steel attains a maximum value but falls off sharply with further increase in temperature, diagrams showing the variation of the ultimate strength and ductility of steel with temperature. At high temperature, from 300-400 0C, metals continue to deform, though very slowly, at constant load. Strain rate increases with increasing load or temperature. This property of metals to deform continually at constant load and high temperature is called creep.[28]
Gas turbine blades operating at high temperature and subjected to centrifugal loads continually elongate with time. This elongation may cause the fracture of blades or dangerous brushing of these against the body, which sometimes happens in practice. Therefore, special steels and heat-resistant alloys exhibiting a small amount of creep are employed under these conditions.
At elevated temperatures the ultimate strength of a material depends also on the duration of testing. In these cases the strength of a material is referred to as creep-rupture strength, shows the creep-rupture strengths of a heat-resistant alloy at 700 0C, as is seen, the strength of the material falls with increasing time of testing.
As the temperature drops off, the strength of steel increases but the ductility sharply decreases. At low temperature steel is very sensitive to all kinds of vibrations and blows (cold brittleness of steel). An addition of nickel increases its resistance to impact loads at low temperatures.
Speed of testing. The mechanical characteristics of a material are also affected by the testing procedure. Therefore, to make the test results comparable it is necessary to follow a definite established testing procedure. Thus, for example, all metals possess the property of increasing their resistance to plastic deformation with increasing strain rate. Therefore, the more rapidly the specimen is loaded during testing, the higher are the resulting mechanical characteristics (proportional limit, yield point and ultimate strength) and the smaller the deformations. Steel possesses this property to a considerably lesser degree than more ductile metals such as zinc, lead, copper, etc.
The strain rate has its greatest effect on the yield point of a material. Under very rapid loading the yield stress may turn out to be higher than the ultimate strength obtained under slow loading. In view of this property of metals the rate of increase of stresses up to the yield point is usually not higher than 1000 N/cm2 per second under normal conditions of testing.
V. Strain Hardening
If, prior to tension testing, a specimen of mild steel is loaded to a stress below the elastic limit and unloaded, the test diagram of the specimen will be no different from the tension test diagram of a specimen not subjected to preloading. If, however, a specimen is previously loaded to a stress above the yield point, the mechanical properties of the specimens being compared will be different.
Let a specimen of mild steel be stretched to a stress characterized by point on the tension test. If the tensile load is now removed, a line is obtained, which is very close to a straight line. The elastic part of the overall elongation of the specimen disappears and a permanent elongation is observed. If the specimen is immediately stretched again, precise measurements will show that its proportional limit is lowered and the yield point is raised. The reloading is represented by line. The yield point becomes approximately equal to the stress to which the specimen was first stretched. If the specimen is allowed to “rest” for some time after loading and then stretched, the proportional limit rises again, i. e., the material recovers its elasticity, and the yield point is raised to a still greater extent. The complete recovery of elastic properties requires a certain length of time which depends on the kind of material. An increase in strength and a loss in ductility because of pre-stretching beyond the yield point are termed work hardening or strain hardening. Strain hardening changes the mechanical qualities of a material and residual stresses are set up in the material. In some cases the phenomena of strain hardening is undesirable and should be controlled, while in other cases strain hardening is artificially produced.
When holes are punched in a sheet for rivets, the materia1 at the edge of a hole undergoes strain hardening and becomes stiffer. This promotes the formation of cracks.
To avoid the detrimental effect of strain hardening in this case, the strain-hardened portion of the material is removed, increasing the hole diameter by drilling. The effect of strain hardening can also be eliminated by annealing, i. e., by heating the material to a certain temperature, holding it at that temperature for some time and subsequently slowly cooling. In other cases, as already stated, strain hardening is artificially produced. For instance, chains of lifting machines are pre-stretched above the yield point to make them less ductile and to avoid large deformations during operation, which would prevent the entry of the chain links in their seats on the drum.
Strain hardening is responsible for the fact that a wire obtained by drawing has a considerably higher strength than the steel from which it is made.
EXSERCISES
1. Write 10 questions to each part of the text.
2. Write out of the text the sentences with the verbs in the Passive voice.
3. Translate any part of the text (1500 signs) in writing.
4. Retell part I.
5. Speak on «Temperature effect».
