Resin transfer moulding (RTM)

УДК 539.3

ББК 30.121

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 3

UNIT I. MATERIALS. 4

UNIT II. TENSION AND COMPRESSION.. 14

UNIT III. WAT IS WHAT IN AVIATION.. 30

UNIT IV. ROTARY WING AIRCRAFT. 51

UNIT V. INTERNATIONAL AIRLINERS. 59

UNIT VI. COMPANY SUKHOI 66

UNIT VII. MIG-29 (MIKOYAN-GUREVICH) 80

UNIT VIII. ENGINES. 92

UNIT IX. OPTIMIZATION OF ENGINE. 99

UNIT X. RADAR.. 104

ENGLISH AND AMERICAN MEASURES. 112

ОБЯЗАТЕЛЬНЫЙ ЛЕКСИЧЕСКИЙ МИНИМУМ... 114

ЗАКЛЮЧЕНИЕ.. 121

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 122

ВВЕДЕНИЕ

Данное учебное пособие предназначено для студентов самолетостроительных специальностей университетов. Пособие разработано для курса дисциплины «Английский язык» по программе пролонгированного, профессионально направленного обучения и может быть использовано, как основное методическое пособие при обучении навыку чтения и говорения, формирования умения переводить специальные тексты технической направленности в рамках курса «Профессиональный английский» – для углублённого изучения предмета.

В пособии представлены тексты, компилированные из аутентичной литературы по таким направлениям самолётостроения как материалы, конструкция, характеристики, типы летательных аппаратов. Содержание текстов, отражающих специфику специальности, позволяет значительно расширить возможности будущих специалистов в процессе осуществления информационного поиска для решения исследовательских задач, задач модернизации современного наукоёмкого производства.

Тексты сопровождаются сносками, снимающими лексические трудности, в приложении представлены информация по способам перевода наиболее сложных грамматических явлений, что способствует повышению уровня адекватности перевода.

Интересные по содержанию и разнообразные по структуре тексты могут стать основой для диспута в рамках аудиторных занятий по дисциплине и выполнения творческих индивидуальных и групповых заданий.

UNIT I. MATERIALS

I. Materials

Composite materials

Composite materials (or composites for short) are engineered material made from two or more constituent materials with significantly different physical or chemical properties which remain separate and distinct on a macroscopic level within the finished structure.

History

Wood is a natural composite of cellulose fibers in a matrix lignin[1].The most primitive man made composite materials were strawand mud combined to form bricks for building construction; the Biblical Book of Exodus speaks of the Israelites being oppressed by Pharaoh, by being forced to make bricks without straw being provided. The ancient brick-making process can still be seen on Egyptian tomb paintings in the Metropolitan Museum of Art. The most advanced examples perform routinely on spacecraft in demanding environments. The most visible applications pave our roadways in the form of either steel and aggregate reinforced Portland cement [2] or asphalt concrete. Those composites closest to our personal hygiene form our shower stalls and bath tubs made of fiberglass. [3] Solid surface, imitation granite and cultured marble sinks and counter tops are widely used to enhance our living experiences.

Composites are made up of individual materials referred to as constituent materials. There are two categories of constituent materials: matrix and reinforcement. At least one portion of each type is required. The matrix material surrounds and supports the reinforcement materials by maintaining their relative positions. The reinforcements impart their special mechanical and physical properties to enhance the matrix properties. A synergism produces material properties unavailable from the individual constituent materials, while the wide variety of matrix and strengthening materials allows the designer of the product or structure to choose an optimum combination.

Engineered composite materials must be formed to shape. The matrix material can be introduced to the reinforcement before or after the reinforcement material is placed into the mold cavity or onto the mold surface. The matrix material experiences a melding event, after which the part shape is essentially set. Depending upon the nature of the matrix material, this melding event can occur in various ways such as chemical polymerization or solidification from the melted state.

A variety of molding methods can be used according to the end-item design requirements. The principal factors impacting the methodology are the natures of the chosen matrix and reinforcement materials. Another important factor is the gross quantity of material to be produced. Large quantities can be used to justify high capital expenditures for rapid and automated manufacturing technology. Small production quantities are accommodated with lower capital expenditures but higher labor and tooling costs at a correspondingly slower rate.

Most commercially produced composites use a polymer matrix material often called a resin solution. There are many different polymers available depending upon the starting raw ingredients. There are several broad categories, each with numerous variations. The most common are known as polyester, vinyl ester [4], epoxy [5], phenol [6], polyimide, polyamide, polypropylene, and others. The reinforcement materials are often fibers but also commonly ground minerals. The various methods described below have been developed to reduce the resin content of the final product, or the fiber content is increased. As a rule of thumb, lay up results in a product containing 60 % resin and 40 % fiber, whereas vacuum infusion gives a final product with 40 % resin and 60 % fiber content. The strength of the product is greatly dependent on this ratio.

Moulding [7] methods

In general, the reinforcing and matrix materials are combined, compacted and processed to undergo a melding event. After the melding event, the part shape is essentially set, although it can deform under certain process conditions. For a thermoset polymeric matrix material, the melding event is a curing reaction that is initiated by the application of additional heat or chemical reactivity such as organic peroxide. For a thermoplastic polymeric matrix material, the melding event is solidification from the melted state. For a metal matrix material such as titanium foil, the melding event is a fusing at high pressure and a temperature near the melt point.

For many molding methods, it is convenient to refer to one mold piece as a «lower» mold and another mold piece as an «upper» mold. Lower and upper refer to the different faces of the molded panel, not the mold's configuration in space. In this convention, there is always a lower mold, and sometimes an upper mold. Part construction begins by applying materials to the lower mold. Lower mold and upper mold are more generalized descriptors than more common and specific terms such as male side, female side, a-side, b-side, tool side, bowl, hat, mandrel, etc. Continuous manufacturing processes use a different nomenclature.

The molded product is often referred to as a panel. For certain geometries and material combinations, it can be referred to as a casting. For certain continuous processes, it can be referred to as a profile. Applied with a pressure roller, a spray device or manually. This process is generally done at ambient temperature and atmospheric pressure. Two variations of open moulding are Hand Lay-up and Spray-up.

Vacuum bag moulding

A process using a two-sided mould set that shapes both surfaces of the panel. On the lower side is a rigid mould and on the upper side is a flexible membrane or vacuum bag. The flexible membrane can be a reusable silicone material or an extruded polymer film. Then, vacuum is applied to the mould cavity. This process can be performed at either ambient or elevated temperature with ambient atmospheric pressure acting upon the vacuum bag. Most economical way is using a venture vacuum and air compressor or a vacuum pump.

Pressure bag moulding

This process is related to vacuum bag moulding in exactly the same way as it sounds. A solid female mould is used along with a flexible male mould. The reinforcement is placed inside the female mould with just enough resin to allow the fabric to stick in place. A measured amount of resin is then liberally brushed indiscriminately into the mould and the mould is then clamped to a machine that contains the male flexible mould. The flexible male membrane is then inflated with heated compressed air or possibly steam. The female mould can also be heated. Excess resin is forced out along with trapped air. This process is extensively used in the production of composite helmets due to the lower cost of unskilled labor. Cycle times for a helmet bag moulding machine vary from 20 to 45 minutes, but the finished shells require no further curing if the moulds are heated.

Autoclave moulding

A process using a two-sided mold set that forms both surfaces of the panel. On the lower side is a rigid mold and on the upper side is a flexible membrane made from silicone or an extruded polymer film such as nylon. Reinforcement[8] materials can be placed manually or robotically. They include continuous fiber forms fashioned into textile constructions. Most often, they are pre-impregnated with the resin in the form of prepreg fabrics or unidirectional tapes. In some instances, a resin film is placed upon the lower mold and dry reinforcement is placed above. The upper mold is installed and vacuum is applied to the mold cavity. The assembly is placed into an autoclave. This process is generally performed at both elevated pressure and elevated temperature. The use of elevated pressure facilitates a high fiber volume fraction and low void content for maximum structural efficiency.

Resin transfer moulding (RTM)

A process using a two-sided mold set that forms both surfaces of the panel. The lower side is a rigid mold. The upper side can be a rigid or flexible mold. Flexible molds can be made from composite materials, silicone or extruded polymer films such as nylon. The two sides fit together to produce a mold cavity. The distinguishing feature of resin transfer molding is that the reinforcement materials are placed into this cavity and the mold set is closed prior to the introduction of matrix material. Resin transfer molding includes numerous varieties which differ in the mechanics of how the resin is introduced to the reinforcement in the mold cavity. These variations include everything from vacuum infusion (for resin infusion see also Boat building) to vacuum assisted resin transfer moulding. This process can be performed at either ambient or elevated temperature.

Other

Other types of molding include press molding, transfer molding, winding, casting, centrifugal casting and continuous casting. There are also forming capabilities including CNC filament winding, vacuum infusion, wet lay-up, compression molding, and thermoplastic molding, to name a few. The use of curing ovens and paint booths is also needed for some projects.

Tooling [9]

Some types of tooling materials used in the manufacturing of composites structures include invar, steel, aluminum, reinforced silicone rubber, nickel, and carbon fiber. Selection of the tooling material is typically based on, but not limited to, the coefficient of thermal expansion expected number of cycles, end item tolerance, desired or required surface condition, method of cure, glass transition temperature of the material being molded, molding method, matrix, cost and a variety of other considerations.

II. Basic Types of Deformation

Deformation of structural and machine elements produced by external forces may be very complex. However, these complex deformations can always be represented as consisting of a small number of basic types of deformation.

The basic types of deformation of structural members which are studied in strength of materials are: tension,[10] compression, shear, torsion and bending.

Examples of complex deformations are provided by combined tension and torsion or combined tension and bending.

The above types of deformation will be considered in detail and methods for determining strains and stresses will be given in the relevant chapters of the book. It should be noted that strength of materials deals with only simple-shaped bodies. These are rods, plates and thin-walled shells.

A rod[11] is a body whose length is considerably greater than the transverse dimensions[12] which are of the same order of magnitude. Rods with straight axes are called bars, beams, columns, depending on their purpose.

A plate and a thin-walled shell are bodies whose thickness is considerably smaller than the other two dimensions. For instance, boilers, tanks, various vessels are thin-walled shells, the flat bottom of a boiler is a plate. Strength of materials deals mainly with rods. In the sequel we shall consider rods with straight axes and almost invariably of uniform section.

In machine design elements of complex shape are sometimes encountered. Such elements cannot be handled by the methods of strength of materials. However, most machine parts can be treated approximately as rods using the methods of strength of materials. The results thus obtained may be refined by experiment.

At presents, wide use is made in practice of experimental methods of strain measurement which make it possible to determine sufficiently stresses in complex-shaped members which do not lend themselves to theoretical calculation. In the first place mention should be made of the application of wire resistance strain gauges which indicate stresses through the change of electrical resistance.

Problems involving[13] the accurate determination of strains and stresses are dealt with in a science called the theory of elasticity. It uses rigorous mathematical methods. In practice, however, the design of machine and structural parts often does not require too much accuracy, it should be just sufficient but the methods of analysis should be simple and thus easy to apply. It is therefore customary in the design of machines and structures to use the methods of strength of materials which are considerably simper than those of the theory of elasticity and give sufficiently accurate results. There are, however, problems which are solvable only by the methods of the theory of elasticity, such as the determination of stresses in balls or rollers of bearings. A simplification of the methods of analysis in strength of materials is achieved by introducing some assumptions.

Both the theory of elasticity and strength of materials usually consider elastic deformations. In engineering practice, however, there are many cases where a material develops plastic deformations. Plastic defoliations are studied in a science called the theory of plasticity which has been extensively elaborated in the last few years.

III. Method of Sections. [14] Stress

As stated above, external forces acting on a body give to internal resisting forces. The external forces deform the body;[15] the internal forces tend to retain its original shape and volume.

To solve problems of strength of materials it is necessary to know how to determine internal forces and deformations in a body. The internal forces at any section of a body are determined by the method of sections. The idea of this method is as follows.

Consider a body which is in a state of equilibrium under the action of forces. If, for instance, we are interested in the internal forces acting at a section, we imagine the body cut through this section and one of the two parts removed, say, the right one. The remaining left-hand part will then be acted on by the external forces. In order for this part of the body to remain in equilibrium, it is necessary to apply internal forces over the entire section.

These forces represent the action of the removed right-hand part of the body on the remaining left-hand part. Being internal forces for the entire body, they play the role of external forces for the isolated part. The magnitude of the resultant of the internal forces can be determined from the condition of equilibrium[16] of the isolated part. The law of distribution of internal forces over the section is not in general known. To solve this problem, it is necessary to know in each particular case how the body deforms under the action of external forces. Thus, the method of sections only allows us to determine the sum of the internal forces acting at the section in question. The sum of these forces may reduce to a single force, to a couple or, in the general case, to a force and a couple.

If an infinitesimal[17] area ΔA is isolated at the section, it may be said, assuming the internal forces to be acting at all points in the section, that this area is acted on by an infinitesimal force ΔP. The ratio of the internal force ΔP to the magnitude of the isolated area ΔA gives the average stress on this area

.

Thus, the stress (which characterizes the intensity of internal forces) is defined as the force per unit area. The stress is expressed in newtons per square metre (N/m²). Reducing the area to zero, i. e., passing to the limit, we obtain the true stress at a given point, say, the centre of the area ΔA. Consequently, the true stress at a given point is

.

If the internal forces (elastic forces) are known to be uniformly distributed over the section, in this simplest case the stress is calculated by dividing the total elastic force acting at the section by the entire cross-sectional area, i. e.,

.

Since the force has a direction, the stress will also have a direction. In the general case, the stress () on a given area will make an angle with this area. Resolving this stress into two components, one being perpendicular to the area, called the normal stress and designated by the letter (sigma), and the other lying in the plane of the area, called the shearing (or tangential) stress and designated by the letter 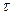(tau), we obtain

, .

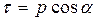The total stress is expressed in terms of the normal and shearing stresses by the following formula

.

The total stress is not considered to be a convenient measure of internal forces in a body as materials resist normal and shearing stresses in different ways. Normal stresses tend to bring closer together or separate individual particles of a body in the direction of the normal to the plane of the section. Shearing stresses tend to move particles of a body with respect to each other on the plane of the section.

In determining the stress at any point of a body, it is possible to pass an infinite number of differently oriented planes through this point. To fully characterize the state of stress at a given point, we have to know not only the magnitude and direction of the stress but also the inclination of the plane. In the following we shall see how the stress at a given point varies with the inclination of a plane passed through this point. The concepts of strain and stress are the fundamental concepts in strength of materials.

EXSERCISES

1. Write 10 questions to each part of the text.

2. Write out of the text the sentences with the verbs in the Passive voice.

3. Translate any part of the text (1500 signs) in writing.

4. Retell part II.

5. Speak on Moulding[18] methods