Определители
Каждой квадратной матрице 
можно поставить в соответствие единственное число, называемое определителем или детерминантом матрицы, которое обознается символом (1):
. (1)
В этом случае перечисляются все элементы матрицы А, для которой он определяется. Элементы матрицы, строки и столбцы в этом случае называются элементами, строками, столбцами определителя.
В тех случаях когда элементы матрицы А уже указаны выше или её числовые значения не имеют принципиального значения, используется более краткий вариант обозначений: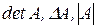 
.
Общая формула для расчета определителей матриц порядка n опирается на следующие понятия: перестановки и транспозиции элементов множества. Поэтому сначала введем их.
Пусть X – некоторое множество из n элементов.
Определение 1. Множество из n элементов называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число от 1 до n, номер элемента.
Определение 2. Различные упорядоченные множества одного и того же множества из n элементов называются перестановками этого множества.
Теорема 1. Число перестановок множества из n различных элементов равно 
Доказательство. Воспользуемся методом математической индукции.
1 шаг. Докажем справедливость утверждения при n = 2.
В этом случае множество состоит из двух элементов, которые условно можно обозначить: a и b. Очевидно, что их можно перенумеровать (расставить) двумя способами: 
или 
. Так как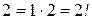 
, утверждение – верно.
2 шаг. Предположим, что утверждение верно при 
, т.е. множество из к различных элементов можно перенумеровать (расставить) 
способами.
3 шаг. Опираясь на предположение, выдвинутое на 2 шаге, докажем справедливость утверждения при 
.
Первый номер можно поставить в соответствие любому из элементов данного множества, т.е. имеется 
способ. Для каждого из возможных вариантов выбора остается перенумеровать k оставшихся элементов, а это, согласно выдвинутому на втором шаге предположению, возможно осуществить способами. Таким образом, число различных перестановок множества из 
различных элементов будет равно: 
. Формула остается верной.
Утверждение доказано.
Пусть множество Х состоит из элементов 
.
Обозначим символом 
произвольную перестановку элементов данного множества, здесь 
, 
принимает только одно из значений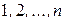 
. Перестановку вида 
, где элементы множества Х расположены в порядке возрастания, будем называть основной.
Определение 2. Операция, при которой два элемента перестановки (не обязательно стоящие рядом) меняются местами, называется транспозицией.
Пусть 
- число транспозиций, необходимых для получения перестановки из основной.
Определение 3. Определителем или детерминантом матрицы называется число, определяемое по правилу 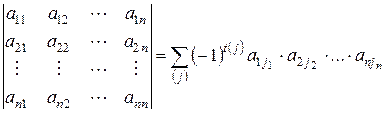(2):
. (2)
Это сумма по всем перестановкам множества из элементов , которая содержит слагаемых, каждое из которых представляет собой произведение сомножителей, содержащих ровно по одному элементу из каждой строки и каждого столбца матрицы, взятых со знаком плюс или минус в зависимости от четности числа транспозиций, необходимых для получения соответствующей перестановки из основной.
Из формулы (2) легко получаются формулы для расчета определителей первого, второго и третьего порядков. Представим их в виде, наиболее удобном для практического применения.
, (3)
т.е. величина определителя первого порядка равна элементу, из которого он состоит. Например, 
.
. (4)
Определитель второго порядка равен разности значений произведений элементов главной и побочной диагоналей.
Пример 1. Вычислите определитель второго порядка 
.
Решение. Согласно формуле (4),
.
Формула для вычисления определителя третьего порядка (5) уже содержит 6 слагаемых (3!=1×2×3=6):
(5)
Нетрудно заметить, что в формуле (5) первые три слагаемых, сохраняющих свой знак) – произведения элементов главной диагонали и двух треугольников, которые около неё можно образовать (смотрите рисунок 1), а слагаемые, входящие с формулу с противоположным знаком, - произведения элементов побочной диагонали и двух треугольников, которые около неё можно образовать (смотрите рисунок 2).
Рисунок 1 – Алгоритм, получения слагаемых, входящих в формулу (5) с сохранением знака
Рисунок 2 – Алгоритм, получения слагаемых, входящих в формулу (5) с противоположным знаком
Пример 2. Вычислите определитель третьего порядка: 
Решение. Согласно формуле (5), поучаем, что
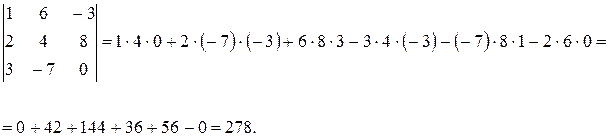
Замечание. Формула для определителей четвертого порядка содержит уже 24 слагаемых (
) и на практике, как правило, не используется. Вычисление определителей порядка 
осуществляется другими методами, которые следуют из свойств определителей.
Теорема 2. При транспонировании величина определителя не изменяется, т.е. 
.
Доказательство. Проведите самостоятельно, опираясь на формулу (2).
Замечание. Из теоремы 1 следует, что столбцы и строки определителя обладают одинаковыми свойствами. Поэтому, формулируя ниже свойства определителей, доказательство будем проводить только для строк, так как справедливость соответствующих свойств для столбцов легко доказать, применяя дважды операцию транспонирования.
Теорема 3. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
Доказательство. Пусть некоторая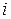 
-я строка определителя состоит из нулей, т.е. 
, тогда в формуле (2) в каждом слагаемом множитель, соответствующий данной строке: 
, 
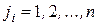, и, следовательно, каждое слагаемое в формуле (2) равно нулю и определитель равен нулю.
Следствие 1. Если один из столбцов определителя состоит из нулей, то определитель равен нулю.
Доказательство. Проведите самостоятельно.
Теорема 4. При перестановке двух строк определитель меняет свой знак.
Доказательство. Проведите самостоятельно.
Следствие 2. При перестановке двух столбцов определитель меняет свой знак.
Доказательство. Проведите самостоятельно.
Теорема 5. Определитель, содержащий две одинаковые строки равен нулю.
Доказательство. Пусть у матрицы А строки с номерами i и к состоят из одинаковых элементов. Пусть 
- матрица, получающаяся из матрицы А перестановкой этих двух строк.
Тогда, с одной стороны, из свойств определителей, смотрите теорему 4, следует, что
, (6)
с другой стороны, так как 
, строки состояли из одинаковых элементов,
. (7)
Из равенства (7) следует, что
.
Теорема доказана.
Следствие 3. Определитель, содержащий два одинаковых столбца, равен нулю.
Доказательство. Проведите самостоятельно.
Теорема 6. Если все элементы некоторой строки определителя умножить на некоторое число 
, то сам определитель умножится на число .
Доказательство. Умножая все элементы k -ой строки матрицы на число , получаем новую матрицу 
, у которой 
.
Теорема доказана.
Следствие 4. Если все элементы некоторого столбца определителя умножить на некоторое число , то сам определитель умножится на число .
Доказательство. Проведите самостоятельно.
Замечание. Из теоремы 5 и следствия 4 вытекает следующее правило: общий множитель элементов некоторой строки (столбца) определителя можно выносить за знак определителя.
Теорема 7. Определитель, содержащий две пропорциональные строки, равен нулю.
Доказательство. Пусть у матрицы 
, 
, где - некоторое постоянное число, т.е. элементы k -ой и m -ой строк пропорциональны. Вынося общий множитель элементов k -ой строки за знак определителя, мы получим, что
,
где , 
, , т.е. у матрицы две одинаковые строки и, следовательно, на основании теоремы 5,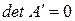 
, а значит, 
. Теорема доказана.
Следствие 5. Определитель, содержащий два пропорциональных столбца, равен нулю.
Доказательство. Проведите самостоятельно.
Теорема 8. Если все элементы некоторой i -ой строки определителя n- го порядка представлены в виде суммы двух слагаемых:
, ; (8)
то данный определитель равен сумме двух определителей, у которых все строки, кроме i -ой строки, такие же, как и в заданном определителе, а i -ая строка в одном определителе состоит из элементов 
, а в другом – из элементов 
, :
.
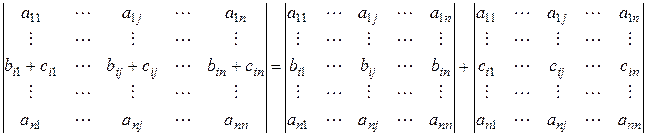Доказательство. Из (8) следует, что в формуле (2) множители, соответствующие элементам данной i -ой строки, имеют вид: 
. И следовательно,
.
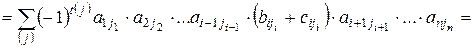
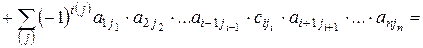
Теорема доказана.
Следствие 6. Если все элементы некоторого j -го столбца определителя n- го порядка представлены в виде суммы двух слагаемых:
, 
; (9)
то данный определитель равен сумме двух определителей, у которых все столбцы, кроме j -го столбца, такие же, как и в заданном определителе, а j -ый столбец в одном определителе состоит из элементов , а в другом – из элементов , :
.
Доказательство. Проведите самостоятельно.
Теорема 9. Определитель не изменяется, если к элементам одной из его строк прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
Доказательство. Пусть к элементам m - ой строки матрицы прибавляются элементы k -ой строки этой матрицы (
), умноженные на коэффициент . Получим новую матрицу 
, у которой 
; .
Из теоремы 8 в этом случае следует, что 
, где первый определитель совпадает с исходным, а второй содержит две пропорциональные строки, и, следовательно, равен нулю (теорема 7). Таким образом, 
.
Теорема доказана.
Следствие 7. Определитель не изменяется, если к элементам одного из его столбцов прибавить соответствующие элементы другого столбца, умноженные на одно и то же число.
Доказательство. Проведите самостоятельно.
Замечание. Очевидно, что можно не только складывать элементы, но и вычитать, так как вычитание – прибавление элементов умноженных на (-1).
Рассмотренные выше свойства определителей позволяют упростить расчеты.
Пример 3. Вычислите определитель 
.
Решение.
Кроме того, они являются основным инструментом при доказательстве тождеств.
Пример 4. Докажите тождество: 
.
Решение.
Тождество доказано.
Определение 4. Дополнительным минором к элементу 
определителя n -го порядка (1), называется определитель порядка 
, получаемый из исходного, вычеркиванием i -й строки и j- го столбца.
Обозначение: 
.
Например, для определителя 
дополнительным минором к элементу 
является определитель 
, а дополнительным минором к элементу 
является определитель 
.
Определение 5. Алгебраическим дополнением к элементу определителя n -го порядка (1), называется число, определяемое по правилу: 
.
Обозначение: 
.
В частности, для определителя , рассмотренного выше, алгебраическим дополнением к элементу является число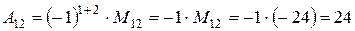 
, а алгебраическим дополнением к элементу является число 
.
Теорема 10. Сумма произведений элементов любой строки определителя на алгебраические дополнения к ним равна величине определителя:
Доказательство. Проведите самостоятельно.
Следствие 8. Сумма произведений элементов любого столбца определителя на алгебраические дополнения к ним равна величине определителя:
Доказательство. Проведите самостоятельно.
Замечание. Теорема 10 и следствие 8 дают основное практическое правило для вычисления определителей порядка , которое называется методом разложения по элементам строки или столбца определителя:
(10)
(11)
Пример 5. Вычислите определитель 
.
Решение.
1 способ. Воспользуется методом разложения по элементам первой строки.
.
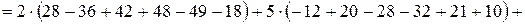
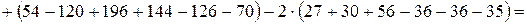
Очевидно, что выбор столбца или строки, по которым ведется разложение, в данном случае не имеет принципиального различия, так среди элементов нет нулевых, и при любом выборе расчет сведется к вычислению четырех определителей третьего порядка.
2 способ. Предварительно преобразуем исходный определитель, а точнее добьемся того, чтобы все элементы в третьем столбце за исключением одного оказались равными нулю. Для чего к элементам второй строки прибавим элементы первой строки, к элементам третьей строки прибавим элементы первой строки, умноженные на (-2) и затем к элементам четвертой строки прибавим элементы первой строки, умноженные на (-1). Согласно теореме 9 величина определителя при этом не изменится. Запишем расчеты, выполняя указанные действия последовательно.
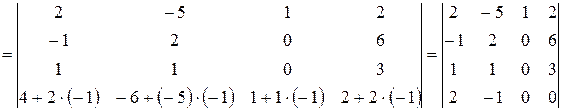
В получившемся определителе 
среди элементов третьего столбца только один отличен от нуля, поэтому для дальнейших расчетов разумно воспользоваться методом разложения по элементам третьего столбца.
.
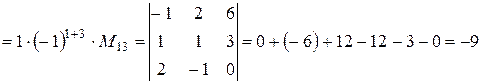Замечание. Правило вычисления определителей методом разложения по элементам строки или столбца позволяет получить особую формулу для вычисления определителей треугольного вида.
Следствие 9.
. (12)
(величина определителя треугольного вида равна произведению элементов, стоящих на главной диагонали).
Доказательство. Данное утверждение легко доказать, опираясь на метод математической индукции.
1 шаг. Проверим основание для проведения индукции.
.
.
2 шаг. Предположим, что формула верна при , т.е.
.
3шаг. Докажем, что формула остается в этом случае справедливой и для . Применяя к определителю порядка 
метод разложения по элементам последней строки и учитывая, что в этой строке все первые k элементов равны нулю, получаем
,
т.е. формула сохраняет свой вид. Утверждение доказано.
Следствие 10. Величина определителя единичной матрицы любого порядка равна 1.
Доказательство. Проведите самостоятельно.
Замечание. Следствие 9 дает еще один алгоритм вычисления определителей порядка : определитель, используя возможность преобразования элементов, нужно предварительно привести к треугольному виду, а затем воспользоваться формулой (12).
Пример 6.Вычислите определитель.
Решение.
.
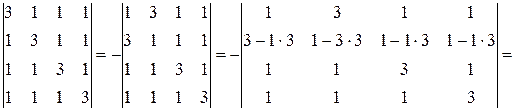
Теорема 11. Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения к элементам другой строки определителя равна нулю, т.е.
, 
, 
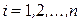. (13)
Доказательство. Рассмотрим определитель n- го порядка вида (1) и зафиксируем у него произвольным образом две строки i и k:
.
Составим новый определитель порядка n, заменяя все элементы k -ой строки соответствующими элементами i -ой строки:
.
Тогда, с одной стороны он равен нулю, как определитель, содержащий две одинаковые строки, с другой стороны, разлагая его по элементам к -ой строки, получаем, что его величина равна: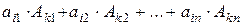 
, где 
- алгебраические дополнения к элементам к -ой исходного определителя. Это связано с тем, что данные опредлители отличаются только элементами k-ой строки, а вычисление алгебраических дополнений к элементам этой строки они не влияют. Таким образом, 
.
В силу произвольности выбора строк результат будет справедлив для любых 
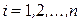, , . Теорема доказана.
Следствие 11. Сумма произведений элементов некоторого столбца определителя на соответствующие алгебраические дополнения к элементам другого столбца определителя равна нулю, т.е.
, 
, . (14)
Доказательство. Проведите самостоятельно.
Теорема 12. Для любых квадратных матриц А и В одинакового порядка определитель произведения матриц равен произведению их определителей:
. (15).
Доказательство.
Покажем справедливость этого утверждения при 
.
Пусть
, тогда 
.
Что и требовалось доказать. Справедливость утверждения в общем виде докажите самостоятельно.
Определение 6. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. В противном случае, т.е. если определитель матрицы равен нулю, она называется вырожденной.
