Цифровые автоматы. Основные два вида ЦА. Обощенная схема ЦА. Основные этапы
Проектирования ЦА, с краткой характеристикой каждого этапа. Способы описания
поведения ЦА (таблица переходов, граф переходов).
Автоматами, или последовательностными (не последовательными!) схемами,
называют схемы, выходы которых зависят не только от значений входов в данный
момент, но и от комбинаций значений входов в определенные прошлые моменты времени.
Тем или иным содержимым памяти автомата определяется его внутреннее
состояние, или просто состояние. Внешнее проявление различных состояний—это
различные реакции автомата на одни и те же воздействия.
Существует два основных вида цифровых автоматов:
 Цифровой автомат Мура;
Цифровой автомат Мура;
 Цифровой автомат Мили;
Цифровой автомат Мили;
Первый – его выходной сигнал не зависит от входного, вернее зависит, но косвенно, а работа цифрового автомата определяется его состоянием.
Второй – имеет общий тип. Это значит, что его новое состояние и выходное значение зависит от текущего состояния и входного значения.
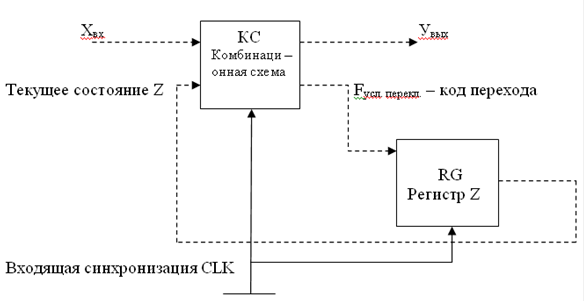
Выходной код Y, вырабатываемый КС, есть функция не только входного кода X, но и кода состояния
Z, который хранится в регистре состояний RG Z. Этот регистр и есть память автомата.
Чем больше его емкость, тем богаче спектр поведения автомата, шире разнообразие его
реакций на одни и те же входные воздействия, полнее учет прошлого опыта. Новое
состояние Zi+1, в которое переходит автомат после очередного входного воздействия, т.е.
новое содержимое RG Z, задается кодом перехода F.
Задачу синтеза автомата средней сложности удобно разбить на три части:
формализация задания, кодирование состояний, синтез комбинационной схемы.
Формализация задания автомата
Задание уточняется, корректируется
Чтобы проиллюстрировать характер возникающих при синтезе автомата вопросов, процедура синтеза будет излагаться на примере простого объекта с хорошо понятными алгоритмом
построение предварительного, упрощенного графа или таблицы автомата (синтез абстрактного автомата)
Кодирование состояний
Минимально возможное число
триггеров равно ближайшему сверху целому от двоичного логарифма числа состоянии.
Максимальное число триггеров равно числу состояний, при этом каждое состояние
кодируется единицей в одном из триггеров. В среднем с ростом числа триггеров в
пределах указанного диапазона уменьшается число логических элементов, требующихся
для дешифрации состояний.
Синтез комбинационной схемы


Во-первых, конфликтующим входным сигналам были присвоены приоритеты. Чем
выше приоритетность некоторого сигнала, тем больше в таблице на строке, где этот
сигнал проявляется, крестов (X), а каждый крест, относящийся к какой-то переменной,
отображает сразу две строки — и для значения этой переменной 0, и для значения 1
Во-вторых, в качестве триггеров использованы JK-триггеры, которые при J=К=0
хранят свое состояние. Следовательно, все строки с такими комбинациями входов КС,
которые не вызывают смены состояния автомата, т. е. переключения триггеров, можно в
таблицу не вносить: все равно на выходе КС они дают нули и поэтому в состав СДНФ не
войдут
Граф и таблица—два взаимно эквивалентных способа формального описания
поведения автомата. Каждый из них задает реакцию проектируемого автомата на каждый
входной сигнал уже однозначно, без опасности разночтения. Чтобы граф был строго
эквивалентен таблице, на нем нужно изобразить в явном виде все петли.

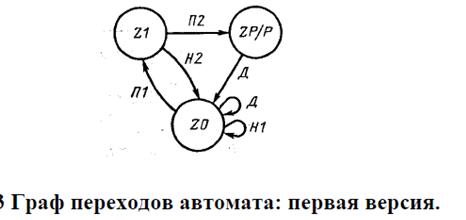
Описанный процесс построения графа или таблицы называют этапом абстрактного
синтеза автомата или этапом синтеза абстрактного автомата. Абстрактный автомат — это математическая модель, это алгоритм функционирования некоторого преобразователя кодовых последовательностей.






