Решение и приведение дифференциальных уравнений относительного движения двух ЛА

ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ

ДВУХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ

В ОКРЕСТНОСТИ КРУГОВОЙ ОРБИТЫ.

Уравнения движения двух летательных аппаратов.

Уравнение движения ЛА в геоцентрической инерциальной системе коор­динат (в предположении центральности гравитационного поля) имеет вид

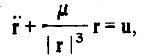
где u - вектор ускорения, сообщаемого ЛА, например, двигателем.

Рассмотрим движение двух ЛА, причем будем считать, что один из них (назовем его пассивным) движется по невозмущенной кеплеровой орбите, а другой (активный, или маневрирующий) - по орбите, которая может отли­чаться от первой как за счет начального рассогласования между орбитами, так и за счет действия возмущающего ускорения. Уравнения движения этих ЛА соответственно

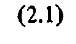
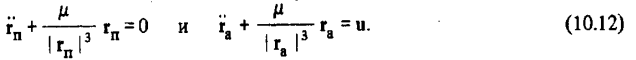
Введем понятие вектора относительной дальности между летательными
аппаратами

и получим уравнения относительного движения.

В исходной инерциальной системе координат 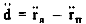или в соот­ветствии с (2.1)

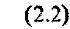
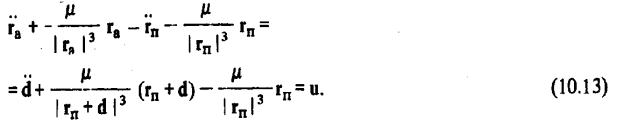
Предположим, что пассивный ЛА движется по круговой орбите радиуса , и осуществим перевод уравнения из исходной инерциаль­ной системы координат в орбитальную систему, начало которой совпадает с центром масс пассивного ЛА и которая вместе с ним вращается в инерциальном пространстве с угловой скоростью орбитального движения

 

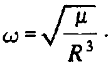
Уравнения движения в орбитальной системе координат.

Орбитальная система координат (ОСК) является декартовой (рис. 2.1), ее ось Ох направлена вдоль орбитальной скорости пассивного ЛА, ось Оу -вдоль геоцентрического радиуса-вектора пассивного ЛА, а ось Oz до­полняет систему до правой.

Рис. 2.1. Орбитальная декартова объектоцентричес­кая система координат.

 

Вектор относительной дальности между летательными аппаратами, век­тор скорости изменения этой дальности, геоцентрический радиус-вектор пассивного ЛА и вектор его угловой скорости имеют в ОСК следующие компоненты:

 

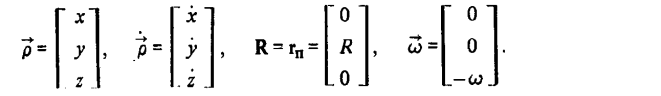
Зависимость между относительными ускорениями в инерциальной систе­ме и ОСК дается выражением 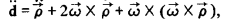которое после проведения операций векторного умножения принимает вид

 

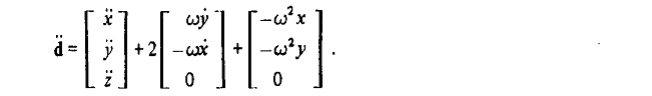
Учитывая зависимости

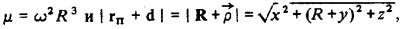получаем из (2.2) дифференциальные уравнения относительного движе­ния в покомпонентной форме:

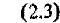
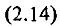
Решение и приведение дифференциальных уравнений относительного движения двух ЛА.

Система (2.3) является системой точных дифференциальных уравне­ний движения активного ЛА относительно пассивного в ОСК, которая дви­жется вместе с пассивным ЛА по круговой орбите. Орбита, с которой связа­на ОСК, обычно называется опорной орбитой.

Предполагая, что компоненты вектора относительной дальности р малы по сравнению с величиной R, разложим выражение

 

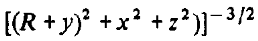
в ряд и ограничимся несколькими членами этого разложения:

 

В соответствии с полученным разложением система (2.3) приводится к виду

 

 

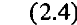
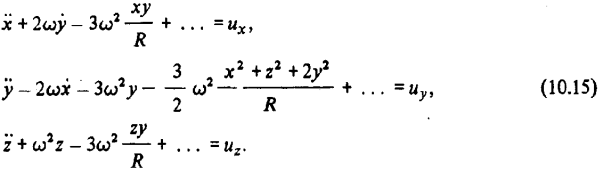
Если в системе (2.4) оставить только записанные члены разложения, мы получим систему второго приближения к точной системе (2.3), поскольку в ней учтены члены до второго порядка относительно компо­нент вектора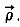

 

Первое или линейное приближение к (2.3) имеет вид

 

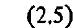
Наиболее простой вид оно имеет только при отсутствии возмущающего ускорения (u = 0) или при постоянстве величины ускорения и задании специального закона его ориентации:

-ориентация вектора ускорения в ОСК постоянна, т.е. изменяется от­носительно инерциального пространства с угловой скоростью враще­ния ОСК;

- ориентация вектора ускорения в инерциальном пространстве постоян­на, т.е. изменяется в ОСК с угловой скоростью, обратной угловой скорости вращения ОСК.

Решение системы (2.5) при u = 0, соответствующее случаю невозму­щенного относительного движения, имеет вид:

 

 

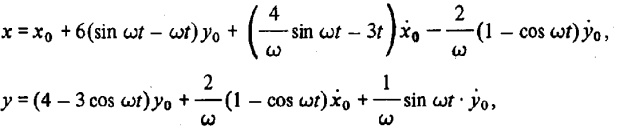
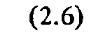
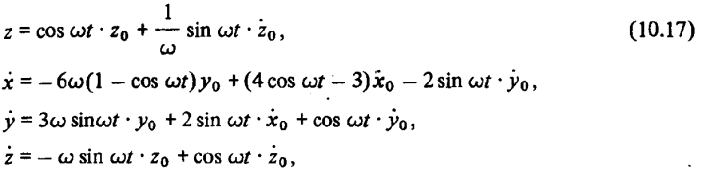
где 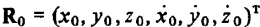— вектор состояния относительного движе­ния в начальный момент 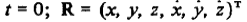— вектор состояния, характеризующий относительное движение в произвольный текущий мо­мент t.

Более удобно и компактно решение (2.6) может быть записано в матрично-векторном виде

 

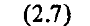где 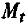— матрица размера 6X6 коэффициентов при компонентах начально­го вектора состояния 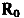в (2.6).

Матрицу 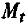, называют матрицей прогноза, поскольку она осуществляет операцию преобразования начального вектора состояния 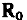в вектор состояния R, соответствующий интересующему нас моменту (в будущем или в прошлом). Элементы матрицы для заданной опорной орбиты явля­ются функциями лишь времени прогноза г.

Особенностью решения системы линейного приближения (2.6) являет­ся независимость уравнений, характеризующих движение в плоскости опор­ной орбиты (компоненты х, у), и уравнений, характеризующих боковое движение (компонента z).

В случае возмущенного относительного движения при специальном зако­не ориентации возмущающего ускорения решение системы дифферен­циальных уравнений (2.5) также может быть записано в матрично-векторном виде

 

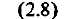где 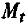— матрица прогноза при невозмущенном относительном движении; At — матрица размера 6X3, элементы которой являются функциями вре­мени прогнозирования и имеют различный вид для каждого из двух указан­ных выше аконов орентации вектора возмущающего ускорения.