При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Абсолютный прирост - абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.
Темп роста - относительный показатель, характеризующий интенсивность процесса роста (снижения). Он показывает, сколько процентов составляет уровень данного периода по сравнению с базисным или предыдущим уровнем, т.е. характеризует относительную скорость изменения уровня ряда в единицу времени. Темп роста всегда представляет собой положительное число.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы).
Темп прироста - относительный показатель, характеризующий величину прироста (снижения). Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста).
Абсолютное значение одного процента прироста показывает, какое абсолютное значение скрывается за относительным показателем - одним процентом прироста. Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня.
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным,а уровень, с которым производится сравнение, - базисным.
Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.
Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.
Показатели анализа рядов динамики и формулы их расчета приведены таблице 7.5.
Таблица 7.5 - Основные показатели анализа ряда динамики
| № п/п | Показатель | Базисный | Цепной |
| 1. | Абсолютный прирост (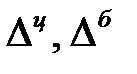 ) )
|  ; ;
 - уровень сравниваемого периода, - уровень сравниваемого периода,
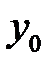 - уровень базисного периода - уровень базисного периода
| 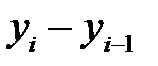 ; ;
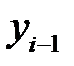 - уровень предшествующего периода - уровень предшествующего периода
|
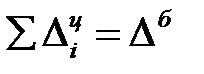
| |||
| 2. | Коэффициент роста (снижения) (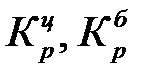 ) )
| 
| 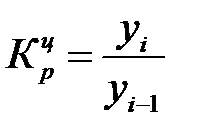
|
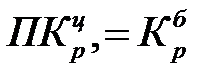
| |||
| 3. | Темп роста (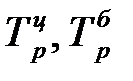 ) )
| 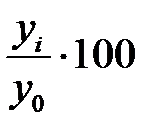
| 
|

| |||
| 4. | Темпы прироста (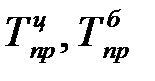 ) )
| 
| 
|
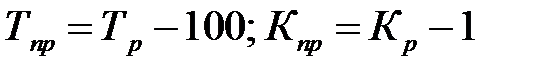
| |||
| 5. | Абсолютное значение одного процента прироста (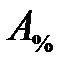 ) )
| - | 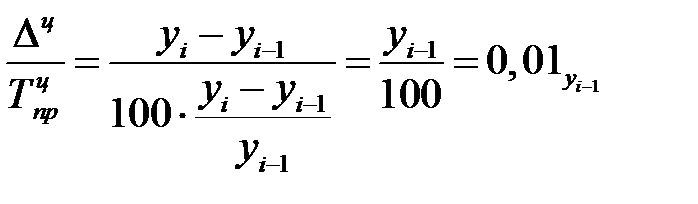
|
В таблице 7.6. приведены результаты расчета показателей, характеризующих динамику производства электроэнергии в РФ за период 2002-2007.
Таблица 7.6 - Динамика производства электроэнергии в РФ
| Год | Производство лектроэнергии, млрд. кВт  ч ч
| Абсолютный прирост, млрд. кВт  ч ч
| Коэффициенты  роста роста
| Темпы прироста, % |  
| |||

| 
| 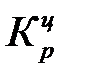
| 
| 
| 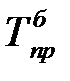
| |||
| - | - | - | - | - | - | - | ||
| 1,03 | 1,03 | 8,91 | ||||||
| 1,02 | 1,05 | 9,16 | ||||||
| 1,02 | 1,07 | 9,32 | ||||||
| 1,04 | 1,12 | 9,53 | ||||||
| 1,02 | 1,14 | 9,96 | ||||||
| Итого: 5703 | 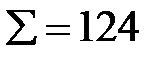
| - | 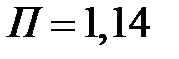
| - | - | - | - |
Цепные и базисные абсолютные приросты показывают прирост (сокращение) производства электроэнергии РФ по годам и абсолютное изменение по сравнению с 2002 г.
Сумма последовательных цепных абсолютных приростов равна базисному приросту, т.е. общему приросту за весь промежуток времени (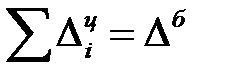 ). Так, в нашем случае:
). Так, в нашем случае:
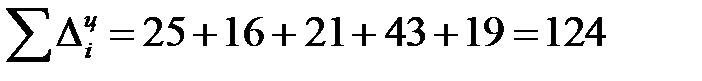 .
.
Цепные и базисные коэффициенты роста характеризуют интенсивность изменения производства электроэнергии в России по годам и за весь период.
Между цепными и базисными коэффициентами роста существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период (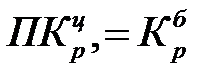 ).
).
Проверим взаимосвязь цепных и базисных коэффициентов роста на нашем примере: 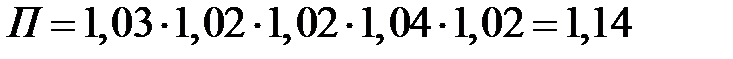 .
.
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения).
В нашем примере мы видим, что рост производства электроэнергии колеблется ежегодно от 2 до 4%. В целом же за рассматриваемый период (2002 – 2007гг.) рост электроэнергии составил 14%.
При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста (см. табл. 7.5). Этот показатель называют абсолютным значением одного процента прироста.
В нашем примере (см. табл. 7.6) абсолютное значение 1% прироста производства электроэнергии в России в 2002 - 2007 гг. увеличивалось.
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда исредние показатели изменения уровней ряда.
Средний уровень ряда характеризует обобщённую величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.
Методы расчета среднего уровня интервального и моментного рядов динамики различны.
Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется:
1) при равных интервалах по формуле средней арифметической простой:
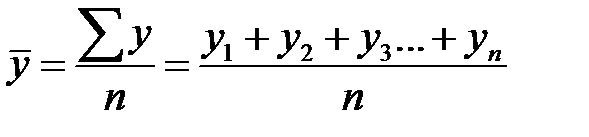 , (7.1)
, (7.1)
где 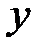 - абсолютные уровни ряда;
- абсолютные уровни ряда;
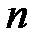 - число уровней ряда.
- число уровней ряда.
2) при неравных интервалах по формуле средней арифметической взвешенной:
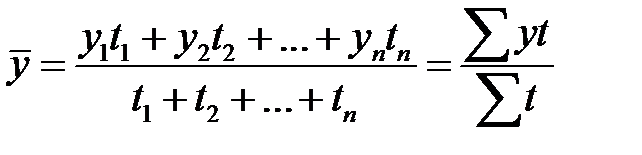 , (7.2)
, (7.2)
где  - уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени
- уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени 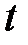 ;
;
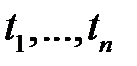 - веса, длительность интервалов времени (дней, месяцев) между смежными датами.
- веса, длительность интервалов времени (дней, месяцев) между смежными датами.
Средний уровень производства электроэнергии за 2002 - 2007 гг. находим по формуле (7.1), так как исследуемый ряд динамики представляет собой интервальный ряд с одинаковыми интервалами, млрд. кВт ч:
 .
.
Расчет среднего уровня для интервального ряда динамики с неравностоящими уровнями рассмотрим на примере.
Пример 7.2. Если известно, что с 1-го по 15-е число месяца в акционерном коммерческом банке работали 20 человек, с 16-го по 25-е - 27 человек, а с 26-го по 30-е - 30 человек, то среднесписочное число работников за месяц составит, чел.:
 .
.
Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формулесредней хронологической:
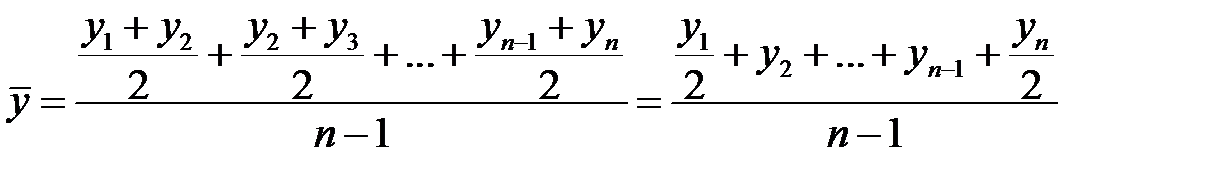 , (7.3)
, (7.3)
где  - уровни периода, за который делается расчет;
- уровни периода, за который делается расчет;
 - число уровней;
- число уровней;
Пример 7.3. Пусть имеются данные о валютном курсе, установленном ЦБ РФ первое число каждого месяца.
Требуется определить средний месячный курс доллара в 4 квартале 2009г.
Таблица 7.7 - Котировка доллара США, руб. за 1 доллар
| Дата | 1.01.2009г. | 1.02.2009г. | 1.03.2009г. | 1.04.2009г. |
| Курс доллара, руб | 29,40 | 35,41 | 35,72 | 34,32 |
Требуется определить средний месячный курс доллара в 4 квартале 2009г.
Так как 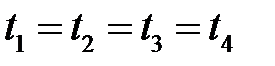 , для расчета применяем формулу (7.3), руб./долл.:
, для расчета применяем формулу (7.3), руб./долл.:
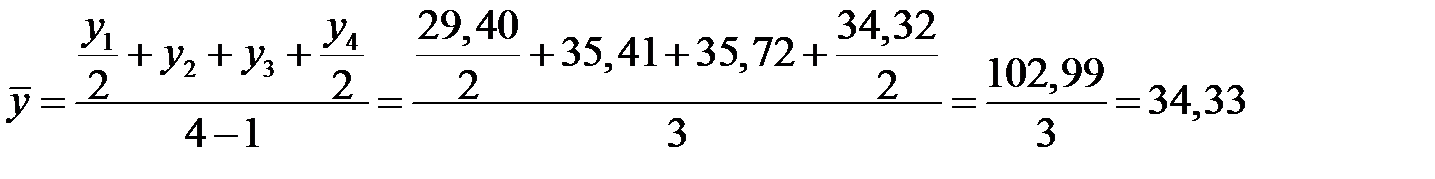 .
.
Средний уровень моментных рядов с неравностоящими уровнями определяется по формулесредней хронологической взвешенной:
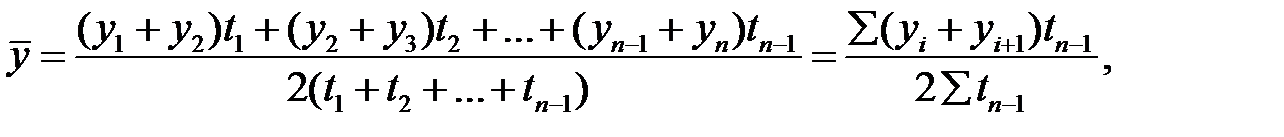 (7.4)
(7.4)
где 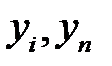 - уровни рядов динамики;
- уровни рядов динамики;
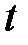 - интервал времени между смежными уровнями.
- интервал времени между смежными уровнями.
Использование в расчетах формулы (7.4) рассмотрим на следующем примере.
Таблица 7.8 - Масса остатков (запасов) дизельного топлива в фермерском хозяйстве, тонны
| Дата | 1.01.2008г. | 1.03.2008г. | 1.04.2008г. | 1.08.2008г. | 1.01.2009г. |
| Запасы дизельного топлива, т |
Нужно определить среднюю массу остатков (запасов) дизельного топлива в фермерском хозяйстве за 2008г., т:

 .
.
Обобщающий показатель скорости изменения уровней во времени – средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую:

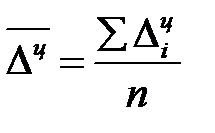 , (7.5)
, (7.5)
где 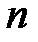 - число цепных абсолютных приростов (
- число цепных абсолютных приростов ( ) в изучаемом периоде.
) в изучаемом периоде.
Применение формулы (7.5) проиллюстрируем, используя данные таблицы 7.6 о цепных абсолютных приростах производства электроэнергии, млрд. кВт ч:
 .
.
Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост ( ). Для случая равных интервалов применим следующую формулу:
). Для случая равных интервалов применим следующую формулу:
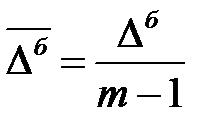 , (7.6)
, (7.6)
где  - число уровней ряда динамики в изучаемом периоде, включая базисный.
- число уровней ряда динамики в изучаемом периоде, включая базисный.
Для нашего примера, млрд. кВт ч:
 , т.е. получен тот же результат.
, т.е. получен тот же результат.
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности исчисления среднего темпа роста (снижения) применяется определяющий показатель - произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то нужно применять среднюю геометрическую.
Поскольку среднийтемп роста представляет собой средний коэффициент роста, выраженный в процентах ( ), то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
), то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
 , (7.7)
, (7.7)
где 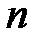 - число цепных коэффициентов роста;
- число цепных коэффициентов роста;
 - цепные коэффициенты роста;
- цепные коэффициенты роста;
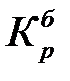 - базисный коэффициент роста за весь период.
- базисный коэффициент роста за весь период.
В нашем примере среднегодовой темп изменения производства электроэнергии с 2002 по 2007 гг.:
 .
.
 , т.е.
, т.е. 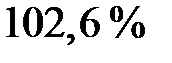 .
.
Следовательно, с 2002 по 2007 гг. производство электроэнергии в России выросло в среднем на 2,6% в год.
Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент получается как частное от деления уровня последнего периода  на уровень базисного периода
на уровень базисного периода 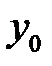 .
.
Тогда формула для расчета среднего темпа роста для равностоящих рядов динамики (по «базисному способу»):
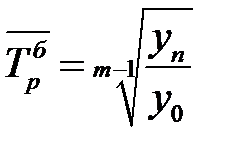 , (7.8)
, (7.8)
где 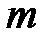 - число уровней ряда динамики в изучаемом периоде, включая базисный.
- число уровней ряда динамики в изучаемом периоде, включая базисный.
Для расчета среднего темпа роста по формуле (7.8) не нужно знать годовые темпы. Для нашего примера:
 .
.
Получен тот же результат.
Средний темп прироста (сокращения) рассчитывается на основе среднего темпа роста. Соответственно при исчислении средних коэффициентов приростаиз значений коэффициентов роста вычитается единица:
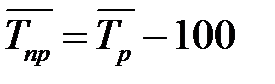 , (7.9)
, (7.9)
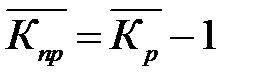 , (7.10)
, (7.10)
где  - средний темп прироста,
- средний темп прироста,
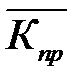 - средний коэффициент прироста.
- средний коэффициент прироста.
Рассмотрим следующий пример на исчисление показателей анализа ряда динамики.
Пример 7.4. Требуется провести анализ динамики продажи эмали ПФ за 2004 - 2008 гг. Для удобства и наглядности исходные и рассчитанные показатели представим в виде таблицы 7.10.
Таблица 7.10 - Динамика продажи эмали ПФ в одном из регионов за 2004-2008 гг. и расчет аналитических показателей динамики (данные условные)
| Годы | Эмаль ПФ, млн. усл. банок | Абсолютные приросты (снижение), млн усл. банок | Темпы роста, % | Темпы прироста, % | Абсолютное значение одного 1% прироста, млн. усл. банок | |||
| с предыдущим годом | с 2004г. | с предыдущим годом | с 2004г. | с предыдущим годом | с 2004г. | |||
| - | - | - | 100,0 | - | 0,0 | - | ||
| -85 | -85 | 90,5 | 90,5 | -9,5 | -9,5 | 8,91 | ||
| 197,9 | 179,0 | 97,9 | 79,0 | 8,06 | ||||
| 102,6 | 183,7 | 2,6 | 83,7 | 15,95 | ||||
| 100,9 | 185,3 | 0,9 | 85,3 | 16,37 | ||||
| Итого | - | - | - | - | - | - |
Таким образом, расчеты показали, что продажа эмали ПФ в 2008 г. возросла по сравнению с 2004 г.:  или
или 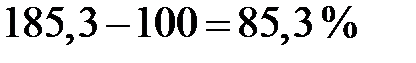 . Средняя продажа эмали ПФ за 5 лет составила:
. Средняя продажа эмали ПФ за 5 лет составила:  млн. усл. банок. Среднегодовой абсолютный прирост продажи эмали ПФ за 2004 - 2008гг. равен:
млн. усл. банок. Среднегодовой абсолютный прирост продажи эмали ПФ за 2004 - 2008гг. равен:  , или
, или 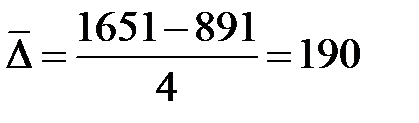 млн. усл. банок, а среднегодовой темп роста продажи эмали
млн. усл. банок, а среднегодовой темп роста продажи эмали 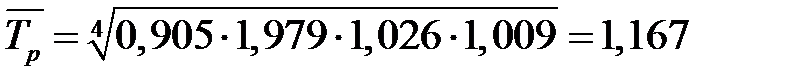 (
( ), или
), или 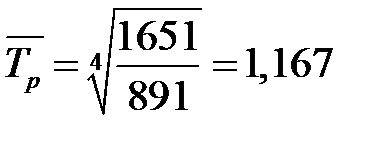 (
(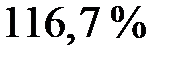 ). Среднегодовой темп прироста
). Среднегодовой темп прироста 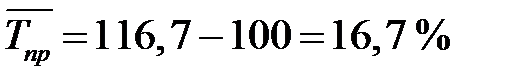 .
.
7.3 Методы анализа основной тенденции развития в рядах динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления.
В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражается уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются).
Однако часто приходится встречаться с такими рядами динамики, в которых уровни ряда претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция развития неясна.
На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайныйхарактер.
Поэтому при анализе динамики речь идет не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития.
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.
Одним из наиболее простых методов является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.
Рассмотрим применение метода укрупнения интервалов на ежемесячных данных о выпуске продукции на предприятии в 2008 г. (таблица 7.11).
Таблица 7.11 - Объем производства продукции предприятия (по месяцам) в сопоставимых ценах, млн. руб.
| Месяц | Объем производства | Месяц | Объем производства |
| Январь | 3,1 | Июль | 3,6 |
| Февраль | 3,4 | Август | 3,9 |
| Март | 3,2 | Сентябрь | 4,1 |
| Апрель | 3,3 | Октябрь | 4,0 |
| Май | 3,6 | Ноябрь | 3,9 |
| Июнь | 3,8 | Декабрь | 4,2 |
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам (таблица 7.12), т.е. укрупнить интересы,то решение задачи упрощается.
Таблица 7.12 - Объем производства продукции предприятия (по кварталам) в сопоставимых ценах, руб.
| Квартал | За квартал | В среднем за месяц |
| I | 9,7 | 3,23 |
| II | 10,7 | 3,57 |
| III | 11,6 | 3,87 |
| IV | 12,1 | 4,03 |
После укрупнения интервалов основная тенденция роста производства стала очевидной:
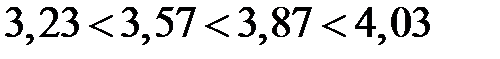 млн. руб.
млн. руб.
Выявление основной тенденции может осуществляться также методом скользящей средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем - из такого же числа уровней, но начиная со второго по счету, далее - начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок.
Расчет скользящей средней по данным об урожайности зерновых культур приведен в таблице 7.13.
Таблица 7.13 - Исходные данные и результаты расчета скользящей средней, ц/га.
| Год | Фактический уровень урожайности, ц/га | Скользящая средняя | |
| трехлетняя | пятилетняя | ||
| 16,6 | - | - | |
| 17,0 | 
| - | |
| 14,4 | 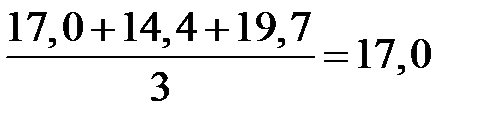
| 18,1 | |
| 19,7 | 19,0 | 19,2 | |
| 23,0 | 21,6 | 20,6 | |
| 22,1 | 22,9 | 22,6 | |
| 23,8 | 23,4 | 23,3 | |
| 24,3 | 23,7 | 23,6 | |
| 23,1 | 24,1 | - | |
| 24,9 | - | - | |

|
Сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям - на два члена в начале и конце ряда. Он меньше, чем фактический подвержен колебаниям из-за случайных причин.
Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а, следовательно, потеря информации.
Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.
Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.
Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:
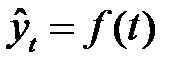 ,
,
где 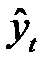 - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени  .
.
Определение теоретических (расчетных) уровней 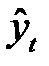 производится на основе адекватной математической модели,которая наилучшим образом отображает основную тенденцию ряда динамики.
производится на основе адекватной математической модели,которая наилучшим образом отображает основную тенденцию ряда динамики.
Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).
Например, простейшими моделями (формулами), выражающими тенденцию развития, являются:
а) линейная функция – прямая:
 ,
,
где 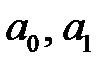 - параметры уравнения;
- параметры уравнения;
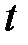 - время;
- время;
б) показательная функция:
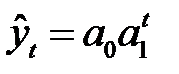 ;
;
в) степенная функция -кривая второго порядка (парабола):
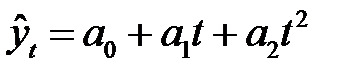 .
.
В тех случаях, когда требуется особо точное изучение тенденции развития (например, модели тренда для прогнозирования), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.
Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпиричесими уровнями:
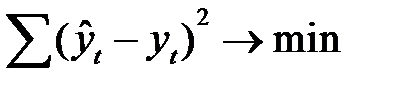 , (7.11)
, (7.11)
где 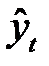 - выравненные (расчетные) уровни;
- выравненные (расчетные) уровни;
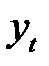 - фактические уровни.
- фактические уровни.
Параметры уравнения  , удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений.
, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений.
На основе найденного уравнения тренда вычисляются выравненные уровни.
Таким образом, выравнивание ряда динамики заключается в замене фактических уровней  , плавно изменяющимися уровнями
, плавно изменяющимися уровнями 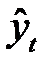 , наилучшим образом отражающими статистические данные.
, наилучшим образом отражающими статистические данные.
Выравнивание по прямойиспользуется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической профессии (или близко к ней).
Выравнивание по показательной функциииспользуется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны.
Рассмотрим «технику» выравнивания ряда динамики по прямой:  . Параметры
. Параметры  согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений,полученной путем алгебраического преобразования условия (7.11):
согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений,полученной путем алгебраического преобразования условия (7.11):
 (7.12)
(7.12)
где 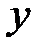 - фактические (эмпирические) уровни ряда;
- фактические (эмпирические) уровни ряда;
 - время (порядковый номер периода или момента времени).
- время (порядковый номер периода или момента времени).
Расчет параметров значительно упрощается, если за начало отсчета времени (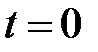 ) принять центральный интервал (момент).
) принять центральный интервал (момент).
При четном числе уровней, значения  - условного обозначения временибудут такими (это равнозначно измерению времени не в годах, а в полугодиях):
- условного обозначения временибудут такими (это равнозначно измерению времени не в годах, а в полугодиях):
| 2001г. | 2002г. | 2003г. | 2004г. | 2005г. | 2006г. |
| -5 | -3 | -1 | +1 | +3 | +5 |
При нечетном числе уровней значения устанавливаются по-другому:
| 2001г. | 2002г. | 2003г. | 2004г. | 2005г. | 2006г. | 2007г. |
| -3 | -2 | -1 | +1 | +2 | +3 |
В обоих случаях 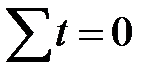 , так что система нормальных уравнений (7.12) принимает вид:
, так что система нормальных уравнений (7.12) принимает вид:
 , (7.13)
, (7.13)
Из первого уравнения системы 7.13
 , (7.14)
, (7.14)
Из второго уравнения системы 7.13 следует
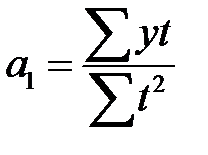 , (7.15)
, (7.15)
Рассмотрим на примере урожайности зерновых культур (см. таблицу 7.13, расчетные значения - таблица 7.14) выравнивание ряда динамики по прямой.
Для выравнивания данного ряда используем линейную трендовую модель - уравнение прямой:  . В нашем примере
. В нашем примере  - четное число. Параметры
- четное число. Параметры  искомого уравнения прямой исчислим по формулам (7.14) и (7.15).
искомого уравнения прямой исчислим по формулам (7.14) и (7.15).
Из таблицы 7.14 находим:

откуда 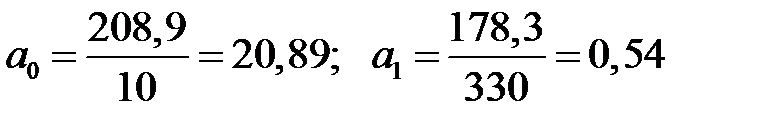 .
.
Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: 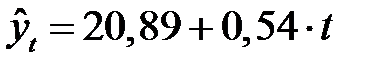 .
.
Таблица 7.14 - Выравнивание по прямой ряда динамики урожайности зерновых культур
| Год | 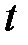
| 
| 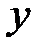
| 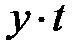
| 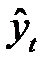
| 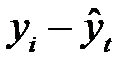
| 
|
| -9 | 16,6 | -149,4 | 16,05 | 0,55 | 0,3025 | ||
| -7 | 17,0 | -119 | 17,11 | -0,11 | 0,0121 | ||
| -5 | 14,4 | -72 | 18,19 | -3,79 | 14,3641 | ||
| -3 | 19,7 | -59,1 | 19,27 | 0,43 | 0,1849 | ||
| -1 | 23,0 | -23 | 20,35 | 2,65 | 7,0225 | ||
| +1 | 22,1 | 22,1 | 21,43 | 0,67 | 0,4489 | ||
| +3 | 23,8 | 71,4 | 22,51 | 1,29 | 1,6641 | ||
| +5 | 24,3 | 121,5 | 23,59 | 0,71 | 0,5041 | ||
| +7 | 23,1 | 161,7 | 24,67 | -1,57 | 2,4649 | ||
| +9 | 24,9 | 224,1 | 25,75 | -0,85 | 0,7225 | ||
| Итого | 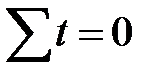
| 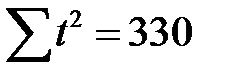
| 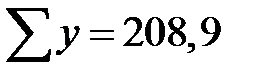
| 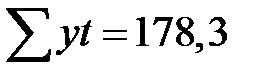
| 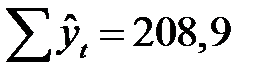
| 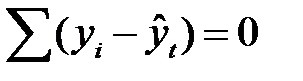
| 
|
Подставляя в данное уравнение последовательно значения 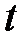 , равные -9, -7, -5, -3, -1, +1, +3, +5, +7, +9, находим выравненные уровни
, равные -9, -7, -5, -3, -1, +1, +3, +5, +7, +9, находим выравненные уровни 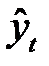 .
.
Если расчеты выполнены правильно, то 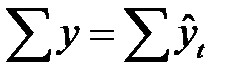 . В нашем примере
. В нашем примере  . Следовательно, значения уровней выравненного ряда найдены верно.
. Следовательно, значения уровней выравненного ряда найдены верно.
Полученное уравнение показывает, что несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 1999 по 2008 г.г. урожайность зерновых культур в среднем возрастала на  ц/га в год.
ц/га в год.






