Алгоритм метода k-средних
1. выделяют k центров a1, a2, a3, … ak,
2. выделение классов, соответствующих центрам
3. расчет новых центров для классов
a’1, a’2, ….., a’k
итерации (все аналогично для новых центров)
алгоритм останавливается, когда ничего нового не происходит.
При анализе алгоритма возникает проблема: завершится ли процесс улучшения положения центра кластера через конечное число шагов или же он может быть бесконечным. Она получила название «проблема остановки». Однако когда остановиться, сколько итераций сделать, какая точность оценивания будет при этом достигнута? Общий ответ, видимо, невозможно найти, но обычно нет ответа и для конкретных семейств распределения вероятностей. Именно поэтому мы нет оснований рекомендовать решать системы уравнений максимального правдоподобия, вместо них целесообразно использовать т.н. одношаговые оценки. Эти оценки задаются конечными формулами, но асимптотически столь же хороши (на профессиональном языке - эффективны), как и оценки максимального правдоподобия.
Двухкритериальная оптимизационная постановка кластер-анализа на основе внутрикластерного разброса и числа кластеров.
А-конечное множество
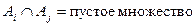
, то есть разбиение на k кластеров.
Характеристики разбиения:
1) k-число кластеров 
2) внутриклассовый разброс 
, то есть внутри кластера
, Аm-мощность множества
это невозможно решить, поэтому ее разбивают на 2 задачи более простые:
1) 
или
2) 
Кластер-анализ признаков. Измерение расстояния между признаками с помощью линейного коэффициента корреляции Пирсона и непараметрического рангового коэффициента корреляции Спирмена.
Коэффициентом корреляции Пирсона: 
Если rn = 1, то 
причем a >0
Если же rn = -1, то причем a< 0
Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.
Коэффициент ранговой корреляции Спирмена
1. Для каждого xi рассчитывают его ранг ri в вариационном ряду, построенном по выборке 
2. Для каждого yi рассчитывают его ранг qi в вариационном ряду, построенном по выборке 
3. Для набора из n пар 
вычисляют (линейный) коэффициент корреляции. Он называется коэффициентом ранговой корреляции, поскольку определяется через ранги.
Отметим, что коэффициент ранговой корреляции Спирмена остается постоянным при любом строго возрастающем преобразовании шкалы измерения результатов наблюдений.
Сокращенный вариант:
Для разбиения признаков на группы можно применять различные алгоритмы кластер-анализа. Достаточно ввести расстояние (меру близости, показатель различия) между признаками. Пусть Х и У – два признака. Различие d (X,Y) между ними можно измерять с помощью выборочных коэффициентов корреляции:
d 1(X,Y) = 1 – rn (X,Y), d 2(X,Y) = 1 – ρ n (X,Y),
где rn (X,Y) – выборочный линейный коэффициент корреляции Пирсона, ρ n (X,Y) – выборочный коэффициент ранговой корреляции Спирмена.
