A1/ A2= B1/ B2 =C1/ C2 (две прямые на плоскости либо пересекаются в одной точке либо совпадают либо параллельны)
Условия параллельности совпадает с условием коллинеарности векторов: A1/A2= B1/B2=C1/C2
Условия перпендикулярности равносильно условию перпендикулярности их направляющих векторов a1 a2 A1*A2+ B1*B2+ C1*C2
40. Разъяснить критерии взаимного расположения прямой и плоскости. Дать определение угла между прямой и плоскостью, расстояния от точки до плоскости, записать соответствующие формулы..
Взаимное расположение прямой и плоскости определяется множеством решений линейной системы

Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость. Пусть плоскость задана уравнением  , а прямая -
, а прямая -  .
.
Пусть плоскость П,задана уравнением Ax+By+Cz+D=0 и дана точка Mo(Xo;Yo; Zo). Тогда расстояние p от точки Mo до плоскости П определяется по формуле 
41. Дать определение числовой последовательности, изложить ее свойства. Перечислить виды последовательностей. и способы задания числовой последовательности.
Числовая последовательность – это числовая функция, заданная на множестве натуральных чисел.
Задать последовательность означает задать правило, по которому каждому номеру из ряда натуральных чисел соответствует одно и только одно действительное число.
Способы задания последовательности:
1) формулой общего члена
2) рекуррентной формулой
3) словесным описанием
4) графически
5) точками на числовой оси
Свойства числовых последовательностей:
1) монотонность
Последовательность называется возрастающей (убывающей), если каждый её член начиная со второго больше (меньше) предыдущего.
2) ограниченность
Последовательность называется ограниченной, если она ограничена и сверху и снизу.
Последовательность {Xn} называется ограниченной сверху (снизу), если существует число M (m) такое, что выполняется неравенство Xn≤М (Xn≥m).
42. Дать определение арифметической прогрессия и изложить ее свойства
Арифметическая прогрессия -Это последовательность, всякий член которой, начиная со второго, равен предыдущему, сложенному с постоянным числом. хn+1=хn+d
Если шаг d > 0, прогрессия является возрастающей; если d < 0, — убывающей.
Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии:
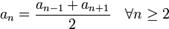 .
.
Сумма n первых членов арифметической прогрессии может быть выражена формулами

Сумма n последовательных членов арифметической прогрессии начиная с члена k:

Пример суммы арифметической прогрессии является сумма ряда натуральных чисел до n включительно:
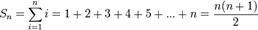
43..Дать определение геометрической прогрессия и изложить ее свойства.
Геометрическая - это последовательность, всякий член которой, начиная со второго, равен предыдущему, умноженному на постоянное число. хn+1=хn+q
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
 ,
,
Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:

Сумма n первых членов геометрической прогрессии:
 , при
, при 
 , при
, при 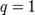
Если 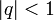 , то
, то  при
при 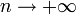 , и
, и
 при
при 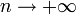 .
.
44. Дать понятие предела последовательности. Изложить критерий Коши и Сформулировать теоремы о свойствах предела последовательности.
. Конечное число а называется пределом числовой последовательности {хn}, если для любого  > 0 (сколь угодно малого) существует число N = N(
> 0 (сколь угодно малого) существует число N = N( ) такое, что |хn - а| N.
) такое, что |хn - а| N.
Обозначение: 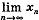 = а.
= а.
Определение 2. Числовая последовательность имеет бесконечный предел, если для любого  > 0 (сколь угодно большого) существует число N = N(
> 0 (сколь угодно большого) существует число N = N( ) такое, что | хn
) такое, что | хn  при всех n > N.
при всех n > N.
Обозначение: 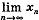 =
= 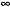 м
м
Критерий Коши:
Число а называется пределом числовой последовательности {Xn} при n стремящемся к бесконечности, если для любого сколь угодно малого положительного числа эпсилон найдётся такое натуральное число N, зависящее от эпсилон, что для всех n≥N выполняется неравенство │Xn-а│<E.
Теоремы о пределах последовательностей:
1) Если последовательности {xn} и {yn} сходятся и выполняются равенства  ,
,  , то сходятся также их сумма, разность, произведение и частное.
, то сходятся также их сумма, разность, произведение и частное.
И верны формулы:



Следствие: постоянный множитель можно выносить за знак предела.
2) Если между членами трёх последовательностей {Xn} {Yx} {Zn} выполняется неравентсво Xn≤Zn≤Yn и пределы  существуют и равны между собой, то существует и предел последовательности Zn, который равен их общему пределу.
существуют и равны между собой, то существует и предел последовательности Zn, который равен их общему пределу.
45..Дать понятие бесконечно больших и бесконечно малых последовательностей, изложить их свойства.
. Бесконечно малые и бесконечно большие последовательности:
Последовательность называется бесконечно малой, если её предел равен нулю.
Свойства бесконечно малых последовательностей:
1) сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
2) произведение ограниченной последовательности на бесконечно малую, есть бесконечно малая последовательность.
Следствие: произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
3) для того, чтобы выполнялось равенство  необходимо и достаточно, чтобы последовательность можно было представить в виде суммы постоянной величины и бесконечно малой последовательности.
необходимо и достаточно, чтобы последовательность можно было представить в виде суммы постоянной величины и бесконечно малой последовательности.
Последовательность называется бесконечно большой, если для любого числа М>0 найдется такое натуральное число N, что для всех n начиная с этого номера выполняется условие │Xn│>М.
Свойства бесконечно больших последовательностей:
1) Если {αn}бесконечно малая последовательность, то {  } бесконечно большая последовательность. Если {αn}бесконечно большая последовательность, то {
} бесконечно большая последовательность. Если {αn}бесконечно большая последовательность, то {  } бесконечно малая последовательность.
} бесконечно малая последовательность.
2) Если предел последовательности βn=∞ и все члены этой последовательности, начиная с некоторого номера, положительны, то последовательность стремится к положительной бесконечности. А если члены отрицательны, то последовательность стремится к отрицательной бесконечности.
46. Дать понятие предела функции в точке. Изложить критерий Гейне и критерий Коши. Сформулировать теоремы о свойствах пределов функций.
Предел функций в точке:
Предел в точке -числоb назв. пределом функции f в точке x=a, если для любой послед {Xk}, сходящейся к а, соответствующая последовательность значений функции {F(k)} сходится к b.
Критерий Гейне: число А называется пределом функции в точке х0, если для любой последовательности значений аргументов {xn} сходящейся к х0, соответствующая последовательность значений функций сходится к А.
Критерий Коши: число А называется пределом функции при х стремящемся к х0, если для любого эпсилон больше нуля можно указать такое положительное δ(дельта), зависящее от эпсилон, что для любого х удовлетворяющего неравенству 0<│х- х0│<δ выполняется неравенство │f(x)-А│<Е.
Теоремы о пределах:
Если существуют 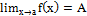 ,
,  , то существует также предел их суммы, разности, произведения и частного.
, то существует также предел их суммы, разности, произведения и частного.
Следствия:
1) постоянный множитель можно выносить за знак предела
2) предел многочлена в точке равен значению многочлена в этой точке.
3) предел дробно-рациональной функции также равен значению функции в этой точке при условии, что точка принадлежит области определения функции.
Если при вычислении предела и числитель и знаменатель имеют предел равный нулю, то нужно разделить их на двучлен х- х0 и вычислить предел, при необходимости повторить.
47 Дать понятие предела функции на бесконечности и односторонних пределов. Раскрыть суть вычисления пределов как раскрытия неопределенностей. Записать формулы замечательных пределов..
Число В называется пределом функции f(x) если для любого ε > найдеться число М>0 такое что для всех Х >М выполняеться f(x)- b < ε
Односторо́нний преде́л — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Если число А1 (число А2) есть предел функции при х, стремящемся к а так, что х принимает только значения меньшие (большие) а, то А1 (А2) называется левым (правым) пределом функции в точке а.
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:бесконечность –бесконечность, бесконечно \бесконечность,0 в нулевой степени и тд…
Первый замечательный предел:

Второй замечательный предел:
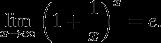
48. Определить понятия бесконечно больших и бесконечно малых функций, эквивалентности бесконечно малых функций. Записать формулы эквивалентных бесконечно малых функций.
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если  или
или  , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
Бесконечно большая функция если её придел равен +- бесокнечности.
Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→хо, т. е.
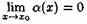 и
и 
1. Если  =А¹ 0 (АєR), то α и ß называются бесконечно малыми одного порядка.
=А¹ 0 (АєR), то α и ß называются бесконечно малыми одного порядка.
2. Если,  =0, то α називатся бесконечно малой более высокого порядка, чем ß.
=0, то α називатся бесконечно малой более высокого порядка, чем ß.
3. Если  =∞, то α называется бесконечно малой более низкого порядка, чем ß.
=∞, то α называется бесконечно малой более низкого порядка, чем ß.
4. Если  не существует, то α и ß называются несравнимыми бесконечно малыми.
не существует, то α и ß называются несравнимыми бесконечно малыми.
49. Дать определения непрерывность функции в точке. Изложить свойства функций, непрерывных в точке.
Функция yf(x непрерывна в (.)х=х0 если:
1)она в этой точке определена
2)значения предела данной функции = значению предела даной точке.
Свойства
1)если y=f(x) и y =q(x) неперывны в (.)х0. То их сумма разность, произведение, частное неперывно в точке х0.
50. Дать определение точки разрыва функции. Сформулировать условие непрерывности функции в точке. Изложить классификацию разрывов функции.
Точка в которой нарушаеться условие непрерывности называеться точкой разрыва.
Функция y=f(x) непрерыввна в х0 тогда и только тогда. если предел слева = пределу справа и = значению функции этой точки f(x0-o)=f(x0+0)=f(xo).
1)Если в точке х=х0 f(x0-o) не =f(x0+0) то х0- предел разрыва 1 рода, при этом одностороние пределы сушь и конечны
2)Ести хоть 1 из одностороних пределов бесконечен или не сушествует то х0 точка разрыва 2 рода
3)Если односториние пределы сушь, конечны и равны между собой но не раны значению функции в точке х0 то х0 точка устранимого разрыва.
51. Дать определение непрерывности функции на отрезке. Сформулировать теоремы о функциях, непрерывных на отрезке.
. Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b]
Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.
Теорема 4 (Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b).
52. Дать определение асимптоты графика функции. Назвать их виды, сформулировать условия существования...
Асимптотой называеться кривая к которой приблежаються точки на прямой, по мере удаления аргумента от начала кординат.
Виды: вертекальные горизонтальные наклонные.
1)прямая Х=а называеться вертекальной асимптотой графикаy=f(x) если хоть 1 из указаных значений х=а limf(x) и хстремиться к + или -a.
2)горизонтальная асимптота.y=f(x) при х стремиться к =или- бесконечности имеет горизонтальную асимптоту
Limf(x)=b при х стремиться к бесконечности или - бесконечности.
3)наклонная y=f(x) имеет наклонную асимптоту тогда и только тогда когда сушшь 2 конечных придела k=lim(f(x)/x) при х стремяшемся к бесконечности … lim (f(x)-kx)=b
53. Дать определение производной функции. Сформулировать и доказать основное свойство производной функции. Сформулировать правила дифференцирования и записать соответствующие формулы.
54..Раскрыть механический (физический) и геометрический смысл производной. Записать и разъяснить уравнения касательной и нормали к кривой.
Геометрический смысл производной. Если функция  имеет конечную производную в точке x 0, то в окрестности U (x 0) её можно приблизить линейной функцией
имеет конечную производную в точке x 0, то в окрестности U (x 0) её можно приблизить линейной функцией

Функция fl называется касательной к f в точке x 0. Число f '(x 0) является угловым коэффициентом или тангенсом угла наклона касательной прямой.
Скорость изменения функции
Пусть s = s (t) — закон прямолинейного движения. Тогда v (t 0) = s '(t 0) выражает мгновенную скорость движения в момент времени t 0. Вторая производная a (t 0) = s ''(t 0) выражает мгновенное ускорение в момент времени t 0.
Вообще производная функции y = f (x) в точке x 0 выражает скорость изменения функции в точке x 0, то есть скорость протекания процесса, описанного зависимостью y = f (x).
уравнение касательной 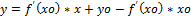 или Уравнение нормали
или Уравнение нормали 
55. Сформулировать теоремы о дифференцировании сложной и обратной функций и доказать их.
Теорема 3 (дифференцирование сложной функции). Пусть
функция x = f (t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = f (t). Тогда сложная функция y = f( f (t)) дифференцируема в точке t, причем справедлива формула
| (f (f(t))) ' = f' (x)f ' (t). Доказательство. Зададим x = f(t) отличное от нуля приращение D t. Этому приращению отвечает приращение D x = f (t+D t)-f (t) функции x = f(t). Приращению D x отвечает приращение D y = f(x+ D x)-f(x). Так как функция y = f(x) дифференцируема, то ее приращение D y представимо в виде (1): D y =f' (x)D x + a (D x) D x, где limD x® 0a (D x) = 0. Поделив данное выражение на D t ¹ 0, будем иметь: D y/ D t=f' (x)D x/ D t+ a (D x)D x/ D t. Из дифференцируемости функции x = f (t) в точке t вытекает, что limD t ® 0D x/ D t = f ' (t). Отметим, что из дифференцируемости функции x = f(t) следует, что D x® 0 при D t® 0. Следовательно, limD t® 0a (D x) =0. Таким образом, получим необходимую формулу |
Теорема 4 (производная обратной функции). Пусть функция
y = f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x. Пусть, кроме того, эта функция дифференцируема в точке x и f'(x) ¹ 0. Тогда в некоторой окрестности соответствующей точки y = f(x) определена обратная функция x = f- 1 (y), причем обратная функция дифференцируема в точке x = f- 1 (y) и для ее производной справедлива формула
(f- 1(y)) ' = 1 /f' (x).
56. Дать определение функции, заданной параметрическими уравнениями. Сформулировать теорему о дифференцировании функции, заданной параметрически, и доказать ее. Дать определение неявной функции. Сформулировать правило дифференцирования неявной функции.
57. Сформулировать и доказать теоремы Ролля, Лагранжа и Коши и их следствия.
Теорема 1. (Теорема Ролля) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b);
на концах отрезка [a, b] принимает равные значения.
Тогда существует точка c О (a, b) такая, что f'(c) = 0.
Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b).
Тогда существует точка с О (a, b) такая, что
| f(b) − f(a) = f '(c) · (b − a). |
Теорема 3. (Теорема Коши) Пусть функции f(x) и g(x)
непрерывны на отрезке [a, b];
дифференцируемы в интервале (a, b);
"x О (a, b) g'(x) ≠ 0.
Тогда существует точка c О (a, b) такая, что
|
|
58. Дать понятие о неопределенностях при вычислении пределов и назвать их виды. Сформулировать правило Лопиталя и рассказать об особенностях его применения..
59. Дать определение дифференциала функции и раскрыть его геометрический смысл. Сформулировать свойства дифференциала и записать соответствующие формулы.
Дифиринциал-линейная часть приращения функции
Свойства:1)диффиринциал постоянной =0
2)дифференциал суммы дифференциальных функций равен сумме дифиринциалов слогаемых
3)диф. Произведения 2 диф. Функций равен произведению первой на диф 2 + наоборот
4)диф частного u/v диф функций u=u(x) и v=v(x) определяеться формулой
D(u/v)=vdu-udy/v*v
60. Записать формулы, используемые в приближенных вычислениях с помощью дифференциала и. объяснить их. Привести соответствующие примеры.






