В соответствии с заданием преподавателя студент обязан произвести оптимизационные расчеты для одного из заданных видов груза.
Задача оптимизации заключается в том, чтобы выбрать такое техническое оснащение грузового фронта (число погрузочно-разгрузочных машин), при котором суммарные приведенные расходы будут минимальны. Кроме технического оснащения, определяется оптимальное количество подач вагонов на грузовой фронт.
В качестве критерия оптимизации принимаются приведенные расходы, которые включают в себя затраты, зависящие от оптимизируемых параметров (число погрузочно-разгрузочных машин – z и число подач - х). Расчеты выполняются для детерминированного или недетерминируемого режимов работы грузового фронта по указанию преподавателя.
В курсовом проекте рассматриваются следующие виды затрат:
Расходы на амортизацию и ремонт погрузочно-разгрузочных машин
где Z - число погрузочно-разгрузочных машин;
Км – стоимость погрузочно-разгрузочных машин, руб.;
А - норма годовых отчислений на амортизацию и ремонт машин;(А=0,227)
Е - коэффициент эффективности капитальных вложений (Е = 0,12);
Расходы, связанные с простоем вагонов под грузовыми операциями
Где Х - количество подач вагонов на грузовой фронт;
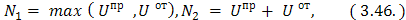
где aв-ч - стоимость одного вагоно-часа простоя, руб. (aв-ч = 29 руб/ч);
Qэ - часовая эксплуатационная производительность погрузочно-разгрузочных машин или установок, т/ч;
Расходы, связанные с простоем вагонов в ожидании подачи на грузовой фронт
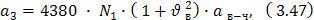
где 
в - коэффициент вариации вагонопотока на грузовой фронт (значение в равно дробной части коэффициента кн для этого груза).
Расходы, связанные с маневровыми локомотиво-часами на подачу и уборку вагонов с грузового фронта
Где tм - затраты времени на подачу и уборку вагонов с грузового фронта;
aл-ч - стоимость одного локомотива-часа маневровой работы, руб. (aл-ч = 960 руб/ч).
Расходы, связанные с простоем вагонов в ожидании выполнения с ними грузовых операций
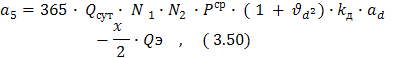
где Т - время работы грузового фронта в течение суток, ч;
Кд - коэффициент дополнительных грузовых операций, (Кд = 1,15);
Qсут - суточный объем переработки, т/сут,
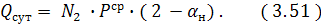
Расходы, связанные с простоем автомобилей под грузовыми операциями,
где ta - время погрузки – выгрузки одного автомобиля, ч;
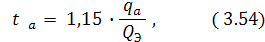
qa - средняя масса груза на автомобиле, т;
aa-ч - стоимость автомобиле-часа простоя, руб/а-ч (аа-ч =250 руб/ч);
a - коэффициент вариации, a = 0,3;
Na - число автомобилей, поступающих за сутки на грузовой фронт,
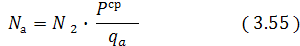
Таким образом, критерий оптимизации R(X,Z) при недетерминированном режиме работы грузового фронта с учетом вышеизложенных зависимостей имеет вид
R(X,Z)=a1*Z+a2/X*Z+a3/X+a4*X+a5/
X*Z*(T*Qэ*Z–Qсут)+a6/2*(T*Qэ*Z–Qсут) (3.56)
Если режим работы грузового фронта детерминированный, то функционал имеет более простой вид
R (X,Z) = a1*Z + a2/ X*Z + a3/X + a4*X (3.57)
Задача сводится к нахождению таких X и Z, при которых функция R(X,Z) достигает своего минимума, и решается при следующих ограничениях.
Количество подач вагонов на грузовой фронт изменяется в следующих пределах: минимальное количество подач определяется длиной фронта, максимальное количество подач – наличием маневровых ресурсов (но не более 6).
где Тм - суточные маневровые ресурсы выделенные на обслуживание данного грузового фронта, ч (Тм=3ч);
Минимальное число погрузочно-разгрузочных машин равно
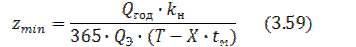
Максимальное число погрузочно–разгрузочных машин, если нет ограничений на выделяемые ресурсы, можно рассчитать по минимальной длине фронта lmin, обслуживаемого каждой машиной при беспрепятственной и безопасной работе соседних
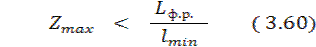
При решении оптимизационной задачи используется метод направленного перебора вариантов. Алгоритм решения состоит в следующем:
1. В качестве исходных данных принимаются минимальные значения
Х и Z.
2. Полагая Х постоянным (Х = Хmin), последовательно увеличиваем параметр Z на единицу и для каждого значения этого параметра определяем величину R (X,Z). Перебор значений производим до Zmax.Фиксируем значение минимальных приведенных расходов по строке Хmin.
3. Увеличиваем величину Х на единицу (Х = Хmin + 1) и вновь повторяем процесс перебора Z. Фиксируем минимальное значение R* по строке Х = Хmin + 1.
4. Сравниваем значение функции R*при Х и Хmin+1. Если при Х = Хmin+1, приведенные расходы меньше, переходим к следующему шагу расчетов, принимая Х = Хmin+2.
5. Повторяем расчеты, описанные в пунктах 3 и 4, до тех пор, пока приведенные расходы R* не начнут увеличиваться.
6. Значения Х и Z, при которых приведенные расходы будут минимальными R**, соответствуют искомому решению.
Описанный процесс расчетов представляется в виде табл. 3.1.
По данным табл. 3.1 студент строит график зависимости приведенных расходов от количества погрузочно-разгрузочных машин и числа подач вагонов на грузовой фронт с выделением оптимальных параметров.
Таблица 3.1.
Определение оптимальных параметров Х и Z
| Число подач Х | Количество машин Z | |||
| Z min | Z min +1 | Z min + 2 | Z max | |
| X min | R (1, 1) | R (1, 2) | R (1, 3)* | R (1, 4) |
| X min +1 | R (2, 1) | R (2, 2) | R (2, 3)* | R (2, 4) |
| X min + 2 | R (3, 1) | R (3, 2)** | R (3, 3) | |
| X min + 3 | R (4, 1) | R (4, 2)* | R (4, 3) |
