Декартовая система координат в пространстве

i j k – базис ДС

1. |i|=|j|=|k|=1

2. i┴J┴k

3. i j k –правая тройка тогда k=ixj

32.

axb= ixj=k ixk=-j jxi=-k jxk=I kxj=-I kxi=j

38.

Уравнение плоскости через точку

A(x-x0)+B(y-y0)+C(z-z0)=0

Общее уравнение

Ax+By+Cz+D=0

39.

Пересечения с осями

Ox- x=-D/A

Oy- y=-D/B

Oz- z=-D/C

ABC-наклон D-сдвиг

1. D=0 Проходит через н.к.
2. A=0 Не пересекает ох
3. А=0, Д=0 Плоскость проходит через ox
4. A=0, B=0 плоскость параллельна плоскости Oxy

40.

Уравнение плоскости в отрезках

ó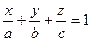

42.

Расстояние от точки до плоскости

43.

Взаимное расположение плоскостей

1. α₂||α₁ если N₁||N₂

2. α₂┴α₁ Если N₁N₂=0 A₁A₂+B₁B₂+C₁C₂=0

3. Угол между плоскостями – угол между N₁ и N₂

46.

Каноническое уравнение прямой Параметрические уравнения прямой

47.

Прямая на пересечении 2 плоскостей.

D₁ не равно D₂

48.

49.

1. l₁||l₂ если S₁||S₂ =>

2.. l₁┴l_{2 если} S₁┴S₂ =>S₁S₂=0 =>m₁m₂+n₁n₂+p₁p₂

Угол между прямыми

cosA =

Направляющие косинусы прямой – косинусы направляющего вектора.

50.

Расстояние от точки до прямой.

P – проекция M*

M*P||N

D=|M*P|=|Pr_NM₀M|=|N*M₀M|/|N|=

= =

=

51.

Угол между прямой и плоскостью

Расположение прямой и плоскости.

1. l||α => SN=>NS=0 óAm+Bn+Cp=0
2. l┴α => S||N =>

52.

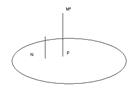Проекция точки на плоскость

α: Ax+By+Cz+D=0

l:

x=x*+At

y=y*+Bt

z=z*+Ct

подставляем в α: и получаем

Проекция точки на прямую

l:

l ┴α: m(x-x*)+n(y-y*)+p(z-z*)=0

x=x*+At

y=y*+Bt

z=z*+Ct

53.

Проекция прямой на плоскость.

I способ

1. Найти две точки на прямой А и В

2. Найти проекцию этих точек на плоскость А’ и B’

3. Провести l’ через A’B’

l:

II способ

N_b=N_axS={A1,B1,C1}

β: A1x+B1y+C1z+D1=0

x=x*+At

y=y*+Bt

z=z*+Ct

S₁=NaxNb

55, 57.

1. Каноническое уравнение

2. Параметрическое уравнение x=x₀+mt y=y₀+nt

3. Общее уравнение Ax+By+C=0

4. с угловым коэффициентом y=kx+b

58.

1. l₁||l₂ если S₁||S₂ => или k₁=k₂ или

2. l₁┴l₂ если S₁S₂=0=> A₁A₂+B₁B₂=0

59.

= tgA=k

Угол между 2 прямыми

60.

Окружность есть геометрическое место точек, равноудаленных от данной точки (центра). Если r – радиус окружности, C(a, b) – ее центр, то уравнение окружности имеет вид

|M₀M|=R

=>

61.

Эллипс есть геометрическое место точек, сумма расстояний которых до двух фиксируемых точек (фокусов) есть величина постоянная (ее обозначают через 2 a), большая расстояния между фокусами.

|F₁F₂|=2c |MF₁|+|MF₂|=2a

где a – большая, b – малая полуось эллипса, причем a, b, c связаны соотношением a ² = b ² + c ².

 

Форма эллипса характеризуется его эксцентриситетом e = .

Расстояния некоторой точки M(x, y) эллипса от фокусов (фокальные расстояния) определяются формулами r₁ = a + ex и r₁ = a – ex.

В силу определения эллипса для любой его точки r₁ + r₂ = 2 a.

Директрисами эллипса называются прямые, определяемые уравнениями x = ± .

62.

Гипербола есть геометрическое место точек, модуль разности расстояний которых от двух данных точек (фокусов) есть постоянная величина (ее обозначают через 2 а), причем эта постоянная меньше расстояния между фокусами.

Если поместить фокусы гиперболы в точках F₁ (-c, 0) и F₂(c, 0) (рис. 3.3.2), то получим каноническое уравнение гиперболы

,

где a – действительная, b – мнимая полуось.

 

Рис. 3.3.2

 

Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат.

На этих прямых лежат диагонали характеристического прямоугольника, основание которого равно 2 а, высота 2b, а центр находиться в начале координат.

Отношение называется эксцентриситетом гиперболы.

Директрисами гиперболы называются прямые, определяемые уравнениями .

Фокальные радиусы правой ветви гиперболы r₁=ex–a, r₂=ex+a. Очевидно, r₂ – r₁=2a.

Фокальные радиусы левой ветви гиперболы r₁ =- ex+a, r₂=-ex – a. Очевидно, r₁ – r₂ = 2a.

Асимптота – прямая к которой график функций приближается очень близко, при больших значениях x и y.

Гипербола имеет две асимптоты, уравнения которых .

Сопряженная гипербола

63.

Парабола есть геометрическое место точек в плоскости, равноудаленных от фокуса) и директрисы.

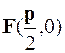Если директрисой параболы является прямая , a фокусом точка (рис. 3.3.3), то каноническое уравнение параболы имеет вид

y² = 2px.

 

Рис. 3.3.3

 

Эта парабола расположена симметрично относительно оси абсцисс. При p>0 парабола обращается в положительную сторону оси, а при p<0 – в отрицательную.

Фокальный радиус вычисляется по формуле

 

q= |MM’|=

Каноническое уравнение параболы y²=2px

А) - мнимый эллипс

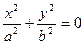- точка O(0,0,0)

б) - гипербола

- сопряженная гипербола

- 2 пересекающиеся прямые

в) y²=2px – парабола ось симметрии 0x

x²=2py - парабола ось симметрии 0y

y²=zp p=0=> ось ox p<0 нет