При определении границ систематическая погрешность оценивается по ее составляющим, называемым элементарными систематическими погрешностями. Если для части составляющих находят их оценки и эти погрешности устраняют введением поправок, то в качестве рассматриваемых элементарных погрешностей выступают погрешности определения поправок, которые также характеризуются границами. Получаемая оценка погрешности надежно характеризует неопределенность результата. При выборе закона распределения необходимо руководствоваться следующими правилами: если известна оценка границ погрешности, то ее распределение следует считать равномерным; если известна оценка СКО(среднеквадратичное отклонение), то распределение следует считать нормальным.
Применение этого правила позволяет статистически суммировать элементарные систематические погрешности и обычно приводит к осторожным и вместе с тем не слишком завышенным оценкам погрешности результата измерений.
Правила суммы случайных погрешностей.
Правила суммирования случайных погрешностей основаны на известных из теории вероятностей положениях: оценка математического ожидания результирующей погрешности определяется алгебраической суммой оценок математических ожиданий составляющих; оценка СКО суммарной погрешности определяется выражением
При суммировании m случайных погрешностей их коэффициенты корреляции образуют матрицу, которая ввиду равенства ρij = ρij является диагональной. Так как матрица коэффициентов корреляции симметрична относительно главной диагонали, на которой находятся значения ρij = 1, то формулу (9.7) можно переписать в виде
где суммирование во втором слагаемом распространяется на все те составляющие, коэффициенты корреляции которых находятся в матрице правее и выше главной диагонали. В случае суммирования нормально распределенных случайных погрешностей результирующая погрешность измерения состоит из m случайных составляющих.Зная доверительную вероятность Р и доверительный интервал Д: для каждой составляющей погрешности, можно найти оценку СКО любой из них по формуле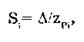 
. При суммировании составляющих с нормальным законом распределения результирующая погрешность также будет распределена нормально. Поэтому доверительный интервал суммарной погрешности с доверительной вероятностью Р может быть найден как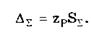 
33.
