4.1. Рівняння 
задає неявно функцію 
, на інтервалі 
, якщо для всіх 
виконується рівність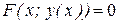 
.
Для обчислення похідної функції треба продиференціювати по 
тотожність , пам'ятаючи, що 
є функція від , а потім отримане рівняння розв’язати відносно 
.
4.2. Приклади. а) Знайти значення 
у точці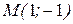 
для функції, заданої неявно рівнянням 
.
Розв’язання. Диференціюючи по обидві частини даного рівняння та вважаючи при цьому, що є функцією від , одержуємо:
,
звідки: 
.
Знаходимо значення у точці :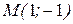
.
б) Знайти величину кута між дотичними, проведеними в точках перетину кривої 
з віссю 
. Зробити креслення.
Розв’язання. За аналогією з попереднім прикладом, знаходимо:
(*)
Точки перетину даної кривої із прямою 
знаходимо з розв’язку наступної системи:
Таких точок дві: 
і 
.
Враховуючи, що 
, 
, знаходимо згідно з (*) кутовий коефіцієнт 
дотичної до даної кривої в точці А:
.
Аналогічно знаходимо кутовий коефіцієнт 
дотичної в точці В:
.
Кут 
задовільняє рівності 
, отже 
, звідки 
126055.
Перш ніж зробити креслення, перетворимо початкове рівняння кривої 
у рівняння 
, що визначає коло із центром у точці 
та радіусом 
(рис. 4.3).
Рис. 4.3
Завдання 4. Знайти значення 
у точці 
для функцій, заданих неявно.
| 1. | 5 x 2 + 3 xy – 2 y 2 + 2 = 0 | M (0; 1) |
| 2. | x 3 – 2 x 2 + y 2 = 0 | M (1; 1) |
| 3. | x 2 + xy + y 2 = 7 | M (–1; –2) |
| 4. | 2 x 3 – xy + y – 2 = 0 | M (1; 5) |
| 5. | x 3 + y 3 – 3 xy + 1 = 0 | M (–2;1) |
| 6. | 3 x 2 – xy + y – 3 = 0 | M (1; –2) |
| 7. | x 2 + 2 y 2 + 6 x – 4 y – 13 = 0 | M (1; –1) |
| 8. | 3 x 2 – 5 y2 – 6 x – 20 y + 25 = 0 | M (2; 1) |
| 9. | 4 x 2 + y 2 + 8 x – 4 y + 3 = 0 | M (0; 1) |
| 10. | x 3 – 2 x 2 y 2 + 5 x + y – 5 = 0 | M (1; 1) |
| 11. | 2 x 2 – 9 y 2 + 4 x + 18 y + 11 = 0 | M (2; –1) |
| 12. | x 3 – xy + y + 7 = 0 | M (–1; –3) |
| 13. | x 2 + y 2 – 4 x – 10 y + 19 = 0 | M (3; 2) |
| 14. | x 4 – y 2 – y – 1 = 0 | M (1; 0) |
| 15. | x 3 + 2 xy 2 + y + 11 = 0 | M (–1; –2) |
| 16. | x 3 + x 2 y + y 2 –13 = 0 | M (1; 3) |
| 17. | x 3 + 5 xy + y 3 – 7 = 0 | M (1; 1) |
| 18. | x 2 + 5 xy + y 2 – 2 x + y – 6 = 0 | M (1; 1) |
| 19. | 3 x 2 – xy + y 3 – x = 0 | M (0; 2) |
| 20. | x 6 + y 6 – 2 xy = 0 | M (1; 1) |
| 21. | x 2 + x 2 y – y 2 – y = 0 | M (1; 1) |
| 22. | x 4 – 6 x 2 y 2 + 9 y 2 – 5 x 2 + 15 y 2 + 4 = 0 | M (2; 1) |
| 23. | 7 x 2 + xy – y 3 + 3 = 0 | M (1; –2) |
| 24. | x 2 y 2 + xy + x 2 – 7 = 0 | M (1; 2) |
| 25. | 2 x 5 + y 5 – 2 xy + 26 = 0 | M (1; –2) |
| 26. | x 5 + y 5 – 2 xy = 0 | M (1; 1) |
| 27. | 3 x 2 – xy + y 2 + x – 34 = 0 | M (–2; 4) |
| 28. | x 2 + 2 xy 2 + 3 y 4 –6 = 0 | M (1; –1) |
| 29. | x 2 – x 2 y + y 2 = 13 | M (–1; –3) |
| 30. | x 2 y 2 – 4 y 3 – x = 4 | M (0; –1) |
Завдання 5. Знайти величину кута між дотичними, проведеними в точках перетину кривої 
з віссю . Зробити креслення.
| 1. | x 2+ y 2 + 2x + 2y –3 = 0. | 2. | x 2 + y 2 – 2x + 4y –3 = 0. |
| 3. | x 2 + y 2 + 10x + 9 = 0. | 4. | x 2 + y 2 + 6x + 6y + 8 = 0. |
| 5. | x 2 + y 2 + 4x + 2y + 3 = 0. | 6. | x 2 + y 2 + 4x – 2y – 4 = 0. |
| 7. | x 2 + y 2 + 6x – 6y + 8 = 0. | 8. | x 2 + y 2 + 4x – 4y + 3 = 0. |
| 9. | x 2 + y 2 + 6x + 2y + 1 = 0. | 10. | x 2 + 6x + y 2 – 2y + 1 = 0. |
| 11. | x 2 + 10x+ y 2 – 6y +16 = 0. | 12. | x 2 + y 2 + 14x + 40 = 0. |
| 13. | x 2 + y 2 – 6x – 2y + 6 = 0. | 14. | x 2 + y 2 – 10 x+ 9 = 0. |
| 15. | x 2 + y 2 + 10x + 6y + 16 = 0. | 16. | x 2 + y 2 – 4x + 2y + 3 = 0. |
| 17. | x 2 + y 2 – 2x + 4y – 20 = 0. | 18. | x 2 + 6x + y 2 – 2y + 6 = 0. |
| 19. | x 2 + y 2 – 4y – 4 = 0. | 20. | x 2 – 6x + y 2 – 6y + 8 = 0. |
| 21. | x 2 + y 2 – 14x + 40 = 0. | 22. | x 2 + y 2 – 2x + 6y – 6 = 0. |
| 23. | x 2 + y 2 – 6x + 6y + 8 = 0. | 24. | x 2 + y 2 – 6x + 2y + 1 = 0. |
| 25. | x 2 + 4x + y 2 – 2y + 3 = 0. | 26. | x 2 + 4x + y 2 + 2y – 4 = 0. |
| 27. | x 2 + y 2 + 4x – 4 = 0. | 28. | x 2 + y 2 + 2x – 2y – 4 = 0. |
| 29. | x 2 + 4x + y 2 – 2y – 3 = 0. | 30. | x 2 + y 2 + 2x + 4y – 4 = 0. |
ПРАВИЛО ЛОПІТАЛЯ
5.1. При розкритті невизначеностей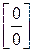 
, 
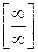крім класичних методів обчислення границь, у багатьох випадках можна користуватися правилом Лопіталя: якщо 
або 
й існує границя відношення їх похідних 
, то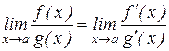 
.
Це правило справедливе й у випадку, коли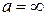 
.
Приклад 1. Застосовуючи правило Лопіталя, знайти границі:
а) 
; б) 
; в) 
.
Розв’язання. Переконавшись, що має місце випадок 
або 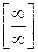, застосовуємо правило Лопіталя.
а) 
,
б) 
.
Тут двічі було застосовано правило Лопіталя й використана перша чудова границя.
в) 
.
5.2. При розкритті невизначеностей 
для застосування правила Лопіталя, початковий вираз необхідно перетворити до невизначеностей виду або 
шляхом алгебраїчних перетворень.
Приклад 2. Знайти границі: а) 
; б) 
.
Розв’язання: а) Маємо невизначеність 
. Наведемо цю невизначеність до невизначеності , а потім застосуємо правило Лопіталя:
.
б) Маємо невизначеність 
. Перетворимо початковий вираз до невизначеності , після чого застосуємо правило Лопіталя: 
.
5.3. При розкритті невизначеностей 
, 
, 
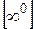рекомендується знайти попередньо границю логарифма шуканої функції.
Приклад 3. Обчислити 
.
Розв’язання. Маємо невизначеність 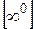. Введемо позначення 
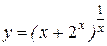, тоді 
. 
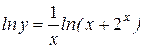. Одержали , застосовуємо правило Лопіталя: 
. Тому що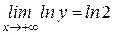 
. Отже 
.
Завдання 6. Обчислити границі, використовуючи правило Лопіталя.
| 1. | а)  ,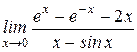
| б)  .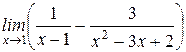
|
| 2. | а)  ,
| б)  .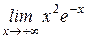
|
| 3. | а)  ,
| б)  .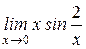
|
| 4. | а)  ,
| б)  .
|
| 5. | а)  ,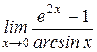
| б)  .
|
| 6. | а)  ,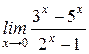
| б)  .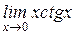
|
| 7. | а)  ,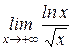
| б)  .
|
| 8. | а)  ,
| б)  .
|
| 9. | а)  ,
| б)  .
|
| 10. | а)  ,
| б)  .
|
| 11. | а)  ,
| б)  .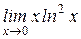
|
| 12. | а)  ,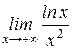
| б)  .
|
| 13. | а)  ,
| б)  .
|
| 14. | а)  ,
| б)  .
|
| 15. | а)  ,
| б)  .
|
| 16. | а)  ,
| б)  .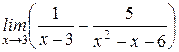
|
| 17. | а)  ,
| б)  .
|
| 18. | а)  ,
| б)  .
|
| 19. | а)  ,
| б)  .
|
| 20. | а)  ,
| б)  .
|
| 21. | а)  ,
| б)  .
|
| 22. | а)  ,
| б)  .
|
| 23. | а)  ,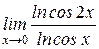
| б)  .
|
| 24. | а)  ,
| б)  .
|
| 25. | а)  ,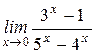
| б)  .
|
| 26. | а)  ,
| б)  .
|
| 27. | а)  ,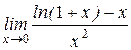
| б)  .
|
| 28. | а)  ,
| б)  .
|
| 29. | а)  ,
| б)  .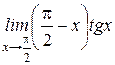
|
| 30. | а)  ,
| б)  .
|
СПИСОК ЛІТЕРАТУРИ
| 1. | Берман Г.Е. Сборник задач по курсу математического анализа. – М.: Наука, 1977. – 456 с. | |
| 2. | Бронштейн И.Н., Семендяев К.А. Сравочник по математике для инженеров и студентов ВУЗов. – М.: Наука, 1986. – 544 с. | |
| 3. | Бубняк Т.І. Вища математика: Навчальний посібник. – Львів: «Новий світ-2000», 2004. – 434 с. | |
| 4. | Вища математика: Підручник: У 2 кн. – 2-ге вид., перероб. і доп. – К.: Либідь, 2003. – Кн. 1. Основні розділи / Г.Й. Призва, В.В. Плахотник, Л.Д. Гординський та ін.; за ред. Г.Л. Кулініча. – 400 с. | |
| 5. | Вища математика. Основні означення, приклади і задачі. Ч. 1, 2. – К.: Либідь, 1992. – 349 с. | |
| 6. | Глушков П.М., Шунда Н.М. Диференціальне числення фукнцій однієї змінної. – К.: Вища шк., 1991. – 343 с. | |
| 7. | Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1,2 – М.: Высш. шк., 1980. – 320 с. | |
| 8. | Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966. – 269 с. | |
| 9. | Каплан И.А. Практические занятия по высшей математике. – Харьков.: Изд-во ХГУ, 1967. – 236 с. | |
| 10. | Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1969. – 123 с. | |
| 11. | Мантуров О.В., Матвеев Н.М. Курс высшей математики. – М.: Высш. шк., 1986. – 296 с. | |
| 12. | Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1969. – 350 с. | |
| 13. | Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М. Высшая математика. Ч.1, 2. – К.: Вища шк., 1987, 1989. – 551 с. | |
| 14. | Пискунов Н.С. Дифференциальное и интегральное исчисление, т.1, 2. – М.: Наука, 1982. – 294 с. | |
| 15. | Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики. – М.: Высш. шк., 1987. – 320 с. |
