1.1. Похідною функції  називається границя відношення приросту цієї функції до відповідного приросту аргументу
називається границя відношення приросту цієї функції до відповідного приросту аргументу  , коли приріст аргументу прямує до нуля:
, коли приріст аргументу прямує до нуля:
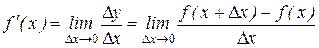 .
.
Якщо ця границя кінцева, то похідна існує, й функція  називається диференційованою в точці
називається диференційованою в точці  . Похідна позначається також
. Похідна позначається також  або
або  . Операція відшукання похідної називається диференціюванням функції.
. Операція відшукання похідної називається диференціюванням функції.
1.2. Правила диференціювання функцій. Нехай  – стала,
– стала,  ,
,  – функції, що мають похідні.
– функції, що мають похідні.
1.  ; ;
| ||
2.  ; ;
|  ; ;
| |
3.  ; ;
| 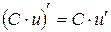 ; ;
|  . .
|
4.  ; ;
|  ; ;
| 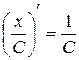 . .
|
5. Правило диференціювання складної функції. Якщо функція  диференційована по
диференційована по  , а функція
, а функція  – по
– по  , то складна функція
, то складна функція 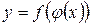 має похідну
має похідну  чи
чи  .
.
1.3. Таблиця похідних функцій:
| Похідні основних елементарних функцій | Похідні складних елементарних
функцій, 
|
1. 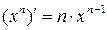 . .
| 1а.  . .
|
2.  . .
| 2а.  . .
|
3.  . .
| 3а. 
|
4.  . .
| 4а. 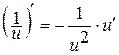 . .
|
5. 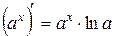 . .
| 5а.  . .
|
6.  . .
| 6а.  . .
|
7.  . .
| 7а.  . .
|
8.  . .
| 8а.  . .
|
9.  . .
| 9а.  . .
|
10.  . .
| 10а. 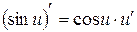 . .
|
11.  . .
| 11а.  . .
|
12.  . .
| 12а. 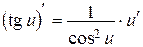 . .
|
13.  . .
| 13а.  . .
|
14.  . .
| 14а.  . .
|
15.  . .
| 15а.  . .
|
16.  . .
| 16а.  . .
|
17.  . .
| 17а.  . .
|
1.4. Похідні вищих порядків. Похідною другого порядку (другою похідною) від функції  називається похідна від її похідної, тобто
називається похідна від її похідної, тобто
 .
.
Другу похідну також позначають  або
або  . Похідна від похідної другого порядку називається похідною третього порядку і так далі. Похідну
. Похідна від похідної другого порядку називається похідною третього порядку і так далі. Похідну  -го порядку позначають
-го порядку позначають  або
або  .
.
1.5. Приклади. Використовуючи правила диференціювання й таблицю похідних, знайдемо похідні наступних функцій:
1)  ; ;
| 2) 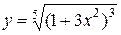 ; ;
| 3)  ; ;
|
4)  ; ;
| 5) 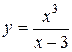 ; ;
| 6)  ; ;
|
7)  . .
|
Розв’язання
1) Перепишемо задану функцію, надавши доданки у вигляді степеня:  . Тоді застосувавши формулу 2 п. 1.2 правил диференціювання, а також формулу 1а п. 1.3:
. Тоді застосувавши формулу 2 п. 1.2 правил диференціювання, а також формулу 1а п. 1.3:
 .
.
2) Записуємо задану функцію у вигляді степеня:  та обчислюємо похідну, застосувавши формулу 1а п. 1.3:
та обчислюємо похідну, застосувавши формулу 1а п. 1.3:
 .
.
3) Застосувавши формулу 3 п. 1.2 правил диференціювання, а також формулу 1 та формулу 14 п 1.3, знаходимо:
 .
.
4) Диференціюючи функцію  як складну, знаходимо похідну:
як складну, знаходимо похідну:

5) Відповідно до формули 4 п. 1.2 одержуємо:
 .
.
6) За аналогією із прикладом 3 знаходимо:

7) Так як дана функція – показникова, то відповідно до формули 5а п.1.3:

1.6. Степенево-показникова функція. Виведемо формулу для похідної степенево-показникової функції  , враховуючи, що
, враховуючи, що  та
та  диференційовані функції та
диференційовані функції та 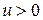 .
.
Логарифмуючи рівність  і диференціюючи обидві частини отриманої рівності
і диференціюючи обидві частини отриманої рівності  , знаходимо:
, знаходимо:  . Отже,
. Отже,  . Таким чином, одержуємо
. Таким чином, одержуємо 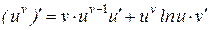 .
.
Наприклад, знайти похідну функції  , де
, де  .
.
Прологарифмуємо задану функцію: 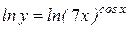 . Використовуючи основні властивості логарифмів (
. Використовуючи основні властивості логарифмів (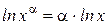 ,
,  ,
,  ), отримаємо:
), отримаємо:  .
.
Продиференціюємо отриману неявну функцію:  . Відповідно до формули 9а п.1.3 (для лівої частини) та до формули 3 п.1.2 (для правої частини), отримуємо:
. Відповідно до формули 9а п.1.3 (для лівої частини) та до формули 3 п.1.2 (для правої частини), отримуємо: 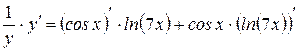 ;
;  ;
;  . Далі:
. Далі: 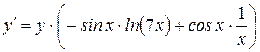 . Підставивши задану спочатку функцію в останній вираз, отримаємо:
. Підставивши задану спочатку функцію в останній вираз, отримаємо:  .
.
Завдання 1. Знайти перші похідні функцій. У завданнях а) і б) додатково знайти другі похідні.
| 1. | а) у =  ; е) у = x2 × cos7x;
б) у = ; е) у = x2 × cos7x;
б) у =  ; ж) у = ; ж) у =  ;
в) у = (х + 2) × ;
в) у = (х + 2) ×  ; з) у = ln 5 sin x;
г) у = ; з) у = ln 5 sin x;
г) у =  + 8x; и) у = arcsin e 4x;
д) у = + 8x; и) у = arcsin e 4x;
д) у = 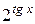 + 3 + 3  ; к) у = ; к) у =  . .
|
| 2. | а) у =  ; е) у = х × arctg 3x;
б) у = ; е) у = х × arctg 3x;
б) у =  ; ж) у = ; ж) у =  ;
в) у = ;
в) у = 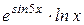 ; з) у = 3 sin2 x × cos 2x;
г) у = ln sin (2x + 5); и) у = ; з) у = 3 sin2 x × cos 2x;
г) у = ln sin (2x + 5); и) у =  ;
д) у = ;
д) у = 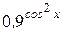 ; к) у = ; к) у =  . .
|
| 3. | а) у =  ; е) у = ; е) у =  ;
б) у = ;
б) у =  – – 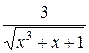 ; ж) у = ; ж) у =  ;
в) у = (ln x +1)2 × cos 2x; з) у = sin2 2x+ cos x;
г) у = arcsin ;
в) у = (ln x +1)2 × cos 2x; з) у = sin2 2x+ cos x;
г) у = arcsin  ; и) у = ln tg 5x;
д) у = 5 tg x + 3 ; и) у = ln tg 5x;
д) у = 5 tg x + 3  ; к) у = ; к) у =  . .
|
| 4. | а) у =  ; е) у = ; е) у =  ;
б) у = ;
б) у =  + 4x × ln x; ж) у = (х 2 +1) × arctg 4x;
в) у =arcsin(3x2 + 2); з) у = (2х + 5) × + 4x × ln x; ж) у = (х 2 +1) × arctg 4x;
в) у =arcsin(3x2 + 2); з) у = (2х + 5) ×  ;
г) у = ;
г) у =  ; и) у = ln ; и) у = ln  ;
д) у = ;
д) у =  ; к) у = ; к) у = 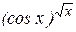 . .
|
| 5. | а) у =  ; е) у = е х × cos x;
б) у = ; е) у = е х × cos x;
б) у =  ; ж) у = 3 х 2 × ln x 3;
в) у = arctg ; ж) у = 3 х 2 × ln x 3;
в) у = arctg  ; з) у = ; з) у =  ;
г) у = х × arccos ;
г) у = х × arccos  ; и) у = (2х + 2 cos x) × е –х;
д) у = ; и) у = (2х + 2 cos x) × е –х;
д) у =  ; к) у = (sin 2x)cos x. ; к) у = (sin 2x)cos x.
|
| 6. | а) у =  ; е) у = е ; е) у = е 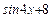 ;
б) у = ;
б) у =  ; ж) у = ; ж) у =  – ln 4x;
в) у = – ln 4x;
в) у =  ; з) у = ; з) у =  ;
г) у = ;
г) у =  + 8x + 7; и) у = cos 100 x + sin 100x;
д) у = (х + х 2) х; к) у = + 8x + 7; и) у = cos 100 x + sin 100x;
д) у = (х + х 2) х; к) у =  . .
|
| 7. | а) у =  ; е) у = (1 – х2 ) × cos 2x;
б) у = ; е) у = (1 – х2 ) × cos 2x;
б) у =  ; ж) у = ; ж) у =  ;
в) у = ;
в) у =  ; з) у = е –х × sin 2x;
г) у = arctg(ln x) +ln(sinx); и) у = ln 5(x 2 – 1);
д) у = 2 × cos(4x+x2); к) у = ; з) у = е –х × sin 2x;
г) у = arctg(ln x) +ln(sinx); и) у = ln 5(x 2 – 1);
д) у = 2 × cos(4x+x2); к) у =  . .
|
| 8. | а) у =  ; е) у = sin 4 х + cos 4 x;
б) у = ; е) у = sin 4 х + cos 4 x;
б) у =  ; ж) у = ln ; ж) у = ln  ;
в) у = 3х × arcsin 2x; з) у = (х2 + 2х + 2) × е -х;
г) у = ;
в) у = 3х × arcsin 2x; з) у = (х2 + 2х + 2) × е -х;
г) у =  + +  ; и) у = sin(x+ 6) – x × cos 4x;
д) у = 3 ctg x + 8 ; и) у = sin(x+ 6) – x × cos 4x;
д) у = 3 ctg x + 8  ; к) у = ; к) у =  . .
|
| 9. | a) у = 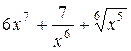 ; е) у = ln(x 2 + 5);
б) у = ; е) у = ln(x 2 + 5);
б) у =  ; ж) у = х 5 × е –х;
в) у = ; ж) у = х 5 × е –х;
в) у =  ; з) у = arctg ; з) у = arctg  ;
г) у = ln 3 sin (3x + 3); и) у = ;
г) у = ln 3 sin (3x + 3); и) у =  ;
д) у = ;
д) у =  ; к) у = ; к) у =  . .
|
| 10. | a) у =  ; е) у = 8х × ; е) у = 8х ×  ;
б) у = ;
б) у =  ; ж) у = (3х +1) 5 × cos3x;
в) у = ; ж) у = (3х +1) 5 × cos3x;
в) у =  ; з) у = ; з) у =  ;
г) у = ln (2x3 +3x2 ); и) у = arctg 2 e x;
д) у = ;
г) у = ln (2x3 +3x2 ); и) у = arctg 2 e x;
д) у =  ; к) у = ; к) у =  . .
|
| 11. | a) у =  ; е) у = cos (10x+x3);
б) у = (5х + х 3) × ln x 2; ж) у = ; е) у = cos (10x+x3);
б) у = (5х + х 3) × ln x 2; ж) у =  ;
в) у = ;
в) у =  +2sin 4x + 4; з) у = +2sin 4x + 4; з) у =  ;
г) у = arccos ;
г) у = arccos  ; и) у = ln(4+sin4x);
д) у = 0,7 arctg х; к) у = ; и) у = ln(4+sin4x);
д) у = 0,7 arctg х; к) у =  . .
|
| 12. | а) у = 3х 5 –  ; е) у = ln tg(2x+1);
б) у = ; е) у = ln tg(2x+1);
б) у =  ; ж) у = ; ж) у =  ;
в) у = (х + 1)2 × cos5x; з) у = 23х + 7х 7 + ;
в) у = (х + 1)2 × cos5x; з) у = 23х + 7х 7 +  ;
г) у = arctg(е2x + 3); и) у = ;
г) у = arctg(е2x + 3); и) у = 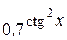 ;
д) у = ;
д) у =  ; к) у = х arcsin x. ; к) у = х arcsin x.
|
| 13. | a) у =  ; е) у =(3х + 2) × sin 3x;
б) у = ; е) у =(3х + 2) × sin 3x;
б) у =  ; ж) у = ln 2 tg 2x ; ж) у = ln 2 tg 2x  ;
в) у = ;
в) у = 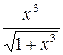 ; з) у = ; з) у =  ;
г) у = х × arccos x – ;
г) у = х × arccos x –  ; и) у = arcsin(e 7x );
д) у = ; и) у = arcsin(e 7x );
д) у =  ; к) у = (sin2x) x. ; к) у = (sin2x) x.
|
| 14. | а) у = 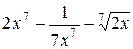 ; е) у = arctg x 2 + 7x6 + 2 ;
б) у = ; е) у = arctg x 2 + 7x6 + 2 ;
б) у =  ; ж) у = ; ж) у =  ;
в) у = (3 – sin 2 x) 3; з) у = х 2 × ln(x 2 + 1);
г) у = ;
в) у = (3 – sin 2 x) 3; з) у = х 2 × ln(x 2 + 1);
г) у =  + sin (3x + 9); и) у = + sin (3x + 9); и) у = 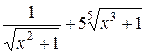 ;
д) у = ;
д) у =  + 3; к) у = (sin x) tg x. + 3; к) у = (sin x) tg x.
|
| 15. | a) у =  ; е) у = е х× sin 2x;
б) у = ; е) у = е х× sin 2x;
б) у =  ; ж) у = arctg ; ж) у = arctg  ;
в) у = (5 + х 3) 2 × е –х; з) у = ;
в) у = (5 + х 3) 2 × е –х; з) у =  ;
г) у = ;
г) у =  ; и) у = cos (3x );
д) у = ; и) у = cos (3x );
д) у =  ; к) у = ; к) у = 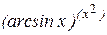 . .
|
| 16. | a) у =  ; е) у =(х 2 + 6) × ln 3x;
б) у = ; е) у =(х 2 + 6) × ln 3x;
б) у = 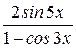 ; ж) у = ; ж) у =  + +  ;
в) у = ;
в) у =  ; з) у = е 3х × cos 3x;
г) у = 2tg 3(x 3 + 2); и) у = arctg 2 ; з) у = е 3х × cos 3x;
г) у = 2tg 3(x 3 + 2); и) у = arctg 2  ;
д) у = 2 sin 3x; к) у = ;
д) у = 2 sin 3x; к) у =  . .
|
| 17. | a) у =  ; е) у = sin 26x + 3x2;
б) у = ln ctg 3 x; ж) у = ; е) у = sin 26x + 3x2;
б) у = ln ctg 3 x; ж) у =  ;
в) у = ;
в) у = 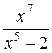 ; з) у = ; з) у = 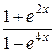 ;
г) у = arctg(tg 2 x + 2); и) у = ;
г) у = arctg(tg 2 x + 2); и) у =  ;
д) у = ;
д) у =  + 7 + 7  ; к) у = ; к) у = 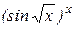 . .
|
| 18. | а) у = 3x5 – 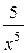 + +  ; е) y = ; е) y = 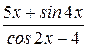 ;
б) y = arcsin (3x3 + 4); ж) y = ln cos(5x 3 + 4);
в) y = (x+ 8) × arctg 4x3 ; з) y = (ctg 3x + 1)5;
г) y = ;
б) y = arcsin (3x3 + 4); ж) y = ln cos(5x 3 + 4);
в) y = (x+ 8) × arctg 4x3 ; з) y = (ctg 3x + 1)5;
г) y = 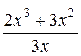 ; и) y = 5 ; и) y = 5  ;
д) y = 4x × (1 – 3ln x); к) y = (cos x) ;
д) y = 4x × (1 – 3ln x); к) y = (cos x) 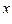 . .
|
| 19. | a) у = x7 –  ; е) у = ; е) у = 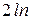 ctg ctg  ;
б) у = ;
б) у =  arctg arctg 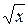 ; ж) у = ; ж) у =  ;
в) у = ;
в) у =  ; з) у = arcsin (e –4x);
г) у = ; з) у = arcsin (e –4x);
г) у =  ; и) у = ; и) у =  + 3 + 3  ;
д) у = ln 2 sin3x; к) у = ;
д) у = ln 2 sin3x; к) у =  . .
|
| 20. | a) у =  ; е) у = ; е) у =  + +  ;
б) у = ;
б) у = 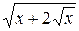 ; ж) у = ln 2 arctg x;
в) у = ; ж) у = ln 2 arctg x;
в) у = 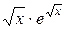 + 5 + 5  ; з) у = ; з) у =  (tg (tg  );
г) у = arctg(7sin3x); и) у = );
г) у = arctg(7sin3x); и) у =  ;
д) у = ;
д) у =  ; к) у = ; к) у =  . .
|
| 21. | a) у =  ; е) у = ; е) у =  ;
б) у = ;
б) у =  ; ж) у =3 tg 6 x + 7;
в) у = ; ж) у =3 tg 6 x + 7;
в) у = 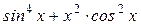 ; з) у = 4х × arctg (2x+ 9);
г) у = ; з) у = 4х × arctg (2x+ 9);
г) у =  ; и) у = ; и) у =  ;
д) у = ;
д) у =  ; к) у = ; к) у =  . .
|
| 22. | а)у =  ; е) у = sin x × cos(7x+ 5);
б) у = ; е) у = sin x × cos(7x+ 5);
б) у =  ; ж) у = (е cos x + 3)2;
в) у = х 2 × ; ж) у = (е cos x + 3)2;
в) у = х 2 ×  ; з) у = ln sin (3x + 5);
г) у =arctg ; з) у = ln sin (3x + 5);
г) у =arctg  ; и) у = ; и) у =  ;
д) у = ;
д) у =  ; к) у = (х 3) ln х. ; к) у = (х 3) ln х.
|
| 23. | a) y =  ; е) у = tg (x 2 +cos x);
б) у = ; е) у = tg (x 2 +cos x);
б) у =  ; ж) у = ; ж) у =  ;
в) у = ;
в) у =  arctg x; з) у = arctg x; з) у =  ;
г) у = ;
г) у =  ; и) у = ; и) у =  ;
д) у = ;
д) у =  ; к) у = ; к) у =  arctg x . arctg x .
|
| 24. | a) у =  ; е) у = ; е) у =  + 5 + 5  ;
б) у = tg x + ;
б) у = tg x +  tg 3 x + tg 3 x +  tg 5 x; ж) у = ln 2 sin x;
в) у = х 3 × (х – 5 cos x)2 з) у = arccos tg 5 x; ж) у = ln 2 sin x;
в) у = х 3 × (х – 5 cos x)2 з) у = arccos  ;
г) у = ;
г) у = 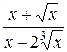 ; и) у = (1 + 9х) × ; и) у = (1 + 9х) ×  ;
д) у = 5 ;
д) у = 5  ; к) у = (1 + х)cos x. ; к) у = (1 + х)cos x.
|
| 25. | a) у =  ; е) у = ln(2x – 3);
б) у = ; е) у = ln(2x – 3);
б) у =  × x2; ж) у = × x2; ж) у =  ;
в) у = arctg(x 2+e3x); з) у = (2х3 + 5)4 × х 3;
г) у = ln tg (5x+1); и) у = sin 5x+cos 3x 3;
д) у = 3ln3x; к) у = ;
в) у = arctg(x 2+e3x); з) у = (2х3 + 5)4 × х 3;
г) у = ln tg (5x+1); и) у = sin 5x+cos 3x 3;
д) у = 3ln3x; к) у = 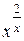 . .
|
| 26. | a) y =  ; е) у = сos2x –2ln cosx;
б) у = arctg ; е) у = сos2x –2ln cosx;
б) у = arctg  ; ж) у = ; ж) у =  ;
в) у = ;
в) у =  ; з) у = ; з) у =  ;
г) у = х2 × ctg2x; и) у = ;
г) у = х2 × ctg2x; и) у =  ;
д) у = cos25x + 7x; к) у = (cos x)sin x. ;
д) у = cos25x + 7x; к) у = (cos x)sin x.
|
| 27. | а) y =  ; е) у = ; е) у =  ;
б) у = tg (x 2 +3); ж) у = ;
б) у = tg (x 2 +3); ж) у =  ;
в) у = ;
в) у =  ; з) у = ; з) у =  ;
г) у = ln tg ;
г) у = ln tg  ; и) у = ; и) у =  ;
д) у = х 2 × arcsin (9x + 2); к) у = ;
д) у = х 2 × arcsin (9x + 2); к) у =  . .
|
| 28. | а) у = 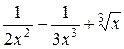 ; е) у = arctg ; е) у = arctg  ;
б) у = ;
б) у =  ; ж) у = ; ж) у =  ;
в) у = (х + 5) 7 × sin3x; з) у = (х+1)× arccos (x 2 +1);
г) у = ;
в) у = (х + 5) 7 × sin3x; з) у = (х+1)× arccos (x 2 +1);
г) у =  ; и) у = ; и) у =  ;
д) у = 52ctg x; к) у = (tg x)х. ;
д) у = 52ctg x; к) у = (tg x)х.
|
| 29. | а) у =  ; е) у = е ctg 3 x;
б) у = ; е) у = е ctg 3 x;
б) у =  × arccos × arccos  ; ж) у = ; ж) у =  ;
в) у = ;
в) у =  ; з) у = ; з) у =  ;
г) у = arctg 2 x + 6x2; и) у = (х 3 + х 2) × е –х;
д) у = ;
г) у = arctg 2 x + 6x2; и) у = (х 3 + х 2) × е –х;
д) у =  + 7 + 7  ; к) у = ; к) у =  . .
|
| 30. | а) у =  ; е) у = ; е) у =  ;
б) у = 3х × sin 5x + 8; ж) у =х× (cos ln x + sin lnx);
в) у = (3 + sin x) 2 × x; з) у = ;
б) у = 3х × sin 5x + 8; ж) у =х× (cos ln x + sin lnx);
в) у = (3 + sin x) 2 × x; з) у =  ;
г) у = ;
г) у =  ; и) у = 0,92 ; и) у = 0,92  ;
д) у = ;
д) у = 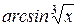 ; к) у = ; к) у =  . .
|






