ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ХАМЗИНА БОЛАШ САПИДОЛЛИЕВНА
ЭКЗАМЕНАЦИОННЫЕ ТЕСТОВЫЕ ЗАДАНИЯ – 200 ВОПРОСОВ
ТЕСТЫ ОТ 12 НОЯБРЯ 2012 ГОДА.
TESTS-1-RUS-VT-VT3-TEOR.VER.-HAMZINA-AVT.test
1. Событие, исход которого является единственно возможным в данном испытании, называется = ДОСТОВЕРНЫМ
2. К доске наугад вызывают одного ученика. Событие 
- получение оценки «хорошо», событие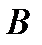 
- получение оценки «удовлетворительно». Что означает событие 
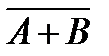= УЧЕНИК УЧИТСЯ НА «НЕУДОВЛЕТВОРИТЕЛЬНО»
3. Из колоды из 36 карт наугад берется одна. Вероятность того, что вынута карта будет с рисунком (король, дама, валет), равна = 1/3
4. Набирая номер телефона, абонент забыл последнюю цифру и набрал ее наудачу. Вероятность того, что номер набран правильно, равна = 1/10
5. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Вероятность того, что номер наудачу извлеченного жетона не содержит цифры 5, равна = 0,81
6. В лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Вероятность какого-либо выигрыша равна = 0,2
7. Брошены две монеты. Вероятность появления герба на обеих монетах равна = 1/4
8. Вероятность случайного события равна = ЛЮБОЕ ЧИСЛО МЕЖДУ 0 И 1
9. Может ли событие наступить с отрицательной вероятностью = НЕТ
10. Студент знает 20 из 25 программы. Найти вероятность того, что студент знает предложенные ему экзаменатором два вопроса = 19/30
11. Сколько всевозможных исходов при одном бросании игральной кости = 6
12. Вероятность появления нечетного очка при бросании монеты равна = 1/2
13. Бросают две игральной кости. Вероятность того, что сумма выпавших очков будет кратной 6-ти, равна = 1/6
14. При стрельбе была получена частость попадания 0,9. Найти число попаданий в цель, если сделано 140 выстрелов = 126
15. Отдел технического контроля при проверке 200 изделий обнаружил 8 нестандартных. Найти относительную частоту появления нестандартного изделия = 0,04
16. Сколько всевозможных исходов при одном бросании трех игральных костей = 216
17. Из 24 выстрелов было получено19 попаданий. Найти частость попадания = 19/24
18. В ящике 50 деталей, из них 5 окрашенных. Вероятность того, что взятая наудачу деталь окажется окрашенной, равна = 0,01
19. При стрельбе была получена частость попадания 0,85. Сколько было попаданий, если сделано 120 выстрелов = 102
20. В ящике 10 красных, 5 синих, 15 белых шаров. Вероятность того, что наудачу взятый шар окажется окрашенным, равна = 0,5
21. Из натуральных чисел от 1 до 20 наугад берется одно число. Вероятность того, что взятое число делится на 4, равна = 0,25
22. В урне шары с номерами от 1 до 5. Один за другим наугад извлекаются 3 шара. Вероятность того, что взятые шары с четными номерами, равна = 0
23. Из натуральных чисел от 1 до 20 наугад берется одно число. Вероятность того, что взятое число является делителем числа 20, равна = 0,3
24. Из множества двузначных чисел наугад берется одно число. Вероятность того, что взятое число состоит из одинаковых цифр, равна = 0,1
25. Вероятность того, что квадрат наугад взятого однозначного числа заканчивается цифрой 9, равна = 0,2
26. Может ли событие наступить с вероятностью -1/2 = НЕТ
27. Из натуральных чисел от 1 до 30 наугад берется одно число. Вероятность того, что взятое число является кратным числу 10, равна = 0,3
28. Бросают две игральные кости. Вероятность того, что произведение выпавших очков будет равно 15, равна = 1/18
29. В классе 15 девочек и 12 мальчиков. Вероятность того, наугад вызванный к доске ученик окажется мальчиком, равна = 4/9
30. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Вероятность того, что номер наудачу извлеченного жетона содержит цифру 0, равна = 0,1
31. В урне 8 красных, 3 синих, 9 белых шаров. Вероятность того, что наудачу взятый шар окажется синим, равна = 0,15
32. В урне 8 красных, 3 синих, 9 белых шаров. Вероятность того, что наудачу взятый шар окажется красным, равна = 0,4
33. Формула вероятности суммы совместимых событий =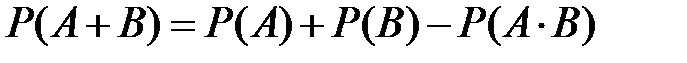 
34. Формула вероятности произведения зависимых событий =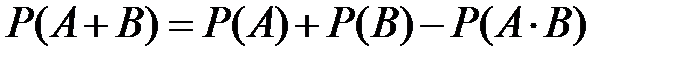 
35. Вероятность выпадения 7 очков при бросании двух игральных костей равна = 0
36. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =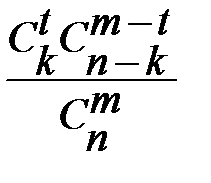 
37. Сколько знаков можно составить из 6 разноцветных флажков, если берется по два флажка
= 
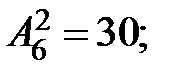
38. Найти формулу числа сочетаний =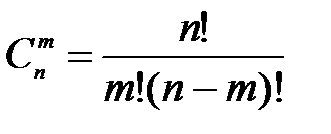 
39. Найти формулу числа размещений =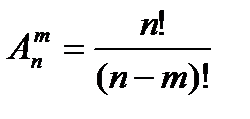 
40. Ребенок играет с четырьмя буквами из разрезной азбуки Д, Л, А, А. Вероятность того, что при случайном расположении букв в ряд он получит слово «ДАЛА», равна = 1/12
41. Вероятность того, что при случайном расположении букв А, В, К, М, О, С в ряд получится слово «МОСКВА», равна = 1/720
42. Найти формулу числа перестановок = Рn= n(n-1)(n-2)…3•2•1=n!
43. Ребенок играет с четырьмя буквами из разрезной азбуки М, Л, А, А. Вероятность того, что при случайном расположении букв в ряд он получит слово «АЛМА», равна = 1/12
44. Сколькими способами можно переставить книги из 30 томов так, чтобы 1 и 2 тома находились рядом = 29!
45. Вероятность того, что наугад взатая буква из слова «АЛМАТЫ» окажется гласной, равна
= 1/3
46. Ребенок играет с четырьмя буквами из разрезной азбуки Ш, Л, А, А. Вероятность того, что при случайном расположении букв в ряд он получит слово «АЛША», равна = 1/12
47. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются = 
48. Сколькими способами можно выбрать две детали из 10 деталей =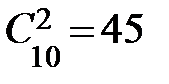 
49. В урне 15деталей, из них 10 окрашенных. Вероятность того, что взятые наудачу три детали окажутся окрашенными, равна =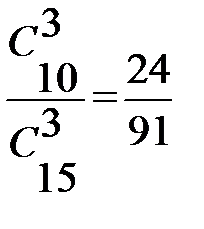 
50. В коробке 5 изделий, из них 3 окрашенных. Вероятность того, что среди взятых наудачу двух изделий хотя бы одно окажется окрашенным, равна = 0,9
51. Карточки с буквами А, Д, К, С, Н наугад распологаются в ряд. Вероятность того, что получится слово «САН», равна = 1/60
52. Карточки с буквами А, А, М, М наугад распологаются в ряд. Вероятность того, что получится слово «МАМА», равна = 1/6
53. Для каких событий верно равенство P(A·B)=P(A)·P(B) = А, В- НЕЗАВИСИМЫЕ СОБЫТИЯ
54. Для каких событий верно равенство P(AB)=P(A)·PА(B) = А, В- НЕЗАВИСИМЫЕ СОБЫТИЯ
55. Что означает символ PА(В) = ВЕРОЯТНОСТЬ СОБЫТИЯ В, ВЫЧИСЛЕННАЯ В ПРЕДПОЛОЖЕНИИ, ЧТО СОБЫТИЕ А НАСТУПИЛО
56. Что означает символ PB(A) = ВЕРОЯТНОСТЬ СОБЫТИЯ А, ВЫЧИСЛЕННАЯ В ПРЕДПОЛОЖЕНИИ, ЧТО СОБЫТИЕ В НАСТУПИЛО
57. Что означает символ PАВ(С) = ВЕРОЯТНОСТЬ СОБЫТИЯ С, ВЫЧИСЛЕННАЯ В ПРЕДПОЛОЖЕНИИ, ЧТО СОБЫТИЯ А И В НАСТУПИЛИ
58. Из колоды в 36 карт наугад извлекают 2 карты. Вероятность вынуть король при втором испытании, если первым также вынут король, равна = 3/35
59. Из партии 40 стандартных и 4 не стандартных деталей на проверку наугад взяли 8 деталей. Они оказались стандартными. Вероятность того, что взятая наугад следующая деталь окажется стандартной, равна = 8/9
60. Из колоды в 36 карт наугад извлекают 2 карты. Вероятность вынуть туз при втором испытании, если первым также вынут туз, равна = 3/35
61. В урне 10 деталей, из них 6 окрашенных. Из урны наугад вынимают 4 детали. Вероятность того, что все детали окажутся окрашенными, равна = 1/14
62. В ящике находятся шары с номерами от 1 до 5. Наугад извлекают 4 шара. Вероятность того, что все шары окажутся с нечетными номерами, равна = 0
63. В ящике находятся шары с номерами от 1 до 5. Наугад извлекают 4 шара. Вероятность того, что все шары окажутся с четными номерами, равна = 0
64. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Вероятность появления белого шара при втором испытании, если первым извлечен черный шар, равна = 0,3
65. Из колоды в 36 карт наугад извлекают 2 карты. Вероятность вынуть валет при втором испытании, если при первом испытании вынут туз, равна = 4/35
66. В каждой из двух урн содержится 10 деталей. В первой урне 8, во второй урне 7 стандартных деталей. Из каждой урны наугад извлекают по одной детали. Вероятность того, что обе извлеченные детали окажутся стандартными, равна = 0,56
67. В урне 5 белых и 4 черных шаров. Из урны трижды вынимают по одному шару, не возвращая их обратно. Вероятность того, что все извлеченные шары окажутся белыми, равна = 0,12
68. Студент пришел на экзамен, зная из 25 вопросов только 20. Преподаватель задает два вопроса. Вероятность того, что студент ответит на оба вопроса, равна = 19/30
69. В урне 10 деталей, из них 6 окрашенных. Из урны наугад вынимают 4 детали. Вероятность того, что все детали окажутся неокрашенными, равна = 1/210
70. Три стрелка независимо друг от друга по одному разу стреляли по мишени соответственно с вероятностью попадания: 0,6; 0,7; 0,8. Вероятность не попадания в мишень всех стрелков равна = 0,024
71. Формула вероятности суммы совместимых событий =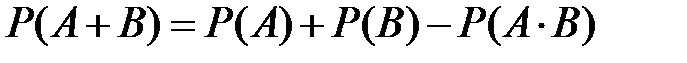
72. Формула вероятности произведения зависимых событий =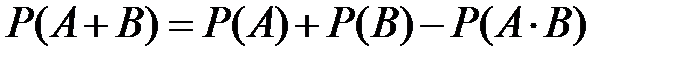
73. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =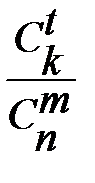 
74. Сколько знаков можно составить из 6 разноцветных флажков, если берется по два флажка
= 
75. Найти формулу числа сочетаний =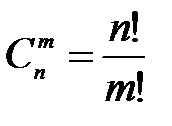 
76. Найти формулу числа размещений =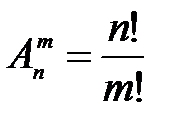 
77. Найти формулу числа размещений =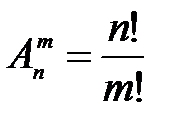
78. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
79. Сколькими способами можно выбрать две детали из 10 деталей =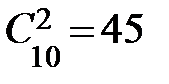
80. Сколько всевозможных исходов при одном бросании игральной кости = 6
81. При стрельбе была получена частость попадания 0,9. Найти число попаданий в цель, если сделано 140 выстрелов = 126
82. Сколько всевозможных исходов при одном бросании трех игральных костей = 216
83. При стрельбе была получена частость попадания 0,85. Сколько было попаданий, если сделано 120 выстрелов = 102
84. Формула вероятности суммы совместимых событий =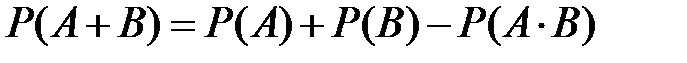
85. Формула вероятности произведения зависимых событий =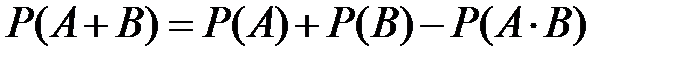
86. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =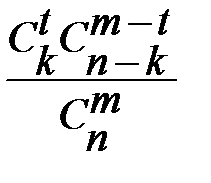
87. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
88. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
89. Сколькими способами можно выбрать две детали из 10 деталей =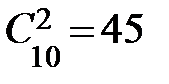
90. В урне 15деталей, из них 10 окрашенных. Вероятность того, что взятые наудачу три детали окажутся окрашенными, равна =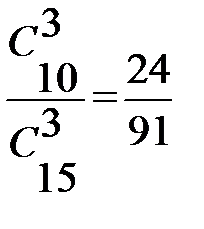
91. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Вероятность появления белого шара при втором испытании, если первым извлечен черный шар, равна = 0.3
92. В каждой из двух урн содержится 10 деталей. В первой урне 8, во второй урне 7 стандартных деталей. Из каждой урны наугад извлекают по одной детали. Вероятность того, что обе извлеченные детали окажутся стандартными, равна = 0.56
93. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
94. Сколькими способами можно выбрать две детали из 10 деталей =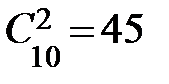
95. В урне 15деталей, из них 10 окрашенных. Вероятность того, что взятые наудачу три детали окажутся окрашенными, равна =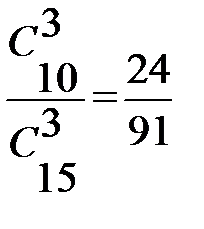
96. В коробке 5 изделий, из них 3 окрашенных. Вероятность того, что среди взятых наудачу двух изделий хотя бы одно окажется окрашенным, равна = 0.9
97. Из партии 40 стандартных и 4 не стандартных деталей на проверку наугад взяли 8 деталей. Они оказались стандартными. Вероятность того, что взятая наугад следующая деталь окажется стандартной, равна = 8/9
98. Из колоды в 36 карт наугад извлекают 2 карты. Вероятность вынуть король при втором испытании, если первым также вынут король, равна = 3/35
99. В ящике находятся шары с номерами от 1 до 5. Наугад извлекают 4 шара. Вероятность того, что все шары окажутся с нечетными номерами, равна = 0
100. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Вероятность появления белого шара при втором испытании, если первым извлечен черный шар, равна = 0.3
101. Студент пришел на экзамен, зная из 25 вопросов только 20. Преподаватель задает два вопроса. Вероятность того, что студент ответит на оба вопроса, равна = 19/30
102. Формула вероятности суммы совместимых событий =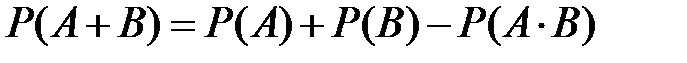
103. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =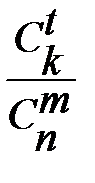
104. Сколько знаков можно составить из 6 разноцветных флажков, если берется по два флажка
=
105. Найти формулу числа сочетаний =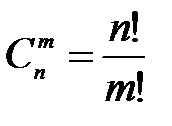
106. Найти формулу числа размещений =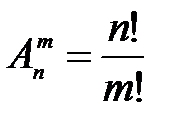
107. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
108. Формула вероятности произведения зависимых событий
=
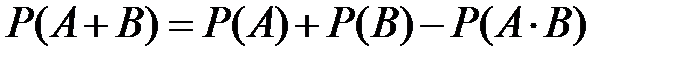
109. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
110. Сколькими способами можно выбрать две детали из 10 деталей =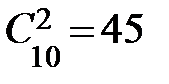
111. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
112. Три стрелка независимо друг от друга по одному разу стреляли по мишени соответственно с вероятностью попадания: 0,6; 0,7; 0,8. Вероятность не попадания в мишень всех стрелков равна = 0.024
113. Формула вероятности произведения зависимых событий
=
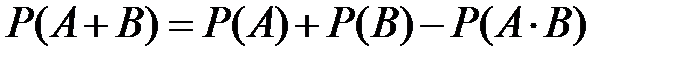
114. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =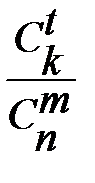
115. Сколько всевозможных исходов при одном бросании трех игральных костей = 216
116. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
117. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =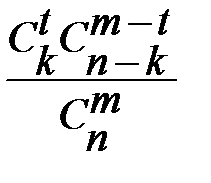
118. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
119. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
120. Сколькими способами можно выбрать две детали из 10 деталей =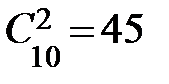
121. Сколько всевозможных исходов при одном бросании игральной кости = 6
122. При стрельбе была получена частость попадания 0,9. Найти число попаданий в цель, если сделано 140 выстрелов = 126
123. В каждой из двух урн содержится 10 деталей. В первой урне 8, во второй урне 7 стандартных деталей. Из каждой урны наугад извлекают по одной детали. Вероятность того, что обе извлеченные детали окажутся стандартными, равна = 0.56
124. Формула вероятности суммы совместимых событий =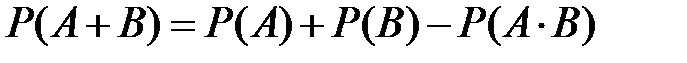
125. Сколькими способами можно выбрать две детали из 10 деталей =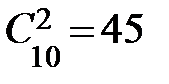
126. В урне 15деталей, из них 10 окрашенных. Вероятность того, что взятые наудачу три детали окажутся окрашенными, равна =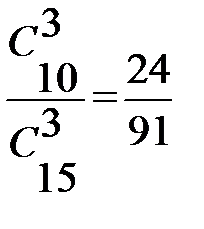
127. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
128. Из партии 40 стандартных и 4 не стандартных деталей на проверку наугад взяли 8 деталей. Они оказались стандартными. Вероятность того, что взятая наугад следующая деталь окажется стандартной, равна = 8/9
129. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
130. Найти формулу числа размещений =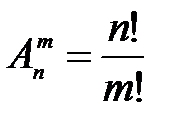
131. Сколькими способами можно выбрать две детали из 10 деталей =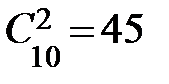
132. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
133. Три стрелка независимо друг от друга по одному разу стреляли по мишени соответственно с вероятностью попадания: 0,6; 0,7; 0,8. Вероятность не попадания в мишень всех стрелков равна = 0.024
134. Сколькими способами можно выбрать две детали из 10 деталей =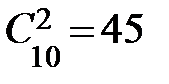
135. Формула вероятности суммы совместимых событий =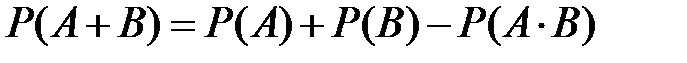
136. Сколькими способами можно выбрать две детали из 10 деталей =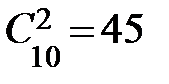
137. Набирая номер телефона, абонент забыл последнюю цифру и набрал ее наудачу. Вероятность того, что номер набран правильно, равна = 1/10
138. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Вероятность того, что номер наудачу извлеченного жетона не содержит цифры 5, равна = 0.81
139. Брошены две монеты. Вероятность появления герба на обеих монетах равна = 1.4
140. При стрельбе была получена частость попадания 0,9. Найти число попаданий в цель, если сделано 140 выстрелов = 126
141. Отдел технического контроля при проверке 200 изделий обнаружил 8 нестандартных. Найти относительную частоту появления нестандартного изделия = 0.04
142. При стрельбе была получена частость попадания 0,85. Сколько было попаданий, если сделано 120 выстрелов = 102
143. В урне шары с номерами от 1 до 5. Один за другим наугад извлекаются 3 шара. Вероятность того, что взятые шары с четными номерами, равна = 0
144. Формула вероятности суммы совместимых событий =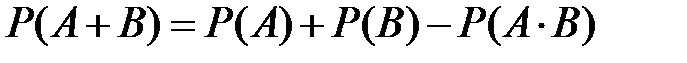
145. Вероятность того, что наугад взатая буква из слова «АЛМАТЫ» окажется гласной, равна = 1/3
146. Сколько всевозможных исходов при одном бросании трех игральных костей = 216
147. В каждой из двух урн содержится 10 деталей. В первой урне 8, во второй урне 7 стандартных деталей. Из каждой урны наугад извлекают по одной детали. Вероятность того, что обе извлеченные детали окажутся стандартными, равна = 0.56
148. Из колоды в 36 карт наугад извлекают 2 карты. Вероятность вынуть король при втором испытании, если первым также вынут король, равна = 3/35
149. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
150. Из множества двузначных чисел наугад берется одно число. Вероятность того, что взятое число состоит из одинаковых цифр, равна = 0.1
151. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Вероятность появления белого шара при втором испытании, если первым извлечен черный шар, равна = 0.3
152. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
153. Три стрелка независимо друг от друга по одному разу стреляли по мишени соответственно с вероятностью попадания: 0,6; 0,7; 0,8. Вероятность не попадания в мишень всех стрелков равна = 0.024
154. В урне шары с номерами от 1 до 5. Один за другим наугад извлекаются 3 шара. Вероятность того, что взятые шары с четными номерами, равна = 0
155. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
156. Событие, исход которого является единственно возможным в данном испытании, называется = достоверным
157. Набирая номер телефона, абонент забыл последнюю цифру и набрал ее наудачу. Вероятность того, что номер набран правильно, равна = 1/10
158. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
159. Найти формулу числа сочетаний =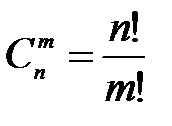
160. Найти формулу числа размещений =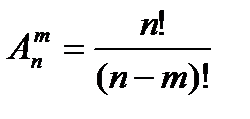
161. Три стрелка независимо друг от друга по одному разу стреляли по мишени соответственно с вероятностью попадания: 0,6; 0,7; 0,8. Вероятность не попадания в мишень всех стрелков равна = 0.024
162. При стрельбе была получена частость попадания 0,9. Найти число попаданий в цель, если сделано 140 выстрелов = 126
163. Вероятность появления нечетного очка при бросании монеты равна = 1/2
164. В ящике находятся шары с номерами от 1 до 5. Наугад извлекают 4 шара. Вероятность того, что все шары окажутся с четными номерами, равна = 0
165. Формула вероятности суммы совместимых событий =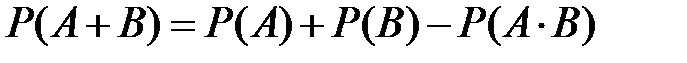
166. Формула вероятности произведения зависимых событий =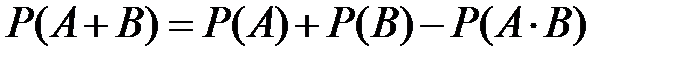
167. Найти формулу числа размещений =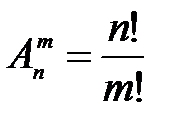
168. Из партии 40 стандартных и 4 не стандартных деталей на проверку наугад взяли 8 деталей. Они оказались стандартными. Вероятность того, что взятая наугад следующая деталь окажется стандартной, равна = 8/9
169. Сколько всевозможных исходов при одном бросании трех игральных костей = 216
170. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Вероятность того, что номер наудачу извлеченного жетона не содержит цифры 5, равна = 0,81
171. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
172. В партии из n изделий k бракованных. Вероятность того, что среди наудачу взятых для проверки m изделий ровно t окажутся бракованными, равна =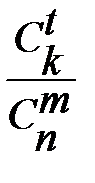
173. Сколькими способами можно выбрать две детали из 10 деталей =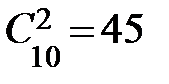
174. Событие, исход которого является единственно возможным в данном испытании, называется = достоверным
175. Студент знает 20 из 25 программы. Найти вероятность того, что студент знает предложенные ему экзаменатором два вопроса = 19/30
176. Отдел технического контроля при проверке 200 изделий обнаружил 8 нестандартных. Найти относительную частоту появления нестандартного изделия = 0,04
177. Карточки с буквами А, Д, К, С, Н наугад распологаются в ряд. Вероятность того, что получится слово «САН», равна = 1/60
178. Сколько всевозможных исходов при одном бросании игральной кости = 6
179. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
180. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
181. Сколькими способами можно выбрать две детали из 10 деталей =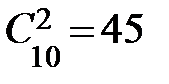
182. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Вероятность появления белого шара при втором испытании, если первым извлечен черный шар, равна = 0.3
183. При стрельбе была получена частость попадания 0,85. Сколько было попаданий, если сделано 120 выстрелов = 102
184. В урне шары с номерами от 1 до 5. Один за другим наугад извлекаются 3 шара. Вероятность того, что взятые шары с четными номерами, равна = 0
185. Формула вероятности суммы совместимых событий =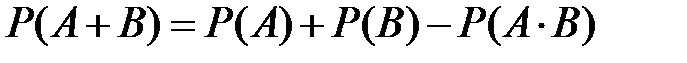
186. Сколькими способами можно выбрать две детали из 10 деталей =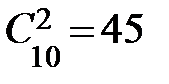
187. Сколькими способами можно выбрать две детали из 10 деталей =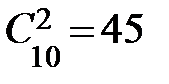
188. В каждой из двух урн содержится 10 деталей. В первой урне 8, во второй урне 7 стандартных деталей. Из каждой урны наугад извлекают по одной детали. Вероятность того, что обе извлеченные детали окажутся стандартными, равна =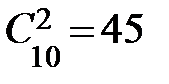
189. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
190. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
191. Найти формулу числа размещений =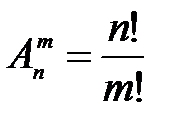
192. Из колоды в 36 карт наугад извлекают 2 карты. Вероятность вынуть король при втором испытании, если первым также вынут король, равна = 3/35
193. Найти формулу числа размещений =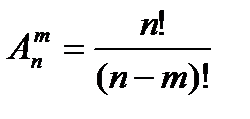
194. Сколькими способами можно выбрать две детали из 10 деталей =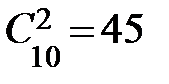
195. Формула вероятности суммы совместимых событий =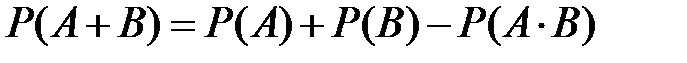
196. Найти формулу числа размещений =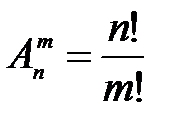
197. В каждой из двух урн содержится 10 деталей. В первой урне 8, во второй урне 7 стандартных деталей. Из каждой урны наугад извлекают по одной детали. Вероятность того, что обе извлеченные детали окажутся стандартными, равна = 0.56
198. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
199. В лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Вероятность какого-либо выигрыша равна = 0.2
200. Сколько трехзначных чисел можно получить с помощью цифр1,2,3, если цифры в одном числе не повторяются =
