Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1

Нормальное распределение при и называется стандартным нормальным распределением.

Плотность стандартного нормального распределения имеет вид при любом , а функция распределения

табулирована (то есть ее значения вычислены при многих ) почти во всех математических справочниках.

 

25. Вероятность попадания нормальной случайной величины в заданный интервал. Правила сигм. Известно, что если случайная величина X задана плотностью распределения , то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:

.

Пусть случайная величина X распределена по нормальному закону. Тогда

.

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную . Отсюда .

Найдем новые пределы интегрирования. Если , то , если , то . Тогда

.

Выражение , входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем:

Ф — Ф ,

где Ф(x) = .

Эту формулу называют формулой Лапласа.

Если случайная величина X является признаком генеральной совокупности, то формула Лапласа дает долю элементов генеральной совокупности, у которых значение признака X находится в границах от до .

Интеграл, через который выражается функция Лапласа, нельзя выразить через элементарные функции. Его можно представить в виде степенного ряда, если разложить в ряд подынтегральную функцию и почленно проинтегрировать ряд. Тогда

Ф(x) = .

C помощью этого ряда можно вычислить значение Ф(x) для любого x с любой точностью. Составлены специальные таблицы значений функции Лапласа.

Отметим ряд свойств функции Лапласа, полезных для применения.

1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).

2. Функция Ф(x) – возрастающая, быстро приближающаяся к своему пределу, равному 0,5: Ф(0) = 0, Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986, Ф(4) = 0,4999 и т.д. На практике полагают Ф(x) для x>5.

Правила двух и трех сигм

Если в формуле (1) принять последовательно d = 2s и d = 3s, то получим: (2) (3) Правило двух сигм. Почти достоверно (с доверительной вероятностью 0,954) можно утверждать, что все значения случайной величины X с нормальным законом распределения отклоняются от ее математического ожидания M(X) = a на величину, не большую 2s (двух средних квадратических отклонений). Доверительной вероятностью Pд называют вероятность событий, которые условно принимаются за достоверные (их вероятность близка к 1). При решении вопросов, требующих большей надежности, когда доверительную вероятность принимают равной 0,997, вместо правила двух сигм, согласно формуле (3), используют правило трех сигм. Проиллюстрируем правило двух сигм геометрически. На рис. 6 изображена кривая Гаусса с центром распределения а. Площадь, ограниченная всей кривой и осью Оx, равна 1 (100%), а площадь криволинейной трапеции между абсциссами а–2s и а+2s, согласно правилу двух сигм, равна 0,954 (95,4% от всей площади). Площадь заштрихованных участков равна 1-0,954 = 0,046 (»5% от всей площади). Эти участки называют критической областью значений случайной величины. Значения случайной величины, попадающие в критическую область, маловероятны и на практике условно принимаются за невозможные. Вероятность условно невозможных значений называют уровнем значимости случайной величины. Уровень значимости связан с доверительной вероятностью формулой = 1- , где q – уровень значимости, выраженный в процентах. Согласно правилу трех сигм при доверительной вероятности 0,997 критической областью будет область значений признака вне интервала (а-3s, а+3s). Уровень значимости составляет 0,3%. Уровень значимости принимают различным в зависимости от дозволенной степени риска. В текстильной и швейной промышленности его принимают равным 5%. С помощью правила двух (или трех) сигм можно определить общий интервал изменения той или иной случайной величины с нормальным законом распределения.

 

26. Неравенство Чебышева и его применение. Закон больших чисел играет важную роль в практическом применении теории вероятности.

Свойство случайных величин вести себя (при определенных условиях) практически как не случайные позволяет уверенно оперировать с этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.

 

Неравенство Чебышева оценивает вероятность того, что отклонение случайных величин х от М[x] не превзойдет заданное положительное число e.. Для любой случайной величины справедлива

заданное положительное число ("e> 0)

Эта вероятность тем меньше, чем меньше дисперсия, в качестве характеристики рассеяния. Приведем доказательство для непрерывных случайных величин, известно, что

f(x) – плотность распределения.

Интеграл в правой части распространяется как интервалы от -∞ до а –e и от а – e до ∞. В этих интервалах имеет место следующее неравенство. Возьмем данный интервал и возведем в квадрат , так как f(x) – неотрицательная функция f(x) > 0 умножим обе части на f(x) и проинтегрируем.

,

В силу положительности подинтегральной функции можно перейти к интегралу: -∞; +∞

(1)

другая формула неравенства (1). Если (х-а) < e, то

(2)

 

27. Математическая статистика, её задачи.

Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений.

Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений.

Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть:

- оценка неизвестной вероятности события;

- оценка параметров распределения случайной величины;

- оценка неизвестной функции распределения случайной величины;

- проверка гипотез о параметрах распределения или о виде неизвестного распределения;

- оценка зависимости случайной величины от одной или нескольких случайных величин и т.д.

Случайную величину будем называть генеральной совокупностью .

Исходным материалом для изучения свойств генеральной совокупности являются статистические данные, т.е. значения , полученные в результате повторения случайного опыта (измерения случайной величины ). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины , , заданной на множестве исходов -го опыта, не зависит от и совпадает с распределением генеральной совокупности .

Набор независимых в совокупности случайных величин , где соответствует -му опыту, называют случайной выборкой из генеральной совокупности . Число называется объёмом выборки.

Совокупность чисел , полученных в результате -кратного повторения опыта по измерению генеральной совокупности , называется реализацией случайной выборкиили просто выборкой объёма .

В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности устанавливаются путём изучения тех же свойств на случайной выборке.

 

28. Вариационные ряды и их графическое изображение

Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, её объём.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %.

В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды. Удобно ряды распределения анализировать при помощи графического изображения, позволяющего судить и о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма. Полигон используется при изображении дискретных вариационных рядов. На оси ординат могут наноситься не только значения частот, но и частостей вариационного ряда.
Гистограмма принимается для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам. Гистограмма – график, на котором ряд изображен в виде смежных друг с другом столбиков. Изображение вариационного ряда в виде кумуляты особенно эффективно для вариационных рядов, частоты которых выражены в долях или процентах к сумме частот ряда.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять, то мы получим огиву. Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями. При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах.
Плотность распределения – это частота, рассчитанная на единицу ширины интервала, т.е. сколько единиц в каждой группе приходится на единицу величины интервала. Для графического изображения вариационных рядов может также использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путём последовательно суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты.

 

29. Основные характеристики вариационного ряда

Наиболее распространенной мерой уровня – является средняя арифметическая.

где - знак суммирования от 1 до k; X_i – варианты с порядковым номером i; = n – объем совокупности (число элементов совокупности); n_i – частота варианта x_i; k – число варианта. Если вместо частоты заданы частости q_i, то формула имеет вид

где = 1, или 100%. Медианой (обозначим M_е) называется такое значение варьирующего признака, которое приходится на середину вариационного ряда.
При нахождении медианы дискретного вариационного ряда могут возникнуть два случая: 1) число вариант нечетно (k=2m+1), 2) число вариант четно (k=2m). В первом случае M_e=x_m+1, т. е. медиана равна центральной (срединной) варианте ряда, во втором случае M_e,=(x_m+x_m+1)/2, т.е. медиана принимается равной полу сумме находящихся в середине ряда вариант. Для интервального вариационного ряда медиана вычисляется по формуле

где x_Me(min)-нижняя граница медианного интервала; h - величина этого интервала, или интервальная разность; q_i- частоты или частости; 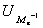- накопленная сверху частота (или частость) интервала, предшествующего медианному; частота или частость медианного интервала. Модой (обозначим М_о) называется варианта, наиболее часто встречающаяся в данном вариационном ряду.
Для дискретного ряда мода равна варианте с наибольшей частотой или частостью.
Для интервального вариационного ряда модальный интервал, т. е. интервал, содержащий моду, определяется по наибольшей' частоте (частости) в случае равных интервалов и по наибольшей плотности в случае неравных интервалов. Значение варианты, равное моде, отыскивается приближенными методами.
Довольно грубое приближение можно получить, взяв за моду центральное значение модального интервала, т. е. среднее арифметическое границ интервала. Размах вариации показывает разность между наибольшим и наименьшим значениями признака (R=x_max-x_min). Достоинством этого показателя является простота расчета. Однако возможности его применения ограничены, так как эта характеристика является наиболее грубой из всех мер рассеяния. Дисперсия, или средний квадрат отклонения (обозначим σ²) есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической, т. е. в математической записи

где x_i-варианта с порядковым номером i; - средняя арифметическая; k- число вариант; q_i-частота или частость с порядковым номером I.
Часто для исследования удобно представлять меру рассеяния в тех же единицах измерения, что и варианты. Тогда вместо дисперсии используют среднее квадратичное отклонение, которое является квадратным корнем из дисперсии, т. е. среднее квадратичное отклонение вычисляется по формуле
Коэффициент вариации (обозначим V) представляет собой отношение среднего квадратичного отклонения к средней арифметической, выраженное в процентах, т. е.

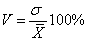
Коэффициент вариации позволяет: 1) сравнивать вариацию одного и того же признака у разных групп объектов, 2) выявить степень различия одного и того же признака у одной и той же группы объектов в разное время, 3) сопоставить вариацию разных признаков у одних и тех же групп объектов.

 

30. Доверительные интервалы и доверительная вероятность. Наряду с точечными широко применяют интервальные оценки числовых характеристик случайных величин, выражающеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерения. Вероятность того, что погрешность не выйдет за границы некоторого интервала, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс (квантилями), что показано на рис. 1.10.

Рис.1.10.

Таким образом, интервал , за границы которого погрешность не выйдет с некоторой вероятностью, называется доверительным интервалом, а характеризующая его вероятность - доверительной вероятностью. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интервалом и по нему определять доверительную вероятность, либо, наоборот, по доверительной вероятности подсчитывать доверительный интервал. Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95 и даже 0,90.

Доверительный интервал обычно выражают через относительную величину в долях среднего квадратического отклонения (“кратность”) . Для нормального закона доверительную вероятность определяют по значениям интеграла вероятности (функции Лапласа), который в математической справочной литературе обозначается и определяется

Зная доверительные границы и можно определить доверительную вероятность

Если значения доверительных границ и симметричны, т.е.

, то и .

Тогда

Для наиболее часто встречающихся значений доверительной вероятности в табл. 1.3 указаны соответствующие значения кратности.

Таблица 1.3

P(t)	0,90	0,95	0,99	0,999
t	1,645	1,960	2,576	3,291

При нормальном законе распределения доверительный интервал имеет доверительную вероятность =0,9973, что означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше . На основании этого основан один из критериев грубых погрешностей, когда остаточная погрешность какого-либо результата измерения превышает значение , то этот результат считается промахом и исключается из ряда измерений.

 

31. Проверка статистических гипотез. Ошибки первого, второго рода

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки [3, 5, 11]. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называютнепараметрическими, в противном случае – параметрическими.

Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н₀. Наряду с основной гипотезой рассматривают иальтернативную (конкурирующую, противоречащую) ей гипотезу Н₁. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.

Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если является параметром экспоненциального распределения, то гипотеза Н₀ о равенстве  =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н₀ о неравенстве  >10 состоит из бесконечного множества простых гипотез Н₀ о равенстве =b_i , где b_i – любое число, большее 10. Гипотеза Н₀ о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x₁, x₂, …, x_n). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S₀ и S₁. Если значение критерия z попадает в область S₀, то гипотеза принимается, а если в область S₁, – гипотеза отклоняется. Множество S₀ называется областью принятия гипотезы или областью допустимых значений, а множество S₁ – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.

Принятие или отклонение гипотезы Н₀ по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью  тогда, когда отвергается верная гипотеза Н₀ и принимается конкурирующая гипотеза Н₁. Ошибка второго рода возникает с вероятностью  в том случае, когда принимается неверная гипотеза Н₀, в то время как справедлива конкурирующая гипотеза Н₁. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н₀. Вероятность отвергнуть ложную гипотезу Н₀ называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл. 3.1.

Таблица 3.1.

Гипотеза Н0	Решение	Вероятность	Примечание
Верна	Принимается	1–	Доверительная вероятность
Отвергается		Вероятность ошибки первого рода
Неверна	Принимается		Вероятность ошибки второго рода
Отвергается	1–	Мощность критерия

Например, рассмотрим случай, когда некоторая несмещенная оценка параметра  вычислена по выборке объема n, и эта оценка имеет плотность распределения f(), рис. 3.1.

Рис. 3.1. Области и отклонения гипотезы

Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н₀ о равенстве  =Т, то насколько велико должно быть различие между  и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между  и Т на основе выборочного распределения параметра .

Целесообразно полагать одинаковыми значения вероятности выхода параметра  за нижний и верхний пределы интервала. Такое допущение во многих случаях позволяет минимизировать доверительный интервал, т.е. повысить мощность критерия проверки. Суммарная вероятность того, что параметр  выйдет за пределы интервала с границами  _{1– /2} и   _/2, составляет величину . Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства =Т можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания отвергнуть гипотезу Н₀. Отсюда следует, что вероятность допустить ошибку первого рода равна  (равна уровню значимости критерия).

Если предположить, например, что истинное значение параметра в действительности равно Т+d, то согласно гипотезе Н₀ о равенстве  =Т – вероятность того, что оценка параметра  попадет в область принятия гипотезы, составит , рис. 3.2.

При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости . Однако при этом увеличивается вероятность ошибки второго рода  (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т– d.

Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность  была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения  относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами  _{1– /2} и   _/2 для типовых значений  и различных способов построения критерия.

При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия.

В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента.

 

32.Обработка результатов измерений. Оценка генерального среднего.

 

1.1.Генеральная средняя.

Пусть изучается генеральная совокупность относительно количественного признака Х.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если все значения признака различны, то

Если значения признака имеют частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

 

34.проверка гипотезы о равестве дисперсий двух генеральных совокупностей Пусть из двух нормально распределенных генеральных совокупностей извлечены выборки объема и соответственно. По этим выборкам вычислены несмещенные оценки дисперсий и . Для проверки нулевой гипотезы о равенстве дисперсий генеральных совокупностей против одной из альтернативных ( – двусторонняя критическая область, или – односторонняя критическая область) используется случайная величина

,

здесь в числителе дроби стоит максимальная оценка дисперсии из и , в знаменателе – минимальная. Если нулевая гипотеза верна, то статистика распределена по закону Фишера-Снедекора как отношение двух случайных величин, имеющих распределение и ( – число степеней свободы числителя; – число степеней свободы знаменателя).

Действительно, если , для определенности будем полагать , то

где , .

По таблице распределения Фишера-Снедекора (прил. 5) для заданного уровня значимости определяется критическое значение статистики для двусторонней критической области и 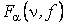– для односторонней критической области.

Вычисленное значение статистики сравнивается с критическим. Если , то при уровне значимости нулевую гипотезу считают непротиворечащей опытным данным. Если же , то нулевая гипотеза отвергается в пользу конкурирующей.

 

 

35. Проверка гипотезы о равенстве средних значений двух совокупностей

Сформулируем задачу. Пусть имеются две совокупности, характеризуемые генеральными средними и 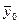и известными дисперсиями и . Необходимо проверить гипотезу о равенстве генеральных средних, т.е. : = 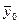. Для проверки гипотезы из этих совокупностей взяты две независимые выборки объемов и , по которым найдены средние арифметические и и выборочные дисперсии и .При достаточном больших объемов выборки, выборочные средние и имеют приближенно нормальный закон распределения, соответственно и .В случае справедливости гипотезы разность - имеет нормальный закон распределения с математическим ожиданием и дисперсией .

Поэтому при выполнении гипотезы статистика

 

 

имеет стандартное нормальное распределение N (0; 1).

 

36.Исключение грубых ошибок при обработке данных эксперимента
При получении результата измерения, резко отличающегося от всех других результатов, возникает подозрение, что допущена грубая ошибка. В этом случае необходимо сразу же проверить, не нарушены ли основные условия измерения. Если же такая проверка не была сделана вовремя, то вопрос о целесообразности браковки резко отличающихся значений решается путем сравнения его с остальными результатами измерений. При этом применяются различные критерии, в зависимости от того, известна или нет средняя квадратическая ошибка s_i измерений (предполагается, что все измерения производятся с одной и той же точностью и независимо друг от друга).
Метод исключения при известной s_i. Сначала определяется коэффициент t по формуле
, (5.1)
где x* – резко выделяющееся значение (предполагаемая ошибка). Значение определяется по формуле (2.1) без учета предполагаемой ошибки x*.
Далее задаются уровнем значимости a, при котором исключаются ошибки, вероятность появления которых меньше величины a. Обычно используют один из трех уровней значимости: 5 % уровень (исключаются ошибки, вероятность появления которых меньше 0.05); 1 % уровень (соответственно меньше 0.01) и 0.1 % уровень (соответственно менее 0.001).
При выбранном уровне значимости a выделяющееся значение x* считают грубой ошибкой и исключают его из дальнейшей обработки результатов измерений, если для соответствующего коэффициента t, рассчитанного по формуле (5.1), выполняется условие: 1 – Ф(t) < a.
Метод исключения при неизвестной s_i.
Если средняя квадратическая ошибка отдельного измерения s_i заранее неизвестна, то она оценивается приближенно по результатам измерений посредством формулы (2.8). Далее применяется тот же алгоритм, что и при известной s_i с той лишь разницей, что в формуле (5.1) вместо s_iиспользуется величина S_n, рассчитанная по формуле (2.8).
Правило трех сигм.
Так как выбор надежности доверительной оценки допускает некоторый произвол, в процессе обработки результатов эксперимента широкое распространение получило правило трех сигм: отклонение истинного значения измеряемой величины не превосходит среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого значения.
Таким образом, правило трех сигм представляет собой доверительную оценку в случае известной величины s
(5.2)
или доверительную оценку
(5.3)
в случае неизвестной величины s.
Первая из этих оценок имеет надежность 2Ф(3) = 0.9973 независимо от количества измерений.
Надежность второй оценки существенно зависит от количества измерений n.
Зависимость надежности р от количества измерений n для оценки грубой ошибки в случае неизвестной величины s указана в
Таблица 4

n
р(х)	0.960	0.970	0.976	0.980	0.983	0.985	0.990	0.993	0.995	0.996	0.997	0.9973

37.Проверка основной гипотезы о нормальном законе распределения данных эксперимента.

Все приведенные выше доверительные оценки как средних значений, так и дисперсий основаны на гипотезе нормальности закона распределения случайных ошибок измерения и поэтому могут применяться лишь до тех пор, пока результаты эксперимента не противоречат этой гипотезе.
Если результаты эксперимента вызывают сомнение в нормальности закона распределения, то для решения вопроса о пригодности или непригодности нормального закона распределения нужно произвести достаточно большое число измерений и применить одну из описанных ниже методик.
Проверка по среднему абсолютному отклонению (САО). Методика может использоваться для не очень больших выборок (n < 120). Для этого вычисляется САО по формуле:
. (4.1)
Для выборки, имеющий приближенно нормальный закон распределения, должно быть справедливо выражение
. (4.2)
Если данное неравенство (4.2) выполняется, то гипотеза нормальности распределения подтверждается.
Проверка по критерию соответствия c² ("хи-квадрат") или критерию согласия Пирсона. Критерий основан на сравнении эмпирических частот с теоретическими, которые можно ожидать при принятии гипотезы о нормальности распределения. Результаты измерений после исключения грубых и систематических ошибок группируют по интервалам таким образом, чтобы эти интервалы покрывали всю ось и чтобы количество данных в каждом интервале было достаточно большим (не менее пяти). Для каждого интервала (х_{i –1}, х_i) подсчитывают число т_iрезультатов измерения, попавших в этот интервал. Затем вычисляют вероятность попадания в этот интервал при нормальном законе распределения вероятностей р_i:
, (4.3)
Далее вычисляют сумму
, (4.4)
где l – число всех интервалов, n – число всех результатов измерений (n = т₁ + т₂ +…+ т_l).
Если сумма, рассчитанная по данной формуле (4.4) окажется больше критического табличного значения c², определяемого при некоторой доверительной вероятности р и числе степеней свободы k = l – 3, то с надежностью р можно считать, что распределение вероятностей случайных ошибок в рассматриваемой серии измерений отличается от нормального. В противном случае для такого вывода нет достаточных оснований.
Проверка по показателям асимметрии и эксцесса. Данный метод дает приближенную оценку. Показатели асимметрии А и эксцесса Еопределяются по следующим формулам:
, (4.5)
. (4.6)
Если распределение нормально, то оба эти показателя должны быть малы. О малости этих характеристик обычно судят по сравнению с их средними квадратическими ошибками. Коэффициенты сравнения рассчитываются соответственно:
, (4.7)
. (4.8)
Распределение можно считать нормальным, если коэффициенты С_А и С_Е не превышают величины 2…3.

38.Корреляция

Корреляция (англ. correlation) в теории вероятностей — зависимость между случайными величинами, не имеющая, вообще говоря, функционального характера; в отличие от функциональной зависимости, как правило, рассматривается тогда, когда одна из величин зависит не только от другой, но и от ряда случайных факторов; проявляется в том, что условное распределение одной случайной величины при фиксированной значении другой отличается от её безусловного распределения. Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанёс пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «увеличение количества пожарных приводит к увеличению причинённого ущерба», и тем более не будет успешной попытка минимизировать ущерб от пожаров путём ликвидации пожарных бригад.^[5] В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет.

39.Коэффициент корреляции, его свойства, корреляционный анализ.

Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

,

где cov(X,Y) — ковариация случайных величин X,Y, а DX,DY — их дисперсии, или, что то же самое, формулой:

,

где и — средние значения (математические ожидания) случайных величин XY,X и Y соответственно.

[редактировать]

Свойства

§ Неравенство Коши — Буняковского:

.

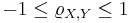§ Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы:

,

где . Более того в этом случае знаки и k совпадают:

.

§ Если X,Y линейно независимые случайные величины, то . Обратное, вообще говоря, неверно.

1. Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации) Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5­­-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.^[13]

2. Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.^[14].

3. Исходная совокупность значений должна быть качественно однородной.^[13]

4. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.^[5]

40.Получение уравнения линейной регрессии с помощью метода наименьших квадратов.
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β, которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции по переменным а и b, приравниваем эти производные к нулю.

Решаем полученную систему уравнений любым методом и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).

При данных а и b функция принимает наименьшее значение.

 

41. Двухпараметрические уравнения нелинейной регрессии.

Выбор вида нелинейной регрессии называется спецификацией или этапом параметризации модели и осуществляется методами визуального оценивания точек корреляционного поля, анализа сути наблюдаемых экономических процессов и т.п. Наиболее часто используют следующие виды нелинейной регрессии:

·
Полиноминальная ;

·
Гиперболическая ;

·
Степенное и т.п.

 

42. Последовательное уточнение уравнения регрессии.

43. Задачи дисперсионного анализа.

Дисперсионный анализ – статистический метод оценки влияния различных факторов на результаты эксперимента. Суть анализа заключается в разложении общей вариации случайной величины на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействие. Факторами обычно называют внешние условия, влияющие на эксперимент.

По числу факторов, влияние которых исследуется, различают:

·
Однофакторный дисперсионный анализ;

·
Двухфакторный дисперсионный анализ;

·
Многофакторный дисперсионный анализ.

Для проведения дисперсионного анализа необходимо соблюдение следующих условий: результаты наблюдений должны быть независимыми случайными величинами с нормальным законом распределения с одинаковой дисперсией.

 

44.Однофакторный дисперсионный анализ. Простейшим случаем дисперсионного анализа является одномерный однофакторный анализ для двух или нескольких независимых групп, когда все группы объединены по одному признаку. В ходе анализа проверяется нулевая гипотеза о равенстве средних. При анализе двух групп дисперсионный анализ тождественен двухвыборочному t-критерию Стьюдента для независимых выборок, и величина F-статистики равна квадрату соответствующей t-статистики.

Для подтверждения положения о равенстве дисперсий обычно применяется критерий Ливена (F-тест). В случае отвержения гипотезы о равенстве дисперсий основной анализ неприменим. Если дисперсии равны, то для оценки соотношения межгрупповой и внутригрупповой изменчивости применятеся F-критерий Фишера:

Если F-статистка превышает критическое значение, то нулевая гипотеза отвергается и делается вывод о неравенстве средних. При анализе средних двух групп результаты могут быть быть интерпретированы непосредственно после применения критерия Фишера.

При наличии трёх и более групп требуется попарное сравнение средних для выявления статистически значимых отличий между ними. Априорный анализ включает метод контрастов, при котором межгрупповая сумма квадратов дробится на суммы квадратов отдельных контрастов:

где есть контраст между средними двух групп, и затем при помощи критерия Фишера проверяется соотношение среднего квадрата для каждого контраста к внутригрупповому среднему квадрату:

Апостериорный анализ включает post-hoc t-критерии по методам Бонферрони или Шеффе, а также сравнение разностей средних по методу Тьюки. Особенностью post-hoc тестов является использование внутригруппового среднего квадрата для оценки любых пар средних. Тесты по методам Бонферрони и Шеффе являются наиболее консервативными, так как они используют наименьшую критическую область при заданном уровне значимости .

Помимо оценки средних, дисперсионный анализ включает определение коэффициента детерминации , показывающего, какую долю общей изменчивости объясняет данный фактор:

 

45. Понятие о двухфакторном дисперсионном анализе.

Двухфакторный анализ проводится аналогично. По каждому фактору вычисляется

своё отношение F и находится своё критическое значение F

α. Отличием схемы двухфак-

торного анализа от однофакторного является то, что в двухфакторном анализе появляется

необходимость проверки гипотезы об отсутствии взаимодействиямежду факторами.