Проверка статистической гипотезы по критерию c2 Пирсона проводится в следующей последовательности:
1. Просматривая полученную по измерениям выборку 
, находят наибольшее – 
и наименьшее – 
значения случайной величины. Разность между наибольшим и наименьшим значениями называется размахом выборки.
2. Найденный размах делится на определенное число интервалов k равной длины, которое рекомендуется выбирать так, чтобы в каждый интервал были бы попадания выборки.
3. Определяется ширина интервала h = 
.
4. Отмечается повторяемость результатов испытания по интервалам, т. е. числа попаданий - 
измеренных значений x в каждый интервал (см. табл.1).
5. По полученной выборке определяются 
- оценки неизвестных параметров теоретического закона распределения. Так как используется нормальный закон распределения, то
, (13)
где:
a = M (x) – математическое ожидание случайной величины х,
2 = D (x) – дисперсия.
Таблица 1
Результаты эксперимента
| № интерв | Нижняя граница интервала | Верхняя граница интервала | Середина интервала | Число попаданий в интервал
| Частота попаданий в интервал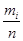 
|
| -7.65 | -6.63 | -7.14 | 0.03 | ||
| -6.63 | -5.61 | -6.12 | 0.08 | ||
| … | … | … | … | … | … |
Статистические оценки математического ожидания – среднее значение ` x и корня квадратного из дисперсии – среднеквадратическое отклонение 
определяются по известным формулам:
= 
, (14)
= 
. (15)
6. Дальнейшие расчеты ведутся с помощью табл. 2, в которой определяются числа попадания в интервалы разбиения (см. табл.1) для случая нормального закона распределения (13) с параметрами, вычисленными в п. 5. Вместо рассмотрения случайной величины 
- середины i - го интервала используется центрированная и нормированная величина 
= 
(см. табл. 2), которая подчиняется нормальному закону распределения с нулевым математическим ожиданием и единичной дисперсией: f(ti) =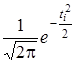 
, где i = 1, 2, …, k. (16)
Этот закон распределения называется функцией Лапласа, значения этой функции могут быть взяты из статистических таблиц (см. табл. П.1.).
.
Таблица 2
Определение числа попаданий в заданные интервалы для нормального закона распределения
| № | Середина интервала xi |
xi -
|
| f(ti) | Вероятность попадания в
интервал
| npi |
| -7.14 | -5.69 | -2.17 | 0.0379 | 0.0144 | 1.44 | |
| -6.12 | -4.67 | -1.78 | 0.0818 | 0.0312 | 3.12 | |
| … | … | … | …. | … | … | … |
В табл. 2 величина pi – вероятность попадания случайной величины x в i –ый интервал подсчитана по приближенной формуле
pi @ 
f(ti).
. 
7. Вычисляется значение 
по формуле (5).
8. Находится число степеней свободы S = k – r - 1,
где r - число параметров в нормальном законе распределения (r = 2).
9. Пользуясь таблицей c2-распределения (см. табл.П.3), по известным значениям S и 
проверяется выполнение критерия (6) и принимается решение о том, согласуются или нет эмпирические и теоретические кривые.
