Эластичность функции.
Эластичностью функции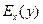 
называется предел отношения относительного приращения функции 
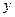к относительному приращению переменной 
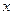при 
:
.
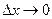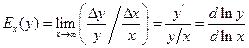Свойства эластичности.
- Эластичность – безразмерная величина.
- Эластичности обратных функций – обратные величины.
- Эластичность произведения двух функций равна сумме эластичностей этих функций.
- Эластичность дроби двух функций равна эластичности числителя минус эластичность знаменателя.
- Эластичность суммы двух функций определяется по формуле:
.
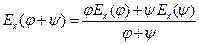Пример 1.
Определить эластичность функции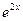 
.
Решение.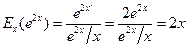 
.
Пример 2.
Определить эластичность функции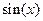 
.
Решение.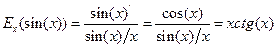 
.
Функции спроса и предложения.
Эластичность может быть использована при анализе спроса и предложения по цене, себестоимости продукции и т.д. Спрос является невозрастающей функцией цены.
Рассмотрим эластичность спроса по цене:
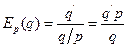, где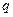 
- функция спроса от цены, 
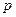- цена товара.
Эластичность спроса по цене показывает, насколько процентов изменится спрос на какой-либо товар при изменении цены товара на один процент и характеризует чувствительность потребителей к изменению цен на товары.
Аналогично определяется эластичность предложения по цене:
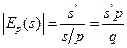, где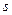 
- количество предлагаемого на продажу товара, 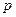- цена товара. Функция 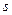является неубывающей функцией от цены.
При равенстве спроса и предложения цена на товар называется равновесной.
Если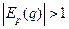 
, то спрос считается эластичным. Если 
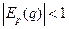, то спрос считается неэластичным.
Выручка продавца (расходы покупателя) рассчитываются по формуле: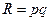 
.
Эластичность выручки по цене определяется как: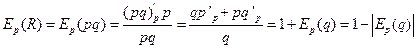 
, поскольку 
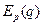всегда отрицательна. Таким образом, если спрос эластичен по цене, то при увеличении цены товара продавец получит меньшую выручку, а при уменьшении – большую. Если спрос неэластичен по цене, выручка возрастет при незначительном увеличении цены на товар и уменьшится при уменьшении цены.
Пример 3.
Функции спроса и предложения имеют вид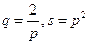 
.
Определить равновесную цену, эластичность спроса и предложения по этой цене, изменение дохода при изменении цены на 3%.
Решение.
Равновесная цена находится из равенства 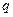= 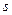или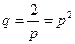 
. Откуда получаем, что 
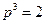или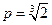 
. Находим эластичности спроса и предложения: 
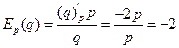и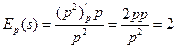 
. Так как полученные эластичности больше 1 по модулю, спрос и предложение эластичны. Уменьшение цены на один процент приводит к увеличению спроса на 2 процента и уменьшению предложения на 2 процента. При увеличении цены на 3% спрос уменьшится на 3*2=6.
Уменьшение дохода равно 6-3=3%.
Пример 4.
Функции спроса и предложения имеют вид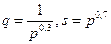 
.
Определить равновесную цену, эластичность спроса и предложения по этой цене, изменение дохода при изменении цены на 3% и изменение выручки продавца при увеличении цены на 1%.
Решение.
Равновесная цена находится из равенства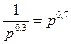 
или 1= . 
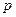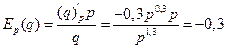
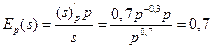. Так как эластичности меньше 1, спрос и предложение неэластичны по цене. При увеличении цены на один процент спрос уменьшится на 0,3 процента. При увеличении цены на 3% доход возрастет на 3-0,9=2,1%. При уменьшении цены на 3% доход уменьшится на 3+0,9=2,1%. Рассчитаем эластичность выручки продавца: 
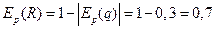. Следовательно при увеличении цены на 1% выручка продавца возрастет на 0,7%.
Задачи для самостоятельного решения.
1. Найти эластичность следующих функций:
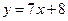
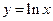
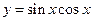
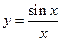
2. Функции спроса и предложения имеют вид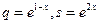 
.
Определить равновесную цену, эластичность спроса и предложения при этой цене, изменение дохода при изменении цены на 3%.
3. Функции спроса и предложения имеют вид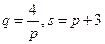 
.
Определить равновесную цену, эластичность спроса и предложения при этой цене, изменение дохода при изменении цены на 3%.
