Пусть функция у = ƒ(х) имеет в точке х отличную от нуля производную:
lim(∆y/∆x) = f’(x) ≠ 0 при ∆x→0. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать ∆y/∆х = ƒ'(х)+α, где α (БМ более высокого порядка, чем ∆x)→0 при ∆х→0, или ∆у = ƒ'(х)*∆х+α*∆х. Дифференциалом функции у = ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): [∆y = ƒ'(х)*∆х] [24.1]. Выясним геометрический смысл дифференциала. Для этого проведем к графику функции у = ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ = ∆х, |AM1| = ∆у. Из прямоугольного треугольника МАВ имеем: tg(α) =|AB|/∆x, т.е. |AB|=tg(α)*∆x. Но, согласно геометрическому смыслу производной, tg(α) = ƒ'(х). Поэтому АВ = ƒ'(х)*∆х. Сравнивая полученный результат с формулой (24.1), получаем dy = АВ, т. е. дифференциал функции у = ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

33 - Применение дифференциала к приближенным вычислениям. Как уже известно, приращение ∆у функции у = ƒ(х) в точке х можно представить в виде ∆у = ƒ'(х)*∆х+α*∆х, где α→0 при ∆х→0, или ∆у = dy+α*∆х. Отбрасывая бесконечно малую α*∆х более высокого порядка, чем ∆х, получаем приближенное равенство [∆у≈dy] [24.3]. Причем это равенство тем точнее, чем меньше ∆х. Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике. Пример. Найти приближенное значение приращения функции у = х3-2х+1 при х = 2 и ∆х = 0,001. Решение. Применяем формулу (24.3): ∆у≈dy = (х3-2х+1)'*∆х = (3х2-2)*∆х. dy|x=2; ∆x=0.001 = (3*4-2)*0.001 = 10*0.001 = 0.01. Итак, ∆у≈0,01. Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем ∆у:
∆у=((х+∆х)3-2(х+∆х)+1)-(х3-2х+1)=х3+3х2*∆х+3х*(∆х)2+(∆х)3-2х-2*∆х+1-х3+2х-1=∆х(3х2+3х*∆х+(∆х)2-2); ∆y|x=2; ∆x=0.001 = 0.001(3*4+3*2*0.001+0.0012-2) = 0.010006. Абсолютная погрешность приближения равна |∆у-dy| = |0,010006-0,011=0,000006. Подставляя в равенство (24.3) значения ∆у и dy, получим ƒ(х+∆х)-ƒ(х)≈ƒ'(х)∆х или [ƒ(х+∆х)≈ƒ(х)+ƒ'(х)*∆х] [24.4]. Формула (24.4) используется для вычислений приближенных значений функций.
34 - Дифференциалы высших порядков. Пусть у = ƒ(х) дифференцируемая функция, а ее аргумент х — независимая переменная. Тогда ее первый дифференциал dy = ƒ'(х)dx есть также функция х; можно найти дифференциал этой функции. Дифференциал от дифференциала функции у = ƒ(х) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d2y или d2ƒ(х). Итак, по определению d2y = d(dy). Найдем выражение второго дифференциала функции у = ƒ(х). Так как dx = ∆х не зависит от х, то при дифференцировании считаем dx постоянным: d2y = d(dy) = d(f'(x)dx) = (ƒ'(х)dx)'*dx = f"(x)dx*dx = f"(x)(dx)2 т. е. [d2y = ƒ"(х)dх2] [24.5]. Здесь dx2 обозначает (dx)2. Аналогично определяется и находится дифференциал третьего порядка.
35 - Теоремы Ролля, Коши, Лагранжа. Теорема 25.1 (Ролль). Если функция ƒ(х) непрерывна на отрезке [а;b], дифференцируема на интервале (а; b) и на концах отрезка принимает одинаковые значения ƒ(а) = ƒ(b), то найдется хотя бы одна точка сє(а;b), в которой производная ƒ'(х) обращается в нуль, т. е. ƒ'(с) = 0. [!] Так как функция ƒ(х) непрерывна на отрезке [а;b], то она достигает на этом отрезке своего наибольшего и наименьшего значений, соответственно, М и m. Если М = m, то функция ƒ(х) постоянна на [a;b] и, следовательно, ее производная ƒ'(х) = 0 в любой точке отрезка [a;b]. Если М ≠ m, то функция достигает хотя бы одно из значений М или m во внутренней точке с интервала (a;b), так как ƒ(a) = ƒ(b).
Пусть, например, функция принимает значение М в точке х = сє(a;b), т. е. ƒ(с) = М. Тогда для всех хє(a;b) выполняется соотношение: [ƒ(с)≥ƒ(х)] [25.1]. Найдем производнуюƒ'(х) в точке х = с: f’(c) = lim((f(c)+ ∆x)-f(c))/∆x) при ∆х→0.
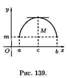
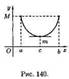
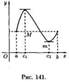
В силу условия (25.1) верно неравенство ƒ(с+∆х)—ƒ(с)≤0. Если ∆х>0 (т. е. ∆х→0 справа от точки х=с), то: (f(c+∆x)-f(c))/∆x≤0 и поэтому ƒ'(с)≤0. Если ∆х<0, то (f(c+∆x)-f(c))/∆x≥0 и ƒ'(с)≥0. Таким образом, ƒ'(с) = 0. В случае, когда ƒ(с) = m, доказательство аналогичное. Геометрически теорема Ролля означает, что на графике функции у = ƒ(х) найдется точка, в которой касательная к графику параллельна оси Ох (см. рис. 139 и 140). На рисунке 141 таких точек две. Теорема 25.2 (Коши). Если функции ƒ(х) и φ(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (α;b), причем φ'(х) ≠ 0 для хє(а;b), то найдется хотя бы одна точка сє(a;b) такая, что выполняется равенство: (f(b)-f(a))/(φ(b)-φ(a)) = f’(c)/φ’(c). Теорема 25.3 (Лагранж). Если функция ƒ(х) непрерывна на отрезке [а;b], ифференцируема на интервале (α;b), то найдется хотя бы одна точка сє(a;b) такая, что выполняется равенство: [ƒ(b)-ƒ(a) = ƒ'(с)(b-a)] [25.2]. Следствие 25.1. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Следствие 25.2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
36 - Правило Лопиталя. Раскрытие неопределённостей различных видов. 36.1 Рассмотрим способ раскрытия неопределенностей вида 0/0 и ∞ /∞, который основан на применении производных. Теорема 25.4 (Правило Лопиталя раскрытия неопределенностей вида 0/0). Пусть функции ƒ(х) и φ(x) непрерывны и дифференцируемы в окрестности точки х0 и обращаются в нуль в этой точке: ƒ(х0) = φ(х0) = 0. Пусть φ'(х) ≠ 0 в окрестности точки х0. Если существует предел: lim(f’(x)/ф’(x) = l, то lim(f(x)/ф(x)) = lim(f’(x)/ф’(x)) = l (всё при х→x0). Теорема 25.5 (Правило Лопиталя раскрытия неопределенностей вида ∞/∞). Пусть функции ƒ(х) и φ(х) непрерывны и дифференцируемы в окрестности точки х0 (кроме, может быть, точки х0). в этой окрестности: lim(f(x)) = lim(ф(x)) = ∞ при х→x0, φ'(х) ≠ 0. Если существует предел: lim(f’(x)/ф’(x), то lim(f(x)/ф(x) = lim(f’(x)/ф’(x) (всё при х→x0). 36.2 Раскрытие неопределенностей различных видов. Правило Лопиталя применяется для раскрытия неопределенностей вида 0/0 и ∞/∞, которые называют основными. Неопределенности вида 0*∞,∞-∞, 1∞, ∞0, 0° сводятся к двум основным видам путем тождественных преобразований. Пусть ƒ(х)→0, φ(х)→ ∞ при х→х0. Тогда очевидны следующие преобразования:
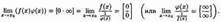
2. Пусть ƒ(х)→ ∞, φ(х)→ ∞ при х→х0. Тогда можно поступить так:
3. Пусть или ƒ(х)→1 и φ(х)→ ∞, или ƒ(х)→ ∞ и φ(x)→0, или ƒ(х)→0 и φ(х)→0 при х→х0. Для нахождения предела вида lim(ƒ(х)φ(х)) при х →х0 удобно сначала прологарифмировать выражение А = ƒ(х)φ(х).
37 - Необходимые и достаточные условия возрастания и убывания функции. Теорема 25.6 (необходимые условия). Если дифференцируемая на интервале (a;b) функция ƒ(х) возрастает (убывает), то ƒ'(х)≥0 (ƒ"(х)≤0) для любого x є (a;b). Теорема 25.7 (достаточные условия). Если функция ƒ(х) дифференцируема на интервале (a;b) и ƒ'(х)>0 (ƒ'(х)<0) для любого xє(a;b), то эта функция возрастает (убывает) на интервале (a;b).
38 - Необходимые и достаточные условия экстремума функции. Теорема 25.8 (необходимое условие экстремума). Если дифференцируемая функция у=ƒ(х) имеет экстремум в точке х0, то ее производная в этой точке равна нулю: ƒ'(х0) = 0. Непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими. Теорема 25.9 (достаточное условие экстремума). Если непрерывная функция у = ƒ(х) дифференцируема в некоторой d -окрестности критической точки х0 и при переходе через нее (слева направо) производная ƒ'(х) меняет знак с плюса на минус, то х0 есть точка максимума; с минуса на плюс, то х0 — точка минимума.
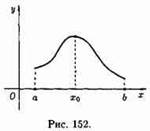
39 - Наибольшее и наименьшее значения функции на отрезке. Пусть функция у = ƒ(х) непрерывна на отрезке [а;b]. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке x0 отрезка [а;b], либо на границе отрезка, т. е. при х0 = а или х0 = b. Если х0є(а;b), то точку х0 следует искать среди критических точек данной функции (см. рис. 152).
Получаем следующее правило нахождения наибольшего и наименьшего значений функции на [а;b]:
1) найти критические точки функции на интервале (а;b);
2) вычислить значения функции в найденных критических точках;
3) вычислить значения функции на концах отрезка, т. е. в точках х = а и х = b;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
40 - Выпуклость графика функции. Точки перегиба. График дифференцируемой функции у = ƒ(х) называется выпуклым вниз на интервале (а;b), если он расположен выше любой ее касательной на этом интервале. График функции у = ƒ(х) называется выпуклым вверх на интервале (а;b), если он расположен ниже любой ее касательной на этом интервале. Точка графика непрерывной функции у = ƒ(х), отделяющая его части разной выпуклости, называется точкой перегиба. На рисунке 154 кривая у = ƒ(х) выпукла вверх в интервале (а;с), выпукла вниз в интервале (с;b), точка М(с;ƒ(с)) — точка перегиба.

Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы. Теорема 25.11. Если функция у = ƒ(х) во всех точках интервала (а;b) имеет отрицательную вторую производную, т. е. ƒ"(х)<0, то график функции в этом интервале выпуклый вверх. Если же ƒ"(х)>0 для любого xє(а;b) — график выпуклый вниз. Теорема 25.12 (достаточное условие существования точек перегиба). Если вторая производная ƒ"(х) при переходе через точку х0, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х0 есть точка перегиба.
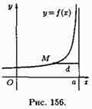
41 - Асимптоты графика функции. Напомним, что асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 156).

Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Говорят, что прямая х = а является вертикальной асимптотой графика функции y = f(x), если lim(f(x)) = ∞ (при x->a) или lim(f(x)) = ∞ (при x->a-0) или lim(f(x)) = ∞ (при x->a+0). Действительно, в этом случае непосредственно из рисунка 156 видно, что расстояние точки М(х;у) кривой от прямой х = а равно d=׀х-а׀. Если х→а, то d→0. Согласно определению асимптоты, прямая х = а является асимптотой кривой у = ƒ(х). Для отыскания вертикальных асимптот нужно найти те значения х, вблизи которых функция ƒ(х) неограниченно возрастает по модулю. Обычно это точки разрыва второго рода. Уравнение наклонной асимптоты будем искать в виде [y = kx+b] [25.5]. Найдем k и b. Пусть М(х;у) — произвольная точка кривой у = ƒ(х) (см. рис. 158). По формуле расстояния от точки до прямой: d = |(Ax0+By0+C)/√(A2+B2)| - находим расстояние от точки М до прямой (25.5): d = |(kx-y+b)/√(k2+1)|. Условие d→0 будет выполняться лишь тогда, когда числитель дроби стремится к нулю, т.е. [lim(kx-y+b) = 0 (при x->∞)] [25.6]. Отсюда следует, что kx-у+b = α, где α = α(х) бесконечно малая: α→0 при х→ ∞. Разделив обе части равенства у=b+kx-α на х и перейдя к пределу при х→ ∞, получаем: lim(y/x) = lim(b/x+k- α/x) (при x->∞). Так как b/х→0 и α/х→0, то [k = lim(y/x) (при x->∞)] [25.7]. Из условия (25.6) находим b: [b = lim(y-kx) (при x->∞)] [25.8]. Итак, если существует наклонная асимптота у = kx+b, то k и b находятся по формулам (25.7) и (25.8). Верно и обратное утверждение: если существуют конечные пределы (25.7) и (25.8), то прямая (25.5) является наклонной асимптотой. Если хотя бы один из пределов (25.7) или (25.8) не существует или равен бесконечности, то кривая у = ƒ(х) наклонной асимптоты не имеет. В частности, если k = 0, то b = limƒ(х) при х →∞. Поэтому у = b — уравнение горизонтальной асимптоты. Замечание: Асимптоты графика функции у=ƒ(х) при х→+ ∞ и х→- ∞ могут быть разными. Поэтому при нахождении пределов (25.7) и (25.8) следует отдельно рассматривать случай, когда х→+∞ и когда х→- ∞.
Формула Тейлора.
Пусть функция ƒ(х) есть многочлен Рn(х) степени n:
ƒ(х)=Рn(х)=а0+а1х+а2х2+...+аnхn. Преобразуем этот многочлен также в многочлен степени n относительно разности х-х0, где х0 — произвольное число, т. е. представим Рn(х) в виде
Рn(х)=А0+A1(x-х0)+А2(х-х0)2+...+Аn(х-х0)n (26.1)
Для нахождения коэффициентов А0, А1,..., Аn продифференцируем n раз равенство (26.1):
Р'n(х)=А1+2А2(х-x0)+3A3(x-x0)2+...+nAn(x-x0)n-1,
Рn''(х)=2*А2+2*3А3(х-х0)+...+n(n-1)Аn(х-х0)n-2,
Рn"'(х)=2*3А3+2*3*4А4(х-х0)+...+n(n-1)(n-2)Аn(х-х0)n-3,
- - - - - - - - - - - - - - - - - -
Рn(n)(х)=n(n-1)(n-2)...2*1*Аn
Подставляя х=х0 в полученные равенства и равенство (26.1), имеем:
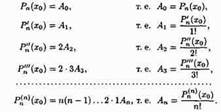
Подставляя найденные значения A0,A1,...,An в равенство (26.1), получим разложение многочлена n-й степени Рn(х) по степеням (х-х0):

Формула (26.2) называется формулой Тейлора для многочлена Рn(х) степени n.






