Концептуальная модель одноуровневого управления потоком заданий в серверной системе

Рис. 3 Концептуальная модель одноуровневого управления потоком заданий в серверной системе

В представленной концептуальной модели отражены два режима работы сервера, в зависимости от размера буферной памяти. Согласно функциональной модели, серверная система производит смену между режимами работы, когда очередь запросов превышает L, соответственно текущий размер буферной памяти при работе в первом режиме равен L, во втором режиме >L.

В зависимости от режима, в котором выполняется работа сервера, интенсивность ответов на клиентские запросы равна - при работе в первом режиме (с буферной памятью L) и - при работе во втором режиме (с буферной памятью >L).

Разработка приложения для определения показателей качества одноуровневого управления потоком заданий в серверной системе

 

Для расчета и сравнительного анализа динамических характеристик систем защиты управления, использующих метод одноуровневого управления используем рассмотренные ранее соотношения (1)-(14). Параметры исследуемых систем заданы в таблице 1.

Табл. 1

Параметры исследуемых систем

	System #1	System #2
Механизм управления	Одноуровневое	Одноуровневое
Параметры управления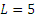

 

где

— интенсивность потока ответов сервера для режима работы с первым сервером;

— интенсивность потока ответов сервера для режима работы со вторым сервером;

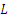— интенсивность входящего потока запросов, при которой выполняется переключение режима работы при одноуровневом управлении;

Параметры и для исследуемых систем отличаются между собой на порядок, что отражает увеличение интенсивности потока ответов.

Интенсивность поступления запросов - изменяемый параметр.

Для оценки динамических характеристик реализуем необходимые функции в среде Matlab.

Функция odnourN(lam, m_1, m_2, L) вычисляет значение – среднее количество запросов, находящихся в системе, при одноуровневом управлении:

 

Рис. 4 Описание функции OdnourN

Функция odnourQ(lam, m_1, m_2, L) вычисляет значение – среднее количество запросов, ожидающих обработки, при одноуровневом управлении:

 

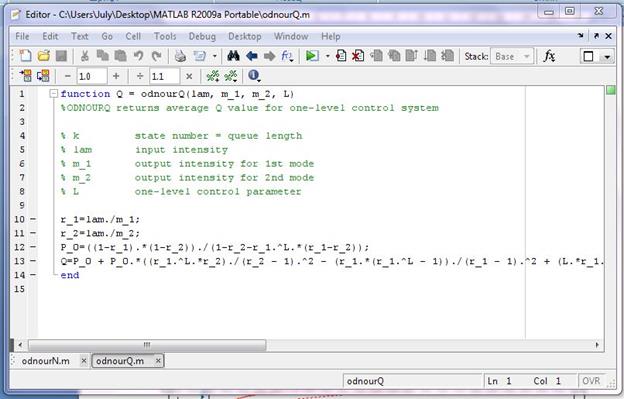
Рис. 5 Описание функции OdnourQ

 

 

Построим графики зависимостей N и Q от входной интенсивности.

Рис. 6 Реализаций функций и построение графиков зависимостей в системе MatLab

 

Графики зависимостей и для исследуемых систем с одноуровневым управлением показаны на рис. 7.

 

Рис. 7 Графики зависимостей среднего количества запросов в системе и среднего количества ожидающих обслуживания запросов от интенсивности входящего потока запросов для двух исследуемых систем с одноуровневым управлением потоком заданий

 

На рис. 7 величины и – характеристики для i -й системы. Из графиков видно, что характеристики и монотонно возрастают с увеличением интенсивности входящего потока .

При 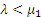длина очереди не превышает порогового значения L для систем с одноуровневым управлением, так как система работает преимущественно с первым сервером. При приближении величины к значению система работает преимущественно со вторым сервером; длина очереди на некотором интервале возрастает слабо, затем неограниченно возрастает. При система уже не в состоянии обработать входящий поток запросов, характеристики и определить нельзя.