Одноуровневое управление потоком заданий в серверной системе
Следующий график описывает режим работы серверной системы с одноуровневым управлением потоком заданий, на котором показана смена между двумя режимами работы сервера:
 |
Рис. 1 Зависимость интенсивности потока ответов сервераμот числа ожидающих обработки или обрабатываемых в данный момент запросов n при одноуровневом управлении
При одноуровневом управлении потоком заданий в серверной системе работа системы представлена двумя режимами:
· Без кеширования (когда длина очереди меньше L)
· С кешированием (Количество запросов к серверу, ожидающих обработки или обрабатываемых в данный момент превышает значение L)
Кеширование - сохранение однажды полученных данных в кеше с целью их повторного использования без обращения к серверу-источнику. Документ, сохраненный в кеше, будет доступен при следующем обращении к нему, без выгрузки с сервера-источника, что помогает повысить скорость доступа клиента к нему.
Параметр L – длина очереди,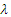 
- интенсивность потока запросов, 
и 
- интенсивности потока ответов сервера для режимов без кеширования и с кешированием соответственно.
Далее изображен граф цепи Маркова, соответствующий рассматриваемому процессу рождения (входящий поток запросов) и гибели (поток ответов сервера). Вершины графа – стационарные вероятности нахождения процесса N(t) в конкретном состоянии, а дуги – интенсивности переходов между состояниями.
 |
Рис. 2 Граф, описывающий переходы между состояниями процесса N(t) с различной длиной очереди при использовании одноуровневого управления
Определение показателей качества функционирования серверной системы с одноуровневым управлением потоком заданий
N(t) - число запросов, находящихся в системе (обрабатываемых в данный момент или ожидающих обработки) в момент времени t, описывается процессом рождения и гибели, где интенсивность рождения равна интенсивности входящего потока запросов от клиента, а интенсивность гибели – интенсивность потока ответов сервера.
- состояния, принимаемые процессом N (t), таким образом, установившиеся (стационарные) вероятности нахождения процесса N (t) в состоянии n вычисляются по формуле 1:
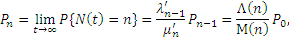
| (1) |
где 
и 
— интенсивности входящего потока запросов и потока ответов сервера соответственно, при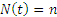 
;
| (2) |
Стационарная вероятность 
вычисляется из того условия, что
| (3) |
Введём обозначения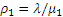 
и 
и предположим, что 
. Из соотношений (1) – (3) следует, что
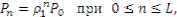
| (4) |
| (5) |
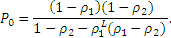
| (6) |
Производящая функция от стационарного распределения длины очереди
| (7) |
Средняя длина очереди, т.е. среднее количество запросов к серверу, находящихся в системе (ожидающих обработки, либо обрабатываемых в данный момент)
| (8) |
В любой момент времени t только один запрос из всех находящихся в системе находится на обработке. Число ожидающих обработки запросов 
связано с количеством всех находящихся в системе запросов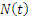 
следующим соотношением:
| (9) |
Следовательно, производящая функция от стационарного распределения числа запросов, ожидающих обработки связана с найденной ранее производящей функцией 
соотношением
| (10) |
Таким образом,
| (11) |
и среднее число ожидающих обработки запросов
| (12) |
Связь между средним временем ответа 
и средним числом находящихся в системе запросов 
задает одна из формул Литтла: 
. Аналогичным соотношением связаны между собой среднее время ожидания 
и среднее число ожидающих обработки запросов: 
Длительность обслуживания позволяет вычислить следующее соотношение:
Время ответа (T) = время ожидания (W) + длительность обслуживания (S).
Исходя из соотношений (6), (8), (12) и формул Литтла, итоговые выражения для искомых параметров выглядят следующим образом:
Среднее время простаивания в очереди при одноуровневом управлении:
| (13) |
среднее время обслуживания при одноуровневом управлении:
| (14) |
где , ,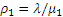
