1.1.  – окрестностью точки А пространства
– окрестностью точки А пространства  называется открытый шар радиуса
называется открытый шар радиуса  с центром в т. А.
с центром в т. А.
1.2. Прямоугольной окрестностью точки является m-мерный параллелепипед
(x10-δ1,x10+ δ 1;x20- δ 2,x20+ δ 2;…;xn0- δ n,xn0+ δ n) с центром в точке M0(x10,x21,…,xn0) а δ 1, δ 2,… δ n – целые наперед заданные числа.
1.3. Окрестностью точки А пространства  называется любое открытое связное множество, содержащее точку А.
называется любое открытое связное множество, содержащее точку А.
1.4. Точка А называется внутренней точкой множества D 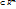 , если
, если 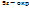 т. А, целиком принадлежащая множеству D.
т. А, целиком принадлежащая множеству D.
1.5. Точка А называется изолированной точкой множества D 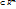 , если
, если 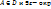 т. А, в которой нет других точек из D, кроме А.
т. А, в которой нет других точек из D, кроме А.
1.6. Точка А называется граничной точкой множества D 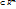 , если в
, если в  – окрестности т. А содержатся точки, как принадлежащие множеству D, так и не принадлежащие ему.
– окрестности т. А содержатся точки, как принадлежащие множеству D, так и не принадлежащие ему.
1.7. Границей множества {M} называется множество всех граничных точек этого множества.
1.8. Множество {М} называется открытым, если все его точки внутренние.
1.9. Множество {М} называется замкнутым, если оно содержит все свои граничные точки.
1.10. Точка А называется предельной точкой множества D 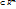 , если
, если 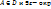 т. А, содержатся точки из D, отличные от А.
т. А, содержатся точки из D, отличные от А.
1.11. Множество {M} называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей {M}.
1.12. Множество точек {М( - некоторые числа, называется прямой в пространстве
- некоторые числа, называется прямой в пространстве  . Эта прямая проходит через точку
. Эта прямая проходит через точку 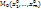
1.13. Множество точек L={М( - непрерывные ф-ии на сегменте
- непрерывные ф-ии на сегменте 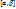 , называется непрерывной кривой в пространстве
, называется непрерывной кривой в пространстве  .
.
Тема 2. Последовательности точек пространства  .
.
1.1. Последовательность {Mn} называется ограниченной, если все ее члены лежат в некотором шаре. (эквивалентное опр.: 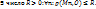 (О – начало коорд))
(О – начало коорд))
1.2. Последовательность {Mn} называется неограниченной, если 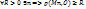 (O – начало коорд.)
(O – начало коорд.)
1.3. Точка А назыв пределом последовательности {Mn}, если 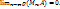
1.4. Последовательность {Mn} называется сходящейся, если последовательность 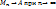 .
.
1.5. Последовательность {Mn} называется фундаментальной, ели 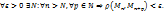
1.6. Точка А называется предельной точкой последовательности точек пространства  - {Mn}, если в любой
- {Mn}, если в любой  – окрестности точки содержатся точки последовательности {Mn}, отличные от А.
– окрестности точки содержатся точки последовательности {Mn}, отличные от А.
2.1. Критерий Коши сходимости последовательности. Для того, чтобы последовательность {Mn} сходилась, необходимо и достаточно, чтобы она была фундаментальной.
2.2. Теорема Больцано-Вейерштрасса. Из любой ограниченной последовательности точек пространства  можно выделить сходящуюся последовательность.
можно выделить сходящуюся последовательность.
Тема 3. Функции, предел, непрерывность.
1.1. Функция u=f(M) называется ограниченной сверху на D, если 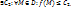
1.2. Функция u=f(M) называется неограниченной сверху на D, если 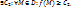
1.3. Функция u=f(M) называется ограниченной снизу на D, если 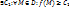 .
.
1.4. Функция u=f(M) называется неограниченной снизу на D, если 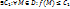
1.5. Число U называется точной верхней грань ю ф-ии u=f(M) на множестве {M}, если: 1) 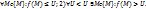
1.6. Число U называется точной нижней грань ю ф-ии u=f(M) на множестве {M}, если: 1) 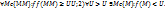
1.7. (По Коши). Число b называется пределом функции f (M) в точке А (при М  А), если
А), если 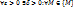 удовлетворяющей условию
удовлетворяющей условию 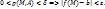
1.8. (По Гейне). Число b называется пределом функции f (M) в точке А, если для любой сходящейся к А последовательности {Мn} такой, что Мnє{М}, Мn  А, соответствующая последовательность значений функции {f(Mn }) сходится к b.
А, соответствующая последовательность значений функции {f(Mn }) сходится к b.
1.9 .(По Гейне) Число b называется пределом функции u=f(M) при M→  , если для любого положительного числа ε можно указать такое положительное число а, что для всех M из области задания функции, удовлетворяющих условию ρ(O,M)>a, выполняется неравенство |f(M)-b|<ε
, если для любого положительного числа ε можно указать такое положительное число а, что для всех M из области задания функции, удовлетворяющих условию ρ(O,M)>a, выполняется неравенство |f(M)-b|<ε
1.10. (По Коши). Число в называется пределом ф-ии u=f(M) при M 
1.11. Функция u=f(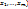 называется непрерывной в точке А(
называется непрерывной в точке А( 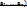 по переменной
по переменной  , если
, если  . (… если ф-я f(
. (… если ф-я f(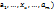 одной переменной
одной переменной  непрерывна в т.
непрерывна в т. 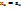 .
.
1.12. Функция u=f( называется непрерывной в точке А по совокупности переменных, если
называется непрерывной в точке А по совокупности переменных, если 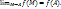
1.13. Функция u=f( называется непрерывной на множестве {M}, если она непрерывна в каждой точке этого множества.
называется непрерывной на множестве {M}, если она непрерывна в каждой точке этого множества.
2.1. (по Коши). Число b называется пределом функции f(M) в точке А (при М -> А), если 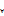 ε > 0 3δ > 0 такое, что
ε > 0 3δ > 0 такое, что 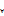 M, удовлетворяющей условиям М є {М}, 0 < ρ(М, А) < δ, выполняется неравенство |f(М) – b| < ε.
M, удовлетворяющей условиям М є {М}, 0 < ρ(М, А) < δ, выполняется неравенство |f(М) – b| < ε.
2.2. Теорема о непрерывности суммы 2-ух непрерывных ф-ий. Если функции f(M) и g(М) определены на множестве {М} и непрерывны в точкеAє{М}, то функция f(M)+g(M), непрерывна в точке А
2.3. Теорема о непрерывности произведения 2-ух непрерывных ф-ий. Если функции f(M) и g(М) определены на множестве {М} и непрерывны в точке Aє{М}, то функция f(M)*g(M), непрерывна в точке А.
2.4. Теорема о непрерывности частного 2-ух непрерывных ф-ий. Если функции f(M) и g(М) определены на множестве {М} и непрерывны в точке Aє{М}, причем ф-я g(М) 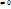 , то функция f(M)/g(M), непрерывна в точке А.
, то функция f(M)/g(M), непрерывна в точке А.
2.5. Теорема о прохождении непрерывной ф-ии через любое промежуточное значение. Пусть функция u=f(M)= 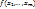 непрерывна во всех точка связного множества {M}, пусть
непрерывна во всех точка связного множества {M}, пусть 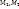 - две любые точки из {M}, f(M1)=u1, f(M2)=u2и пусть u0 – любое число из сегмента [u1,u2]. Тогда на любой непрерывной кривой L, соединяющей точки
- две любые точки из {M}, f(M1)=u1, f(M2)=u2и пусть u0 – любое число из сегмента [u1,u2]. Тогда на любой непрерывной кривой L, соединяющей точки 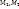 и целиком
и целиком 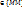 , найдется точка М0 такая, что f(M0)=u0.
, найдется точка М0 такая, что f(M0)=u0.
2.6. Первая теорема Вейерштрасса. Непрерывная на замкнутом ограниченном множестве функция ограничена на этом множестве.
2.7. Вторая теорема Вейерштрасса. Непрерывная на замкнутом ограниченном множестве функция достигает на этом множестве своих точных граней.
2.8. Теорема о непрерывности сложной ф-ии нескольких переменных. Пусть ф-ии 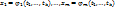 , непрерывны в точке А(
, непрерывны в точке А(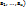 , а ф-я
, а ф-я 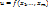 непрерывна в точке В(
непрерывна в точке В(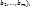 где
где 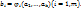 Тогда сложная ф-я u=
Тогда сложная ф-я u= 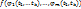 непрерывна в т. А.
непрерывна в т. А.
2.9. Теорема Кантора для ф-ии нескольких переменных. Непрерывная на замкнутом ограниченном множестве ф-я равномерно непрерывна на этом множестве.
4.1. Теорема о непрерывности суммы 2-ух непрерывных ф-ий. Если функции f(M) и g(М) определены на множестве {М} и непрерывны в точкеAє{М}, то функция f(M)+g(M), непрерывна в точке А. (т.к. функции f(M) и g(М) непрерывны в точке А, то они в этой точке имеют предельные значения, тогда существует предельное значение ф-ии f(M)+g(M)существует и равно f(A)+g(A), но эта величина равна частному значению данной ф-ии. Ч.т.д.)
4.2. Теорема о непрерывности произведения 2-ух непрерывных ф-ий. Если функции f(M) и g(М) определены на множестве {М} и непрерывны в точке Aє{М}, то функция f(M)*g(M), непрерывна в точке А. (т.к. функции f(M) и g(М) непрерывны в точке А, то они в этой точке имеют предельные значения, тогда существует предельное значение ф-ии f(M)*g(M)существует и равно f(A)*g(A), но эта величина равна частному значению данной ф-ии. Ч.т.д.)
4.5. Теорема о прохождении непрерывной ф-ии через любое промежуточное значение. Пусть функция u=f(M)= 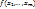 непрерывна во всех точка связного множества {M}, пусть
непрерывна во всех точка связного множества {M}, пусть 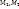 - две любые точки из {M}, f(M1)=u1, f(M2)=u2и пусть u0 – любое число из сегмента [u1,u2]. Тогда на любой непрерывной кривой L, соединяющей точки
- две любые точки из {M}, f(M1)=u1, f(M2)=u2и пусть u0 – любое число из сегмента [u1,u2]. Тогда на любой непрерывной кривой L, соединяющей точки 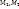 и целиком
и целиком 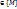 , найдется точка М0 такая, что f(M0)=u0. (Пусть L={M(
, найдется точка М0 такая, что f(M0)=u0. (Пусть L={M(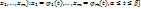 – непрерывная кривая, соединяющая точки
– непрерывная кривая, соединяющая точки 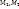 и целиком
и целиком 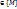 , в частности,
, в частности, 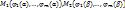 . На кривой L:
. На кривой L: 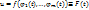 причем ф-я F(t) непрерывна на [
причем ф-я F(t) непрерывна на [ 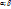 ],
],  В силу теоремы для ф-ии одной переменной
В силу теоремы для ф-ии одной переменной 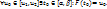 Но
Но 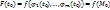 , где т.
, где т. 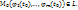 Итак,
Итак, 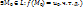
4.6. Первая теорема Вейерштрасса. Непрерывная на замкнутом ограниченном множестве функция ограничена на этом множестве. (Допустим, что u=f(M) не ограничена на {M}. Тогда 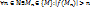 . Т.е.
. Т.е. 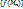 - бесконечно большая. Изогранич. послед.
- бесконечно большая. Изогранич. послед. 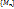 можно выделить сходящуюся послед. Пусть
можно выделить сходящуюся послед. Пусть 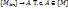 . Поэтому функция f(M) непрерывна в т. А. Следовательно
. Поэтому функция f(M) непрерывна в т. А. Следовательно 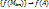 , а это противоречит тому, что
, а это противоречит тому, что 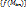 - бесконечно большая. Ч.т.д.)
- бесконечно большая. Ч.т.д.)
4.7. Вторая теорема Вейерштрасса. Непрерывная на замкнутом ограниченном множестве функция достигает на этом множестве своих точных граней. (докажем, что функция f(x) достигает на множестве {M} своей точной верхней грани К (нижняя аналогично). От противного. Функция ни в одной точке множества не равна К, тогда для всех точек множества справедливо f(x)<K и можно рассмотреть на множестве всюду положительную ф-ю F(x)=1/(K-f(x)). Т.к. знаменатель 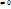 и непрерывен на множестве{M}, то ф-я также непрерывна на множестве {M} => ф-я ограничена на множестве {M}, т.е. найдется положительное число В:
и непрерывен на множестве{M}, то ф-я также непрерывна на множестве {M} => ф-я ограничена на множестве {M}, т.е. найдется положительное число В: 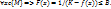 Последнее неравенство перепишем так: f(x)
Последнее неравенство перепишем так: f(x) 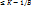 . Это справедливо для всех х из {M}, что противоречит тому, что К-точная верхняя грань (наименьшая из всех верхних граней) функции на множестве. Ч.т.д.)
. Это справедливо для всех х из {M}, что противоречит тому, что К-точная верхняя грань (наименьшая из всех верхних граней) функции на множестве. Ч.т.д.)
Тема 4. Дифференцируемые функции.
1.1. Частной производной ф-ииu=f(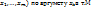 называется
называется 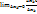 . (Если он существует)
. (Если он существует)
1.2. Функция u=f(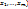 называется дифференцируемой в т. М (
называется дифференцируемой в т. М (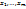 ), если ее полное приращение в этой точке можно представить в виде
), если ее полное приращение в этой точке можно представить в виде 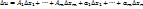 , где
, где  –некоторые числа,
–некоторые числа, 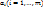 –функции аргументов
–функции аргументов 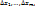 бесконечно малые при
бесконечно малые при 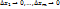 и равные нулю при
и равные нулю при 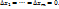
1.3. Первым дифференциалом ф-ииu=f(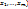 в точке М называется линейная функция аргументов
в точке М называется линейная функция аргументов 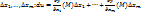
1.4. Плоскость Р, проходящая через точку N0 поверхности S, называется касательной плоскостью к поверхности S в этой точке, если при 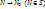 величина
величина 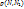 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 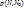 , т.е.
, т.е. 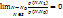 .
.
1.5. Функция u=f(x1,…,xm) называется дифференцируемой n раз в точке М0, если все ее частные производные (n-1) порядка дифференцируемы в этой точке.
1.6. Второй дифференциал d2u ф-ии u(x,y) в точке М0 определяется как дифференциал в т. М0 от первого дифференциала du при следующих условиях: 1) du рассматривается только как ф-я независимых переменных х и у; 2)при вычислении дифференциалов от 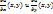 приращения независимых переменных х и у берутся такими же, как и в выражении для du, т.е. равными dx и dy. (
приращения независимых переменных х и у берутся такими же, как и в выражении для du, т.е. равными dx и dy. ( .
.
1.7. N-ый дифференциал dnu ф-ии u(x,y) в точке М0 определяется как дифференциал в т. М0 от (n-1) дифференциала при следующих условиях: 1) du рассматривается только как ф-я независимых переменных х и у; 2)при вычислении дифференциалов от 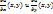 приращения независимых переменных х и у берутся такими же, как и в выражении для dn-1u, т.е. dnu=d(dn-1u).
приращения независимых переменных х и у берутся такими же, как и в выражении для dn-1u, т.е. dnu=d(dn-1u).
1.8. Функция u=f(x,y,z) является сложной функцией одной переменной величины l. Если эта функция имеет в точке l = 0 производную по переменной l, то эта производная называется производной по направлению от функции u=f(x,y,z) в точке M0 и обозначается символом ∂u/∂l. (x=x0 + lcosα, y=y0 + lcosβ, z=z0 + lcosγ). [Если 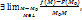 то он называется производной ф-ииu=f(M) в т. Мо по направлению
то он называется производной ф-ииu=f(M) в т. Мо по направлению  и обозначается
и обозначается 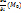 ]
]
1.9. Градиентом дифференцируемой функции u=f(x,y,z) в точке Мo называется вектор следующего вида grad u= 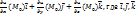 - единичные векторы осей координат.
- единичные векторы осей координат.
2.1. Необходимое условие дифференцируемости ф-ии. Если ф-я u=f(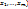 дифференцируема в т. М(
дифференцируема в т. М(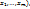 то она имеет в т. М частные производные по всем переменным.
то она имеет в т. М частные производные по всем переменным.
2.2. Д остаточное условие дифференцируемости ф-ии. Если ф-яu=f(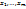 ) имеет частные производные по всем переменным в некоторой
) имеет частные производные по всем переменным в некоторой  - окрестности т. М(
- окрестности т. М(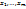 ), причем в самой т. М эти частные производные непрерывны, то ф-я дифференцируема в т.М.
), причем в самой т. М эти частные производные непрерывны, то ф-я дифференцируема в т.М.
2.3. Достаточные условия равенства смешанных производных. Если в некоторой окрестности точки М0(х0, у0) ф-я u=f(x,y) имеет смешанные частные производные fxy(x,y) и fyx(x,y), причем эти смешанные частные производные непрерывны в точке М0, то они равны в этой точке: fxy(x0,y0)= fyx(x0,y0).
2.4. Теорема о касательной плоскости к гр-ку ф-ии. Если ф-я u=f(x,y) дифференцируема в т. М0(х0,у0), то в точке N0(x0,y0,f(x0,y0)) существует касательная плоскость к поверхности S (гр-ку этой ф-ии), причем уравнение касательной плоскости имеет вид 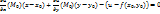 .
.
2.5. Tеорема о дифференцируемости сложной ф-ии. Пусть1) функции x=φ(u,v), y=  (u,v) дифференцируемы в некоторой точке(
(u,v) дифференцируемы в некоторой точке(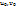 ), 2) функция z=f(x,y), дифференцируема в соответствующей точке(
), 2) функция z=f(x,y), дифференцируема в соответствующей точке(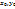 ), где x0=φ(
), где x0=φ(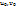 ), y0=
), y0=  (
(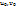 ). Тогда сложная функция z=f(φ(u,v),
). Тогда сложная функция z=f(φ(u,v),  (u,v)), дифференцируема в точке (
(u,v)), дифференцируема в точке (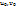 ).
).
2.6. Частная производная сложной ф-ии. 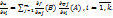
2.7.Выражение производной функции f(x,y.z) по заданному направлению в данной точке через частные производные производные в этой точке 
2.8. Выражение производной функции f(x,y.z) по заданному направлению в данной точке через градиент функции в этой точке 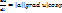
2.9. Формула Лагранжа.  (при n=0 из формулы:
(при n=0 из формулы: 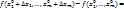 du
du 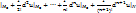 ).
).
2.10. Второй дифференциал.  .
.
2.11. N дифференциал. 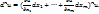
2.13. Формула Тейлора (Лагранж). Если ф-я u=f(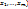 (n+1) – раз диффер. в некоторой -окрестности т.
(n+1) – раз диффер. в некоторой -окрестности т. 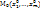 , то
, то 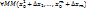 из этой
из этой  -окрестности приращения ф-ии
-окрестности приращения ф-ии  , где N- некоторая точка, лежащая на отрезке
, где N- некоторая точка, лежащая на отрезке 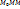 , а дифференциалы
, а дифференциалы 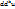 вычисляются по формуле:
вычисляются по формуле: 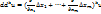 .
.
2.14. Формула Тейлора (Пеано). Пусть n 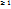 - целое число, ф-я u=f(M)=f(
- целое число, ф-я u=f(M)=f(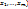 (n+1) – раз диффер. в некоторой -окрестности т.
(n+1) – раз диффер. в некоторой -окрестности т. 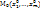 и n раз дифференцируема в самой точке М0, то
и n раз дифференцируема в самой точке М0, то 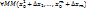 из этой
из этой  -окрестности приращения ф-ии
-окрестности приращения ф-ии  , где
, где 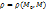 – расстояние, а
– расстояние, а 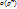 – бесконечно малая при
– бесконечно малая при 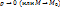 ф-ю более высокого порядка малости, чем
ф-ю более высокого порядка малости, чем  .
.
4.1. Необходимое условие дифференцируемости ф-ии. Если ф-я u=f(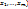 дифференцируема в т. М(
дифференцируема в т. М(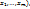 то она имеет в т. М частные производные по всем переменным. (По условию дифференцируемости
то она имеет в т. М частные производные по всем переменным. (По условию дифференцируемости 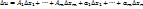 , где
, где  –некоторые числа,
–некоторые числа, 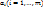 –функции аргументов
–функции аргументов 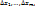 бесконечно малые при
бесконечно малые при 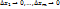 и равные нулю при
и равные нулю при 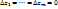 . Положим все
. Положим все 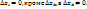 Тогда
Тогда  Отсюда
Отсюда 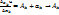 при
при 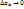 , т.е.
, т.е. 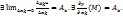 Ч.т.д.)
Ч.т.д.)
4.2. Достаточное условие дифференцируемости ф-ии. Если ф-яu=f(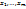 ) имеет частные производные по всем переменным в некоторой
) имеет частные производные по всем переменным в некоторой  - окрестности т. М(
- окрестности т. М(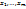 ), причем в самой т. М эти частные производные непрерывны, то ф-я дифференцируема в т.М. (Док-во приведем для ф-ии 2 переменных (для сокращения). Пусть частные производные
), причем в самой т. М эти частные производные непрерывны, то ф-я дифференцируема в т.М. (Док-во приведем для ф-ии 2 переменных (для сокращения). Пусть частные производные 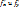 существуют в
существуют в  - окрестности т. М(х,у) и непрер. в самой т. М. Возьмем
- окрестности т. М(х,у) и непрер. в самой т. М. Возьмем 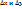 столь малыми, чтобы т.
столь малыми, чтобы т. 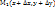 лежала в этой
лежала в этой  - окрестности т. М.
- окрестности т. М.  где
где 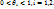 Т.к.
Т.к. 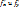 непрер. в т. М(x,y), то
непрер. в т. М(x,y), то  Следовательно
Следовательно  , т.е. выполняется условие дифференцируемости)
, т.е. выполняется условие дифференцируемости)
4.5. Сформулируйте и докажите теорему о дифференцируемости сложной ф-ии. Пусть1) функции x=φ(u,v), y=  (u,v) дифференцируемы в некоторой точке(
(u,v) дифференцируемы в некоторой точке(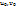 ), 2) функция z=f(x,y), дифференцируема в соответствующей точке(
), 2) функция z=f(x,y), дифференцируема в соответствующей точке(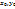 ), где x0=φ(
), где x0=φ(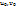 ), y0=
), y0=  (
(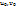 ). Тогда сложная функция z=f(φ(u,v),
). Тогда сложная функция z=f(φ(u,v),  (u,v)), дифференцируема в точке (
(u,v)), дифференцируема в точке (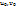 ). (Дадим произвольные приращения
). (Дадим произвольные приращения 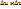 аргументам u и v в т.(
аргументам u и v в т.(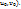 Ф-ииx=φ(u,v), y=
Ф-ииx=φ(u,v), y=  (u,v) получат приращения
(u,v) получат приращения 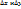 , которые можно представить в виде
, которые можно представить в виде  где
где 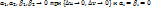 при
при 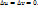 Этим приращениям
Этим приращениям 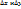 соответствует некоторое приращение
соответствует некоторое приращение  ф-ииz=f(x,y)в точке(
ф-ииz=f(x,y)в точке(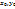 ), котороеможнозаписать:
), котороеможнозаписать: 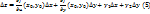 , где
, где  . Подставим (4) –> (5):
. Подставим (4) –> (5):  , где
, где 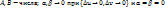 при
при  . Значит сложнаяфункция z=f(φ(u,v),
. Значит сложнаяфункция z=f(φ(u,v),  (u,v)), дифференцируема в точке (
(u,v)), дифференцируема в точке (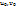 ). Ч.т.д.)
). Ч.т.д.)
4.7. Формула Тейлора. Если ф-я u=f(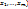 (n+1) – раз диффер. в некоторой -окрестности т.
(n+1) – раз диффер. в некоторой -окрестности т. 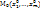 , то
, то 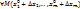 из этой
из этой  -окрестности приращения ф-ии
-окрестности приращения ф-ии  , где N- некоторая точка, лежащая на отрезке
, где N- некоторая точка, лежащая на отрезке 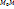 , а дифференциалы
, а дифференциалы 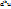 вычисляются по формуле:
вычисляются по формуле: 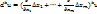 . (Зафиксируем точку М
. (Зафиксируем точку М 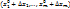 . Уравнения отрезка
. Уравнения отрезка 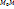 можно записать в виде
можно записать в виде  . На отрезке
. На отрезке 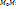 u=f(
u=f(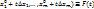 - сложная ф-я одной переменной t, причем она (n+1)-раз дифференцируема на отрезке
- сложная ф-я одной переменной t, причем она (n+1)-раз дифференцируема на отрезке 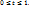 Заметим, что
Заметим, что  . Т.к.
. Т.к. 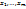 – линейные ф-ииt, то диф-лы
– линейные ф-ииt, то диф-лы 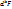 можно вычислить:
можно вычислить:  (3):
(3): 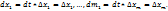 Итак,
Итак,  Подставляя (6), (7) в (5) и учитывая (4), получаем формулу (2). Ч.т.д.)
Подставляя (6), (7) в (5) и учитывая (4), получаем формулу (2). Ч.т.д.)
Тема 5. Локальный экстремум.
1.1. Говорят, что ф-я u=f(M) имеет в т.  локальный максимум (минимум), если существует такая -окрестности т.
локальный максимум (минимум), если существует такая -окрестности т.  , в которой
, в которой 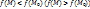 при
при 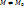
2.1. Необходимое условие экстремума (диф ф-ии). Если в т. 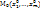 ф-я u=f(
ф-я u=f(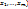 имеет локальный экстремум и если в т.
имеет локальный экстремум и если в т. 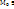 существует частная производная
существует частная производная 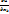 , то
, то 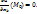
2.2. Достаточное условие экстремума (дважды диф. ф-ии). Пусть ф-я u=f(M)=f(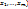 ифференцируема в некоторой окрестности точки
ифференцируема в некоторой окрестности точки 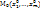 и дважды дифференцируема в самой точке М0, причем М0 – точка возможного экстремума данной ф-ии, т.е.
и дважды дифференцируема в самой точке М0, причем М0 – точка возможного экстремума данной ф-ии, т.е. 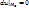 . Тогда если второй дифференциал
. Тогда если второй дифференциал 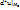 является положительно определенной (отрицательно определенной) квадратичной формой от переменных dx1,…,dxm, то ф-я u=f(M) имеет в т. М0 локальный минимум (максимум). Если же
является положительно определенной (отрицательно определенной) квадратичной формой от переменных dx1,…,dxm, то ф-я u=f(M) имеет в т. М0 локальный минимум (максимум). Если же 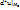 является знакопеременной квадратичной формой, то в точке М0 ф-я u=f(M) не имеет локального экстремума.
является знакопеременной квадратичной формой, то в точке М0 ф-я u=f(M) не имеет локального экстремума.
4.1. Необходимое условие экстремума. Если в т. 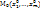 ф-я u=f(
ф-я u=f(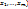 имеет локальный экстремум и если в т.
имеет локальный экстремум и если в т. 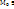 существует частная производная
существует частная производная 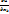 , то
, то 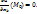 (Зафиксируем все аргументы кроме
(Зафиксируем все аргументы кроме  , положив
, положив 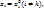 и рассмотрим ф-ю одной переменной
и рассмотрим ф-ю одной переменной 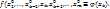 Эта ф-я имеет локальный экстремум в т.
Эта ф-я имеет локальный экстремум в т. 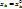 и имеет производную в т.
и имеет производную в т. 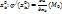 . По теореме о необходимом условии экстремума для ф-ии одной переменной
. По теореме о необходимом условии экстремума для ф-ии одной переменной 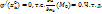 )
)
Тема 6. Неявные функции.
1.1. Функция, заданная таким способом: y=f(x) [или y=f(x1, x2,…,xm)] называется неявной ф-ей и является решением уравнения F(x,y)=0 [или F(x1, x2,…,xm,y)=0]относительно у (т.е. 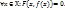 [или F(x1, x2,…,xm, f(x1, x2,…,xm))=0])
[или F(x1, x2,…,xm, f(x1, x2,…,xm))=0])
1.3. Функции 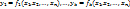 называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция
называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция 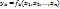 называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде:
называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде: 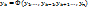 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
1.4. Функции 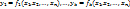 называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция
называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция 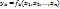 называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде:
называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде: 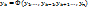 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
2.1. Теорема о существовании и непрерывности ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть 1) ф-я F(x,y) непрерывна в прямоугольнике Q={(x,y):a<x<b, c 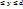 }; 2)
}; 2) 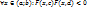 (т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3)
(т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3) 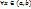 ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
2.2. Теорема о дифференцируемости ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть: 1)ф-я F(x,y) дифференцируема в некоторой окрестности W точки Мо(х0,у0); 2) частная производная Fy непрерывна в точке Мо; 3)F(x0,y0)=0, 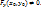 Тогда существует такой прямоугольник
Тогда существует такой прямоугольник 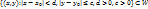 , в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (
, в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (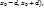 и ее производная вычисляется по формуле
и ее производная вычисляется по формуле 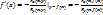 .
.
2.5. Теорема о существовании и дифференцируемости ф-ий y и z, заданных неявно сисемой. Пусть 1)ф-ии F и G, входящие в систему, дифференцируемы в некоторой окрестности W точки 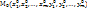 ; 2) частные производные
; 2) частные производные 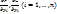 непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0,
непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0, 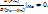 Тогда существует такой параллелепипед
Тогда существует такой параллелепипед  , в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при
, в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при 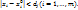
2.6. Теорема о достаточных условиях независимости ф-ии.
Пусть ф-ии 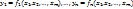 , где n
, где n  m, дифференцируемы в некоторой окрестности
m, дифференцируемы в некоторой окрестности  точки
точки 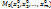 и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в
и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в  .
.
2.7. Теорема о зависимости и независимости ф-ий.
Пусть: 1) ф-ии 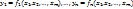 дифференцируемы в окрестности
дифференцируемы в окрестности  точки
точки 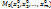 , а частные производные
, а частные производные 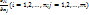 непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий
непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий 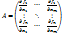 ) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
Тогда r ф-ий, представленных в указанном миноре r-го порядка, независимы в w, а каждая из остальных ф-ий зависит в некоторой окрестности т. М0 от этих r ф-ий.
Тема 8. Кратные интегралы.
1.1. Плоская фигура называется квадрируемой, если точная верхняя грань  множества площадей всех вписанных многоугольных фигур равна точной нижней грани
множества площадей всех вписанных многоугольных фигур равна точной нижней грани 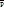 множества площадей всех описанных многоугольных фигур.
множества площадей всех описанных многоугольных фигур.
1.2. Площадь криволинейной трапеции. 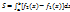 , [ограничена непрерывными кривыми y=f1(x), y=f2(x), a
, [ограничена непрерывными кривыми y=f1(x), y=f2(x), a 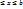 (где
(где 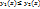 , и двумя отрезками прямых х=а, x=b.]
, и двумя отрезками прямых х=а, x=b.]
1.3. Сумма 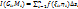 называется интегральной суммой ф-ии f(x,y), где G – квадрируемая область; u=f(M)=f(x,y) – ограниченная ф-я, определенная на G; Gi (i=
называется интегральной суммой ф-ии f(x,y), где G – квадрируемая область; u=f(M)=f(x,y) – ограниченная ф-я, определенная на G; Gi (i= 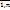 ) – разбиение области G, такое что 2 любые части не имеют общих внутренних точек;
) – разбиение области G, такое что 2 любые части не имеют общих внутренних точек; 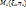 – произвольная точка в Gi.
– произвольная точка в Gi.
1.4. Число I называется пределом интегральных сумм 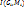 при d -> 0, если
при d -> 0, если 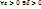 такое, что для любого разбиения области G, у которого d<
такое, что для любого разбиения области G, у которого d<  , и для любого выбора промежуточных точек Mi выполняется неравенство |
, и для любого выбора промежуточных точек Mi выполняется неравенство | 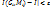 .
.
2.1. Теорема о сведении двойного интеграла к повторному.
Пусть: 1)  двойной интеграл
двойной интеграл 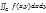 ; 2)
; 2) 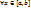 существует определенный интеграл
существует определенный интеграл 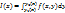 . Тогда существует определенный интеграл
. Тогда существует определенный интеграл 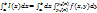 (он называется повторным)и справедливо равенство
(он называется повторным)и справедливо равенство 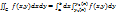 , т.е. двойной интеграл равен повторному.
, т.е. двойной интеграл равен повторному.
2.2. Теорема о формуле для замены переменной в двойном интеграле.
Пусть g и G – замкнутые квадрируемые области, функция f(x,y) ограничена в области G и непрерывна всюду, кроме, быть может, некоторого множества точек площади нуль, а отображение 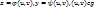 удовлетворяет условиям:1)отображение взаимно однозначное; 2) ф-ии
удовлетворяет условиям:1)отображение взаимно однозначное; 2) ф-ии 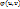 и
и 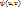 имеют в области g непрерывные частные производные первого порядка; 3) якобиан отображения
имеют в области g непрерывные частные производные первого порядка; 3) якобиан отображения 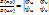 отличен от нуля во всех точках области g. Тогда справедливо равенство:
отличен от нуля во всех точках области g. Тогда справедливо равенство: 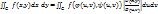 .
.
2.3. Теорема о сведении тройного интеграла к повторному.
Пусть 1) Существует тройной интеграл 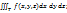 2)
2) 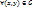 существует определенный интеграл
существует определенный интеграл 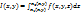 . Тогда существует двойной интеграл
. Тогда существует двойной интеграл 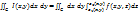 (он называется повторным и справедливо равенство
(он называется повторным и справедливо равенство 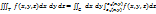 , т.е. тройной интеграл равен повторному.
, т.е. тройной интеграл равен повторному.
2.4. Теорема о формуле замены переменных для тройного интеграла.
Пусть  и Т – замкнутые кубируемые области, ф-я f(x,y,z) ограничена в области Т и непрерывна всюду, кроме, быть может, некоторого множества точек объема 0, а отображение
и Т – замкнутые кубируемые области, ф-я f(x,y,z) ограничена в области Т и непрерывна всюду, кроме, быть может, некоторого множества точек объема 0, а отображение 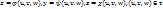 удовлетворяет условиям: 1) отображение взаимнооднозначно; 2)ф-ии
удовлетворяет условиям: 1) отображение взаимнооднозначно; 2)ф-ии 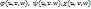 имеют в области
имеют в области  непрерывные частные производные первого порядка; 3) Якобиан отображения
непрерывные частные производные первого порядка; 3) Якобиан отображения 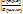 отличен от 0 в области
отличен от 0 в области  . Тогда справедливо равенство:
. Тогда справедливо равенство: 
2.5. Масса и координаты центра тяжести. 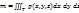
. 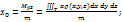
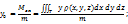
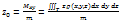 , где
, где 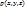 – плотность, Т – материальное тело.
– плотность, Т – материальное тело.
2.6. Моменты инерции плоской фигуры.

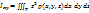 - относительно координатных плоскостей Oyz, Ozx, Oxy.
- относительно координатных плоскостей Oyz, Ozx, Oxy.
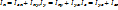 – относительно осей координат Ох, Оy, Oz.
– относительно осей координат Ох, Оy, Oz.
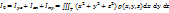 - относительно начала координат.
- относительно начала координат.
Тема 7 Условный экстремум1,1 Говорят, что функция 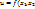 ,..,
,.., 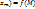 имеет в точке
имеет в точке  условный минимум(максимум) при условиях связи
условный минимум(максимум) при условиях связи 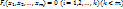 , если существует такая окрестность точки
, если существует такая окрестность точки 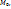 что для любой точки
что для любой точки 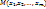
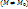 этой окрестности, координаты которой удовлетворяют уравнениям
этой окрестности, координаты которой удовлетворяют уравнениям 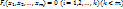 , выполняется неравенство
, выполняется неравенство 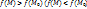 )
)
1,2 Задача об условном экстремуме функции 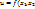 ,..,
,.., 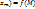 при условиях связи
при условиях связи 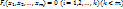 эквивалентна задаче об условном экстремуме функции Лагранжа
эквивалентна задаче об условном экстремуме функции Лагранжа 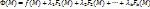 (
(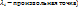 при тех же условиях связи,поскольку в точке M, удовлетворяющих уравнениям связи, справедливо равенство Ф(M)=f(M).
при тех же условиях связи,поскольку в точке M, удовлетворяющих уравнениям связи, справедливо равенство Ф(M)=f(M).
2.1 Необходимые условия Лагранжа условного экстремума. Пусть:1) Функция 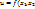 ,..,
,.., 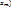 дифференцируема в точке
дифференцируема в точке 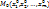 и имеет в этой точке условный экстремум при условиях связи
и имеет в этой точке условный экстремум при условиях связи 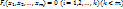 ;2) уравнения
;2) уравнения 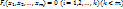 удовлетворяют в некоторой окрестности точки
удовлетворяют в некоторой окрестности точки  условиям теоремы о существовании системы неявных функций
условиям теоремы о существовании системы неявных функций
Теорема о дифференцируемости ф-ии z=f(x,y), заданной неявно ур-ем F(x,y,z)=0. Пусть: 1) функция F(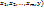 =F(M) дифференцируема в некоторой окрестности W точки Mo(
=F(M) дифференцируема в некоторой окрестности W точки Mo(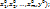 2) частная производная Fy непрерывна в точке
2) частная производная Fy непрерывна в точке  ; 3) F(M0)=0,
; 3) F(M0)=0, 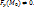 Тогда существует такой параллелепипед
Тогда существует такой параллелепипед  в котором ур-е F(x,y,z)=0 определяет единственную неявную ф-ю y=f(
в котором ур-е F(x,y,z)=0 определяет единственную неявную ф-ю y=f(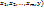 , причем f(
, причем f(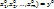 , функция y=f(
, функция y=f(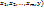 дифференцируема при
дифференцируема при 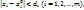 и ее частные производные вычисляются по формуле
и ее частные производные вычисляются по формуле  . (i=1,2,…,m). Тогда существуют числа
. (i=1,2,…,m). Тогда существуют числа 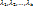 , такие что все частные производные первого порядка функции Лагранжа равны нулю в точке
, такие что все частные производные первого порядка функции Лагранжа равны нулю в точке  .
.
1.3. Функции 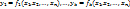 называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция
называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция 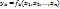 называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде:
называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде: 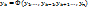 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
1.4. Функции 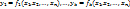 называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция
называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция 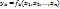 называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде:
называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде: 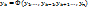 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
2.1. Теорема о существовании и непрерывности ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть 1) ф-я F(x,y) непрерывна в прямоугольнике Q={(x,y):a<x<b, c 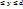 }; 2)
}; 2) 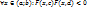 (т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3)
(т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3) 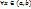 ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
2.2. Теорема о дифференцируемости ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть: 1)ф-я F(x,y) дифференцируема в некоторой окрестности W точки Мо(х0,у0); 2) частная производная Fy непрерывна в точке Мо; 3)F(x0,y0)=0, 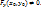 Тогда существует такой прямоугольник
Тогда существует такой прямоугольник 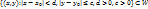 , в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (
, в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (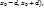 и ее производная вычисляется по формуле
и ее производная вычисляется по формуле 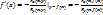 .
.
2.5. Теорема о существовании и дифференцируемости ф-ий y и z, заданных неявно сисемой. Пусть 1)ф-ии F и G, входящие в систему, дифференцируемы в некоторой окрестности W точки 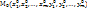 ; 2) частные производные
; 2) частные производные 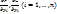 непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0,
непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0, 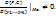 Тогда существует такой параллелепипед
Тогда существует такой параллелепипед  , в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при
, в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при 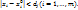
2.6. Теорема о достаточных условиях независимости ф-ии.
Пусть ф-ии 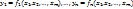 , где n
, где n  m, дифференцируемы в некоторой окрестности
m, дифференцируемы в некоторой окрестности  точки
точки 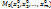 и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в
и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в  .
.
2.7. Теорема о зависимости и независимости ф-ий.
Пусть: 1) ф-ии 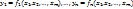 дифференцируемы в окрестности
дифференцируемы в окрестности  точки
точки 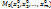 , а частные производные
, а частные производные 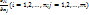 непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий
непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий 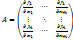 ) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
Тогда r ф-ий, представленных в указанном миноре r-го порядка, независимы в w, а каждая из остальных ф-ий зависит в некоторой окрестности т. М0 от этих r ф-ий.
Тема 10 Поверхностные интегралы
Определение площади поверхностью.
Число S называется пределом сумм 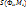 при
при 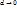 , если
, если 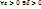 такое, что для любого разбиения поверхности Ф, у которого d<
такое, что для любого разбиения поверхности Ф, у которого d<  , и для любого выбора точек
, и для любого выбора точек  выполняется неравенство |S(
выполняется неравенство |S(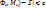 . Если существует
. Если существует 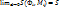 , то поверхность Ф называется квадрируемой, а число S – площадью поверхности Ф.
, то поверхность Ф называется квадрируемой, а число S – площадью поверхности Ф.
1,1 Пусть на квадрируемой поверхности Ф определена функция 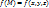 . Разобьем Ф кусочно гладкими кривыми на n квадрируемых частей. На каждой части
. Разобьем Ф кусочно гладкими кривыми на n квадрируемых частей. На каждой части  выберем произвольную точку
выберем произвольную точку  ,и составим интегральную сумму
,и составим интегральную сумму 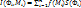 , где
, где 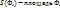 . Пусть
. Пусть 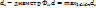 .
.
Число  называется пределом интегральных сумм I(
называется пределом интегральных сумм I(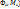 при
при 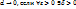 такое, что для любого разбиения Ф, у которого
такое, что для любого разбиения Ф, у которого 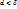 , и для любого выбора точек
, и для любого выбора точек  выполняется неравенство |(
выполняется неравенство |(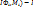 |<
|<  . Предел
. Предел  интегральных сумм называется поверхностным интегралом первого рода от функции
интегральных сумм называется поверхностным интегралом первого рода от функции 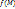 по поверхности Ф и называется
по поверхности Ф и называется 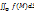 или
или 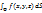
1,2 Если поверхность ограничивает некоторое тело, то у него различают внешнюю и внутреннюю стороны. Примером такой поверхности является сфера. Если поверхность задача уравнением 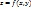 , то у нее различают верхнюю и нижние стороны. Указанные поверхности имеют две стороны. Также существуют односторонние поверхности. Если каждой точке M области G поставлен в соответствие вектор a(M), то говорят, что в области G задано векторное поле. Векторное поле a(M)=
, то у нее различают верхнюю и нижние стороны. Указанные поверхности имеют две стороны. Также существуют односторонние поверхности. Если каждой точке M области G поставлен в соответствие вектор a(M), то говорят, что в области G задано векторное поле. Векторное поле a(M)= 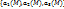 называется непрерывным в области G, если его координаты- функции
называется непрерывным в области G, если его координаты- функции






