Синтез алгоритма управления

Выбор датчиков обратных связей.

- Датчик тока:

Рассчитаем коэффициент усиления датчика тока:

,

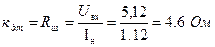где - это максимальное напряжение, которое может пропустить АЦП (для платы L-154).

- Датчик скорости:

В качестве датчика обратной связи по скорости применяют серийно выпускаемые тахогенераторы (ТД-103,ПТ1,ТП11,ТМГ-30). Для нашей системы выберем датчик типа ТД-103.

Коэффициент усиления тахогенератора:

- Датчик положения:

В качестве датчика положения будем использовать потенциометрический датчик типа 2117A50. Коэффициент усиления потенциометрического датчика:

.

 

 

Система дифференциальных уравнений, описывающих объект

Система дифференциальных уравнений, описывающих объект, имеет

следующий вид:

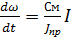
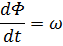
Обозначим ; ;

;

; ;

;

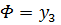
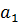= 2.7; = -71.4; = - 1.6; = 3190; = 1

Получим матицы. А и В

Эта система может быть записана в виде , где y – вектор выходных координат, u – вектор управляющих воздействий, B – матрица объекта, A – матрица управляющих воздействий.

Тогда

Определение операторных передаточных функций объекта

 

Согласно формуле для эквивалентной операторной передаточной мат­рицы по управляющим воздействиям получим следующее выражение:

Применительно к рассматриваемой в данном курсовом проекте системе, матрица будет иметь вид:

По полученной формуле определим операторные передаточные функции.

.

Операторные передаточные функции:

ð Время быстродействия T= 0.14

Уравнение параметров состояния

Получим уравнение параметров состояния из исходного дифференциального уравнения объектов.

,

где у(t₁) – вектор начального состояния объекта.

Для дискретной системы, примем и и учтём постоянство вектора управляющего воздействия u на отрезке времени .

После интегрирования получим уравнение параметров состояния:

(k=0,1,2,...), где

;

.

Матрица функции веса W (t):

,

где L ^-1 — оператор обратного преобразования Лапласа.

Матрица W (T) уравнения параметров состояния получается, если приравнять время t периоду дискретности Т, т.е.

.

Синтез алгоритма управления.

Определим минимальное необходимое число шагов дискретности и свободные компоненты управляющего вектора:

где

N – ближайшее большее целое число относительно частного n/l;

n – порядок исходной системы дифференциальных уравнений объекта;

l – размерность вектора управляющих воздействий.

т.е. необходимо иметь 3 шага дискретности.

Далее определим основную матрицу дискретной системы σ_{3 :}

, где

– элементы матрицы ,

Для определения двух других столбцов найдём матрицы и .

Учитывая, что , найдём

,

.

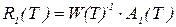Найдем алгоритм дискретного счетно-решающего устройства. Определим матрицу из условия, что датчики производят измерения выходных координат на каждом шаге дискретности.

Найдем элементы первой строки матрицы .

где

.

Для определения элементов матрицы найдем определитель и миноры матрицы .

Алгоритм управления определяется формулой: , где

и