Введем несколько определений.
Определение 3.1. Допустимым решением ( или планом) задачи линейного программирования называется вектор X = (х1, х2,..., хn), удовлетворяющий условиям (3.2) и (3.3).
Другими словами, решение Х=(х1, х2,..., хn) системы уравнений (3.2) называется допустимым, если оно содержит лишь неотрицательные компоненты, то есть, х j ≥ 0 для любых j = 1, n. В противном случае решение называется недопустимым.
Определение 3.2. Допустимым базисным решением ( или опорным планом) системы m линейных уравнений с n переменными называется решение, в котором все n-m свободных (неосновных) переменных равны нулю.
Другими словами,план X = (х1, х2,..., хn) называется опорным, если векторы Ai (i =1,m), входящие в разложение (3.5) с положительными коэффициентами х i, являются линейно независимыми
В задачах ЛП допустимые базисные решения (опорные планы) представляют особый интерес. Совместная система уравнений (3.2) имеет бесконечное множество решений, из них базисных решений – конечное число, не превосходящее 
Определение 3.3. Допустимое базисное решение (опорный план) называется невырожденным, если оно содержит m положительных компонент (то есть, все базисные решения >0), в противном случае допустимое базисное решение называется вырожденным.
Определение 3.4. Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение, обеспечивающее наименьшее (наибольшее) значение целевой функции.
В дальнейшем будем рассматривать решения задач линейного программирования, связанных с нахождением минимального значения целевой функции (если не будет оговорено другое).
Свойства решений задачи линейного программирования тесно связаны со свойствами выпуклых множеств.
Определение 3.5. Точка А, для которой выполняется условие
А = L1·A1 + + L2·A2 +... + Ln·An при Li ≥ 0 (i = 1, n) и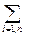 
Li = 1 называется выпуклой линейной комбинацией точек А1, А2,..., Аn
Определение 3.6. Множество точек называется выпуклым, если оно вместе с любыми точками содержит и их произвольную выпуклую комбинацию.
Геометрически смысл этого определения состоит в том, что множеству вместе с его двумя произвольными точками принадлежит и прямолинейный отрезок, их соединяющий.
Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой линейной комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, угловыми точками круга - точки окружности, которая его ограничивает.
Выпуклым многоугольником называется выпуклое замкнутое ограниченноемножество на плоскости, имеющее конечное число угловых точек. Угловые точки многоугольника называются его вершинами, а отрезки, соединяющие две вершины и образующие его границу, - сторонами многоугольника.
Выпуклым многогранником называется замкнутое ограниченное выпуклое множество трехмерного (n-мерного) пространства, имеющее конечное число угловыхточек. Угловые точки многогранника называются его вершинами, а многоугольники, ограничивающие многогранник, - гранями, отрезки, по которым они пересекаются, - ребрами.
