Пояснения к работе.
Математическая статистка изучает методы обработки статистических данных. Под статистическими данными понимают совокупность чисел, полученных в результате опытов, наблюдений, опросов и т.д., количественно характеризующих какой-либо признак (признаки) изучаемых объектов. Множество числовых значений этого признака для всех объектов изучаемой совокупности называют генеральной совокупностью.Выборочной совокупностью (выборкой) называют множество числовых значений признака группы объектов, случайным образом отобранных из всей совокупности рассматриваемых объектов.
Наблюдаемые числовые значения признака называют вариантами. Пусть в выборке, содержащей n элементов, встречаются k разных значений (вариант) некоторого признака: х1, х2,…хк. Количество раз, которое в результате проведения исследований наблюдалась каждая из вариантов, соответственно обозначим n1, n2, …nk. Очевидно, что
n= n1+n2+…+nk.
числа n1, n2, …nk называют частотами, а отношения 
; 
… 
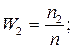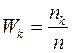- относительными частотами или частостями вариант.
Перечень вариант выборки с указанием соответствующих им частот называется статистическим распределением выборки.
Полигоном частот называют ломаную линию, отрезки которой соединяют точки с координатами (хi, ni).
Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки с координатами (xi,wi). В случае, когда статистическое распределение выборки задано в виде интервалов значений вариант и их частот, геометрическое представление о характере выборки можно получить с помощью гистограмм. Гистограммой частот называют фигуру, состоящую из прямоугольников длиной h, равной величине интервала частот, и высотой 
. Если в качестве высоты прямоугольников рассматривать отношение 
, получим гистограмму относительных частот.
Числовыми характеристиками выборки являются выборочная средняя и выборочная дисперсия.
Рассмотрим выборку, имеющую следующее статистическое распределение:
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
Выборочной средней 
данной выборки назовём среднее арифметическое всех значений xi:
Аналогичным образом для генеральной совокупности со следующим статистическим распределением:
| xi | x1 | x2 | … | xk |
| Ni | N1 | N2 | … | Nk |
определяется генеральная средняя:
Выборная дисперсия Дв вычисляется по формуле:
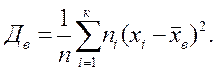
Аналогично определяется генеральная дисперсия Дr:
Решение типовых задач.
Имеется выборка, содержащая 100 числовых значений некоторого признака
По приведённым данным требуется:
а) сгруппировать варианты значений признака по нескольким интервалам и получить таблицу статистического распределения выборки;
б) построить гистограмму частот;
в) считая xi равными значению середины каждого интервала, построить полигон частот, найти выборочную среднюю и выборочную дисперсию.
Решение:
а) Разобьём возможные значения признака на 7 интервалов с шагом h=10, определим для каждого интервала его середину xi и количество ni, попадающих в него вариант.
Результаты запишем в следующую таблицу:
| Интервал | (10;20) | (20;30) | (30;40) | (40;50) | (50;60) | (60;70) | (70;80) |
| xi | |||||||
| ni |
б) По данным, полученным в пункте а, построим гистограмму и полигон частот.
 | |||
 |
в) Найдём выборочную среднюю и выборочную дисперсию: 
= 43,5
(9 (15-43,5)2+14 (25-43,5)2+17 (35-43,5)2+28 (45-43,5)2+ +14 (55-43,5)2+11 (65-43,5)2+7 (75-43,5)2 )= 
Задания для самостоятельного решения.
№1. Выборка задана своим статистическим распределением. Постройте полигон частот и полигон относительных частот, найдите выборочную среднюю и выборочную дисперсию.
а)
| xi | ||||||
| ni |
б)
| xi | ||||||||
| ni |
№2. Имеется выборка, содержащая 50 числовых значений некоторого признака. По приведённым данным требуется:
а) сгруппировать варианты значений признака по нескольким интервалам и получить таблицу статистического распределения выборки;
б) построить гистограмму частот;
в) считая xi равными значению середины каждого интервала, построить полигон частот, найти выборочную среднюю и выборочную дисперсию.
а)
б)
в)
