Показательное распределение

Министерство образования Тверской области

Тверской колледж имени А.Н. Коняева

Доклад

По дисциплине:

Теория вероятностей и математическая статистика

На тему:

«Случайные величины»

Выполнил (а) студент группы 2ПР

Голубев И.А

Проверил преподаватель

Тверь

Содержание

1.Теоретическая часть ……………………………………………………….3-13

2.Список использованной литературы ………………………………………14

Теоретическая часть

Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений.
В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д.
Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.
Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.
Различают дискретные и непрерывные случайные величины.
Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной.
Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной.
Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.
Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:

Х	х ₁	х ₂	…	х_n	∑
Р	р ₁	р ₂	…	р_n

Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х ₁, х ₂, …, х_n. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = х_i (i = 1, 2, …, n) образуют полную группу попарно независимых событий. Следовательно, р ₁ + р ₂ + … + р_n = 1.
Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения.

Функция распределения вероятностей
Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.
F(x) = P (X < x).
Иногда функцию F(x) называют интегральной функцией распределения.
Функция распределения обладает следующими свойствами:
1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1
2. Функции распределения есть неубывающая функция.
3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале: Р(а < X < b) = F(b) – F(а).
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то F(x) = 0 при х ≤ а ; F(x) = 1 при х ≥ b.
5. Справедливы следующие предельные отношения:

Для дискретной случайной величины Х, которая может принимать значения х ₁, х ₂, …, х_n, функция распределения имеет вид
F(x)=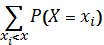
где неравенство под знаком суммы означает, что суммирование касается всех тех значений х_i, величина которых меньше х.
Поясним эту формулу исходя из определения функции F(x). Предположим, что аргумент х принял какое-то определенное, но такое, что выполняется неравенство x_i < x ≤ x_i ₊₁. Тогда левее числа х на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1, 2, 3, …, i. Поэтому неравенство Х < x выполняется, если величина Х примет значения х_к, где k = 1, 2, …, i. Таким образом, событие Х < x наступит, если наступит любое, неважно какое, из событий Х = х ₁, Х = х ₂, Х = х ₃, …, Х = х_i. Так как эти события несовместны, то по теореме сложения вероятностей имеем
P(X< x) = P(X= )+P(X= )+…+ P(X= ) =
Предположим теперь, что для непрерывной случайной величины Х ее функция распределения F(x) имеет непрерывную производную
F'(x)= φ(x).
Функцию φ(x) называют плотностью вероятности (для данного распределения) или дифференциальной функцией.
Так как плотность вероятности φ(x) является производной неубывающей функции F(x), то она неотрицательна: φ(x)≥0. В отличие от функции распределения, плотность вероятности может принимать сколь угодно большие значения.
Так как F(x) является первообразной для φ(x), то на основании формулы Ньютона-Лейбница имеем . Отсюда получаем
P(a ≤ X ≤ b) =
Полагая а = –∞ и b = +∞, получаем достоверное событие Х принадлежащее (–∞, +∞), вероятность которого равна единице. Следовательно,

В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то . Полагая в формуле а = –∞, b = х и обозначая для ясности переменную интегрирования t, получим функцию распределения:
F(x) = P (– ∞ < X < x) = .
Числовые характеристики случайной величины

Функция распределения содержит полную информацию о случайной величине. На практике функцию распределения не всегда можно установить; иногда такого исчерпывающего знания и не требуется. Частичную информацию о случайной величине дают числовые характеристики, которые в зависимости от рода информации делятся на следующие группы.
1. Характеристики положения случайной величины на числовой оси (мода Мo, медиана Мe, математическое ожидание М(Х)).
2. Характеристики разброса случайной величины около среднего значения (дисперсия D(X), среднее квадратическое отклонение σ(х)).
3. Характеристики формы кривой y = φ(x) (асимметрия As, эксцесс Ех).
Рассмотрим подробнее каждую из указанных характеристик.
Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений:
M(X)=
Для непрерывной случайной величины Х, имеющей заданную плотность распределения φ(x) математическим ожиданием называется следующий интеграл:
M(X)=
Здесь предполагается, что несобственный интеграл:

сходится абсолютно, т.е. существует.
Свойства математического ожидания:
1. М(С) = C, где С = const;
2. M(C ∙ Х) = С ∙ М(Х);
3. М(Х ± Y) = М(Х) ± М(Y), где X и Y – любые случайные величины;
4. М(Х ∙ Y)= М(Х)∙ М(Y), где X и Y – независимые случайные величины.
Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.
Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис. 2.3), а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис. 2.4).

Рис. 2.3 Рис. 2.4
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.
Р(Х < Ме) = Р(X > Ме)
Из определения медианы следует, что Р(Х < Ме) = 0,5, т.е. F (Ме) = 0,5. Геометрически медиану можно истолковывать как абсциссу, в которой ордината φ(x) делит пополам площадь, ограниченную кривой распределения (рис. 2.5). В случае симметричного распределения медиана совпадает с модой и математическим ожиданием (рис. 2.6).

Рис. 2.5 Рис. 2.6
Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания.
D(X) = M(X – М(Х))².
Дисперсию случайной величины Х удобно вычислять по формуле:
а) для дискретной величины
D(X)=M(;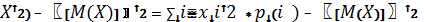
б) для непрерывной случайной величины
D(X) = f(х)d x – [M(X)]².
Дисперсия обладает следующими свойствами:
1. D(C) = 0, где С = const;
2. D(C × X) = C²∙ D(X);
3. D (X ± Y) = D (X) + D (Y), если X и Y независимые случайные величины.
Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е.
σ(X) = .

Обобщением основных числовых характеристик случайных величин является понятие моментов случайной величины.
Начальным моментом k-го порядка α _k случайной величины Х называется математическое ожидание величины Х^k, т.е. α _k = М(Х^k).
Начальный момент первого порядка – это математическое ожидание случайной величины.
Центральным моментом k-го порядка μ _k случайной величины Х называется математическое ожидание величины (Х – М(Х)) ^k, т.е. μ _k = М(Х – М(Х)) ^k.
Центральный момент второго порядка – это дисперсия случайной величины.
Для дискретной случайной величины начальный момент выражается суммой α _k = , а центральный – суммой μ _k = , где р_i = p(X = x_i). Для начального и центрального моментов непрерывной случайной величины можно получить следующие равенства:
α _k = , μ _k = ,
где φ(x) – плотность распределения случайной величины Х.
Величина As = μ₃ / σ³ называется коэффициентом асимметрии.
Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину m₃ отрицательных отклонений. В этом случае кривая распределения (рис.2.7) более полога слева от М(Х). Если коэффициент As положительный, а значит, преобладает влияние положительных отклонений, то кривая распределения (рис.2.7) более полога справа. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции).

Рис. 2.7
Эксцессом Еk называется величина
Еk = μ₄ / σ⁴ – 3.
Можно показать, что для наиболее распространенного в природе нормального закона распределения, который будет рассматриваться в следующем параграфе, отношение μ₄ / σ⁴ = 3. Поэтому эксцесс служит для сравнения данного распределения с нормальным, у которого эксцесс равен нулю. Можно было бы доказать, что распределения более островершинные, чем нормальное, имеют эксцесс Еk > 0, а более плосковершинные – имеют эксцесс Еk < 0 (рис.3.8).

Рис. 2.8

Биномиальное распределение

Пусть в каждом из n независимых испытаний событие А может произойти с одной и той же вероятностью р (следовательно, вероятность непоявления q =1 – p). Дискретная случайная величина Х – число наступлений события А – имеет распределение, которое называется биномиальным.
Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: х ₁ = 0, х ₂ = 1, х ₃ = 2,…, х_n ₊₁ = n. Вероятность возможного значения Х = k (числа k появления события) вычисляют по формуле Бернулли:
P_n(k) = C _n^k · p^k · qⁿ ^{– k},
где k = 0, 1, 2, …, n.
Ряд распределения случайной величины Х, подчиненной биномиальному закону, можно представить в виде следующей таблицы:

Х			…	K	…	n
Р	C_n ⁰· p ⁰· qⁿ	C_n ¹ · p ¹· qⁿ ^–1	…	C_n^k · p^k · q^n–k	…	C_nⁿ · pⁿ · q ⁰

Название закона связао с тем, что вероятности P_n (k) при k = 0, 1, 2, …, n являются членами разложения бинома Ньютона
(p + q)ⁿ = qⁿ + C_n ¹· p ¹· qⁿ ^–1 + … + C_n^k · p^k · qⁿ ^{– k} + … + pⁿ.

Отсюда сразу видно, что сумма всех вероятностей второй строки таблицы равна 1, так как p + q =1.

Равномерное распределение

Непрерывная случайная величина Х имеет равномерное распределение на отрезке [ a, b ], если ее плотность имеет следующий вид:

График плотности распределения показан на рис. 2.9.

φ(х)

Рис. 2.9
Найдем значение постоянной С. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда С = 1/(b – a).
Пусть [ α, β ] Ì [ a, b ]. Тогда, p=P( т.е.
,
где L – длина (линейная мера) всего отрезка [ a, b ] и l – длина частичного отрезка [ α, β].
Значения случайной величины Х, т.е. точки х отрезка [ a, b ], можно рассматривать как всевозможные элементарные исходы некоторого испытания. Пусть событие А состоит в том, что результат испытания принадлежит отрезку [ α, β] Ì [ a, b ]. Тогда точки отрезка [ α, β] есть благоприятные элементарные исходы события А.
Согласно формуле имеем геометрическое определение вероятности: под вероятностью события А понимается отношение меры множества элементарных исходов, благоприятствующих событию А, к мере L множества всех возможных элементарных исходов в предположении, что они равновозможны:
.
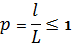Это определение естественно переносит классическое определение вероятности на случай бесконечного числа элементарных исходов (случаев).
Аналогичное определение можно ввести также тогда, когда элементарные исходы испытания представляют собой точки плоскости или пространства.

Показательное распределение

Непрерывная случайная величина Х, функция плотности которой задается выражением

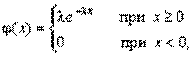
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. Здесь параметр λ постоянная положительная величина.
Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Также этому распределению подчиняется время ожидания клиента в системе массового обслуживания (магазин, мастерская, банк, парикмахерская и т.д.). Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению. График дифференциальной функции показательного распределения показан на рис. 2.11.

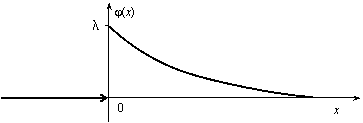
Рис. 2.11

Нормальное распределение

Случайная величина Х имеет нормальное распределение (или распределение по закону Гаусса), если ее плотность вероятности имеет вид:
,
где параметры а – любое действительное число и σ >0.
График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса). Нормальная кривая (рис. 2.12) симметрична относительно прямой х = а, имеет максимальную ординату , а в точках х = а ± σ – перегиб.

Рис. 2.12
Доказано, что параметр а является математическим ожиданием (также модой и медианой), а σ – средним квадратическим отклонением. Коэффициенты асимметрии и эксцесса для нормального распределения равны нулю: As = Ex = 0.
Установим теперь, как влияет изменение параметров а и σ на вид нормальной кривой. При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо (рис. 2.13).
При изменении параметра σ изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение функции убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра σ кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением σ кривая стягивается к прямой х = а (рис. 2.14).

Рис. 2.13 Рис. 2.14
Функция плотности нормального распределения φ(х) с параметрами а = 0, σ = 1 называется плотностью стандартной нормальной случайной величины, а ее график – стандартной кривой Гаусса.
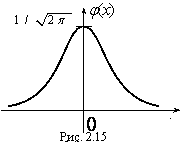Функция плотности нормальной стандартной величины определяется формулой 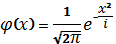, а ее график изображен на рис. 2.15.
Из свойств математического ожидания и дисперсии следует, что для величины U= , D(U)=1, M (U) = 0. Поэтому стандартную нормальную кривую можно рассматривать как кривую распределения случайной величины U= ,

где Х – случайная величина, подчиненная нормальному закону распределения с параметрами а и σ.
Нормальный закон распределения случайной величины в интегральной форме имеет вид
F(x) =
Для случайной величины Х, подчиняющейся нормальному закону, вероятность ее попадания на отрезок [ α, β] есть

Нормальное распределение имеет ряд свойств, делающих его одним из самых употребительных в статистике распределений.
Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой независимости). Также ни одна из суммируемых случайных величин не должна резко отличаться от других, т.е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию.
Этим и объясняется широкая распространенность нормального распределения. Оно возникает во всех явлениях, процессах, где рассеяния случайной изучаемой величины вызывается большим количеством случайных причин, влияние каждой из которых в отдельности на рассеяние ничтожно мало.